Analysis of algorithms | little o and little omega notations
Last Updated :
22 Mar, 2024
The main idea of asymptotic analysis is to have a measure of the efficiency of algorithms that don’t depend on machine-specific constants, mainly because this analysis doesn’t require algorithms to be implemented and time taken by programs to be compared. We have already discussed Three main asymptotic notations. The following 2 more asymptotic notations are used to represent the time complexity of algorithms.
Little o Asymptotic Notation:
Big O is used as a tight upper bound on the growth of an algorithm’s effort (this effort is described by the function f(n)), even though, as written, it can also be a loose upper bound. “Little o” (o) notation is used to describe an upper bound that cannot be tight.
In the domain of algorithm analysis, the little o notation is a valuable tool used to describe the behavior of functions as they approach certain limits. When we say that a function f(n) is o(g(n)), we are essentially stating that f(n) grows slower than g(n) as n approaches infinity. In simpler terms, if f(n) = o(g(n)), it means that g(n) grows faster than f(n).
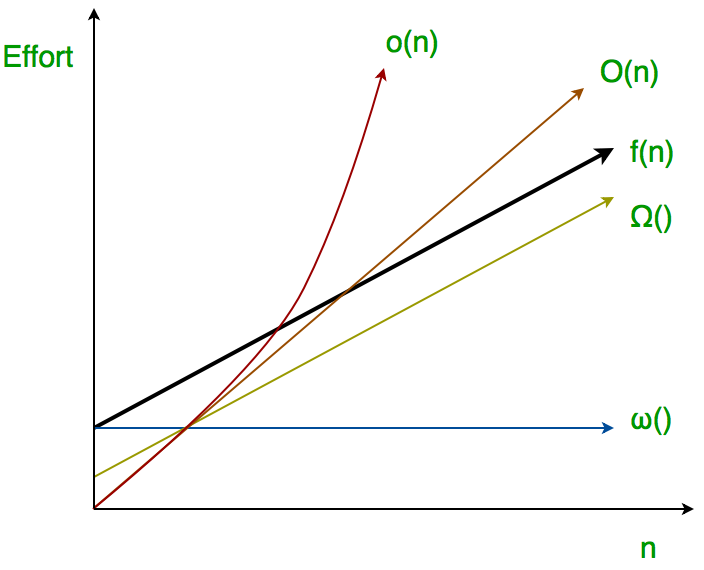
Thus, Little o means loose upper-bound of f(n). Little o is a rough estimate of the maximum order of growth whereas Big-O may be the actual order of growth.
Mathematical Relation:
f(n) = o(g(n)) means lim f(n)/g(n) = 0 n→∞
Examples:
Is 7n + 8 ∈ o(n2)
In order for that to be true, for any c, we have to be able to find an n0 that makes f(n) < c * g(n) asymptotically true.
lets took some example,
If c = 100,we check the inequality is clearly true. If c = 1/100 , we’ll have to use a little more imagination, but we’ll be able to find an n0. (Try n0 = 1000.) From these examples, the conjecture appears to be correct.
then check limits,
lim f(n)/g(n) = lim (7n + 8)/(n2) = lim 7/2n = 0 (l’hospital)
n→∞ n→∞ n→∞
hence 7n+8 ∈ o(n2)
Little ω Asymptotic Notation:
On the other hand, little ω notation is used to describe the relationship between two functions when one grows strictly faster than the other. If a function f(n) is ω(g(n)), it means that g(n) grows slower than f(n) as n approaches infinity.
f(n) has a higher growth rate than g(n) so main difference between Big Omega (Ω) and Little omega (ω) lies in their definitions.In the case of Big Omega f(n)=ω(g(n)) and the bound is 0<=cg(n)<=f(n), but in case of little omega, it is true for 0<=c*g(n)<f(n).
The relationship between Big Omega (Ω) and Little Omega (ω) is similar to that of Big-O and Little o except that now we are looking at the lower bounds. Little Omega (ω) is a rough estimate of the order of the growth whereas Big Omega (Ω) may represent exact order of growth. We use notation to denote a lower bound that is not asymptotically tight, and f(n) ∈ ω(g(n)) if and only if g(n) ∈ ο((f(n)).
Mathmatical Relation:
if f(n) ∈ ω(g(n)) then, lim f(n)/g(n) = ∞ n→∞
Example:
Prove that 4n+6 ∈ ο(1);
The little omega(ο) running time can be proven by applying limit formula given below.
if lim f(n)/g(n) = ∞ then functions f(n) is ο(g(n))
n→∞
here,we have functions f(n)=4n+6 and g(n)=1
lim (4n+6)/(1) = ∞
n→∞ and,also for any c we can get n0 for this inequality 0<=c*g(n)<f(n) ,
0<=c*1<4n+6. So,hence proved.
Conclusion:
In conclusion, little o and little ω notations are essential tools in algorithm analysis that allow us to compare the growth rates of functions in a precise manner. By understanding these notations, we can better analyze and predict the performance of algorithms as their input sizes grow.
Share your thoughts in the comments
Please Login to comment...