Complexity of different operations in Binary tree, Binary Search Tree and AVL tree
Last Updated :
21 Dec, 2022
In this article, we will discuss the complexity of different operations in binary trees including BST and AVL trees. Before understanding this article, you should have a basic idea about Binary Tree, Binary Search Tree, and AVL Tree. The main operations in a binary tree are: search, insert and delete. We will see the worst-case time complexity of these operations in binary trees:
Binary Tree:
In a binary tree, a node can have maximum of two children. Consider the left-skewed binary tree shown in Figure 1:
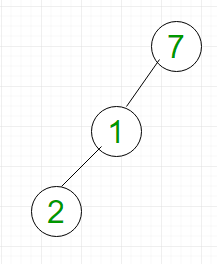
Complexity Analysis:
- Searching: For searching element 2, we have to traverse all elements (assuming we do breadth first traversal). Therefore, searching in binary tree has worst case complexity of O(N).
- Insertion: For inserting element as left child of 2, we have to traverse all elements. Therefore, insertion in binary tree has worst case complexity of O(N).
- Deletion: For deletion of element 2, we have to traverse all elements to find 2 (assuming we do breadth first traversal). Therefore, deletion in binary tree has worst case complexity of O(N).
Binary Search Tree (BST):
BST is a special type of binary tree in which the left child of a node has a value less than the parent and the right child has a value greater than the parent. Consider the left-skewed BST shown in Figure 2.
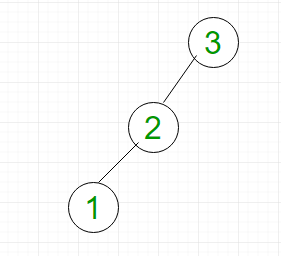
Complexity Analysis:
- Searching: For searching element 1, we have to traverse all elements (in order 3, 2, 1). Therefore, searching in binary search tree has worst case complexity of O(n). In general, the time complexity is O(h) where h is the height of BST.
- Insertion: For inserting element 0, it must be inserted as the left child of 1. Therefore, we need to traverse all elements (in order 3, 2, 1) to insert 0 which has the worst-case complexity of O(n). In general, the time complexity is O(h).
- Deletion: For deletion of element 1, we have to traverse all elements to find 1 (in order 3, 2, 1). Therefore, deletion in binary tree has worst case complexity of O(n). In general, the time complexity is O(h).
AVL/ Height Balanced Tree:
AVL tree is a binary search tree with an additional property that the difference between the height of the left sub-tree and the right sub-tree of any node can’t be more than 1
For example, BST shown in Figure 2 is not AVL as the difference between the left sub-tree and the right sub-tree of node 3 is 2. However, BST shown in Figure 3 is an AVL tree
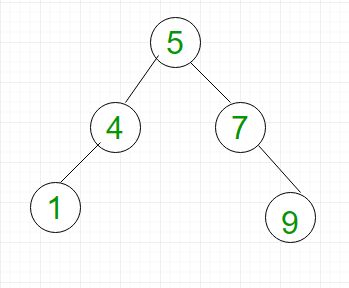
Complexity Analysis:
- Searching: For searching element 1, we have to traverse elements (in order 5, 4, 1) = 3 = log2n. Therefore, searching in the AVL tree has worst-case complexity of O(log2n).
- Insertion: For inserting element 12, it must be inserted as the right child of 9. Therefore, we need to traverse elements (in order 5, 7, 9) to insert 12 which has the worst-case complexity of O(log2n).
- Deletion: For deletion of element 9, we have to traverse elements to find 9 (in order 5, 7, 9). Therefore, deletion in a binary tree has worst-case complexity of O(log2n).
We will discuss questions based on the complexities of binary tree operations:
Que-1. What is the worst-case time complexity for search, insert and delete operations in a general Binary Search Tree?
- (A) O(n) for all
- (B) O(Logn) for all
- (C) O(Logn) for search and insert, and O(n) for delete
- (D) O(Logn) for search, and O(n) for insert and delete
Solution: As discussed, all operations in BST have the worst-case time complexity of O(n). So, the correct option is (A).
Que-2. What are the worst-case time complexities of searching in a binary tree, BST, and AVL tree respectively?
- (A) O(n) for all
- (B) O(Logn) for all
- (C) O(n) for binary tree, and O(Logn) for others
- (D) O(n) for binary tree and BST, and O(Logn) for AVL
Solution: As discussed, search operation in binary tree and BST have worst-case time complexity of O(n). However, the AVL tree has the worst-case time complexity of O(log n). So, the correct option is (D).
Share your thoughts in the comments
Please Login to comment...