Nth Fibonacci Number
Last Updated :
03 Oct, 2023
Given a number n, print n-th Fibonacci Number.
The Fibonacci numbers are the numbers in the following integer sequence: 0, 1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89, 144, ……..

Examples:
Input : n = 1
Output : 1
Input : n = 9
Output : 34
Input : n = 10
Output : 55
[/Tex]
with seed values and 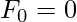 and
and 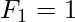 .
.
C++
#include <bits/stdc++.h>
using namespace std;
int fib(int n)
{
int a = 0, b = 1, c, i;
if (n == 0)
return a;
for (i = 2; i <= n; i++) {
c = a + b;
a = b;
b = c;
}
return b;
}
int main()
{
int n = 9;
cout << fib(n);
return 0;
}
|
C
#include <stdio.h>
int fib(int n)
{
int a = 0, b = 1, c, i;
if (n == 0)
return a;
for (i = 2; i <= n; i++) {
c = a + b;
a = b;
b = c;
}
return b;
}
int main()
{
int n = 9;
printf("%d", fib(n));
getchar();
return 0;
}
|
Java
public class fibonacci {
static int fib(int n)
{
int a = 0, b = 1, c;
if (n == 0)
return a;
for (int i = 2; i <= n; i++) {
c = a + b;
a = b;
b = c;
}
return b;
}
public static void main(String args[])
{
int n = 9;
System.out.println(fib(n));
}
};
|
Python3
def fibonacci(n):
a = 0
b = 1
if n < 0:
print("Incorrect input")
elif n == 0:
return a
elif n == 1:
return b
else:
for i in range(2, n+1):
c = a + b
a = b
b = c
return b
print(fibonacci(9))
|
C#
using System;
namespace Fib {
public class GFG {
static int Fib(int n)
{
int a = 0, b = 1, c = 0;
if (n == 0)
return a;
for (int i = 2; i <= n; i++) {
c = a + b;
a = b;
b = c;
}
return b;
}
public static void Main(string[] args)
{
int n = 9;
Console.Write("{0} ", Fib(n));
}
}
}
|
Javascript
<script>
function fib(n)
{
let a = 0, b = 1, c, i;
if( n == 0)
return a;
for(i = 2; i <= n; i++)
{
c = a + b;
a = b;
b = c;
}
return b;
}
let n = 9;
document.write(fib(n));
</script>
|
PHP
<?php
function fib( $n)
{
$a = 0;
$b = 1;
$c;
$i;
if( $n == 0)
return $a;
for($i = 2; $i <= $n; $i++)
{
$c = $a + $b;
$a = $b;
$b = $c;
}
return $b;
}
$n = 9;
echo fib($n);
?>
|
Time Complexity: O(n)
Auxiliary Space: O(1)
Recursion Approach to Find and Print Nth Fibonacci Numbers:
In mathematical terms, the sequence Fn of Fibonacci numbers is defined by the recurrence relation: 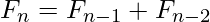 with seed values and
with seed values and 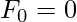 and
and 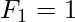 .
.
The Nth Fibonacci Number can be found using the recurrence relation shown above:
- if n = 0, then return 0.
- If n = 1, then it should return 1.
- For n > 1, it should return Fn-1 + Fn-2
Below is the implementation of the above approach:
C++
#include <bits/stdc++.h>
using namespace std;
int fib(int n)
{
if (n <= 1)
return n;
return fib(n - 1) + fib(n - 2);
}
int main()
{
int n = 9;
cout << n << "th Fibonacci Number: " << fib(n);
return 0;
}
|
C
#include <stdio.h>
int fib(int n)
{
if (n <= 1)
return n;
return fib(n - 1) + fib(n - 2);
}
int main()
{
int n = 9;
printf("%dth Fibonacci Number: %d", n, fib(n));
return 0;
}
|
Java
import java.io.*;
class fibonacci {
static int fib(int n)
{
if (n <= 1)
return n;
return fib(n - 1) + fib(n - 2);
}
public static void main(String args[])
{
int n = 9;
System.out.println(
n + "th Fibonacci Number: " + fib(n));
}
}
|
Python3
def fibonacci(n):
if n <= 1:
return n
return fibonacci(n-1) + fibonacci(n-2)
if __name__ == "__main__":
n = 9
print(n, "th Fibonacci Number: ")
print(fibonacci(n))
|
C#
using System;
public class GFG {
public static int Fib(int n)
{
if (n <= 1) {
return n;
}
else {
return Fib(n - 1) + Fib(n - 2);
}
}
public static void Main(string[] args)
{
int n = 9;
Console.Write(n + "th Fibonacci Number: " + Fib(n));
}
}
|
Javascript
function Fib(n) {
if (n <= 1) {
return n;
} else {
return Fib(n - 1) + Fib(n - 2);
}
}
let n = 9;
console.log(n + "th Fibonacci Number: " + Fib(n));
|
PHP
<?php
function Fib($n)
{
if ($n <= 1) {
return $n;
}
else {
return Fib($n - 1) + Fib($n - 2);
}
}
$n = 9;
echo $n . "th Fibonacci Number: " . Fib($n);
?>
|
Time Complexity: Exponential, as every function calls two other functions.
Auxiliary space complexity: O(n), as the maximum depth of the recursion tree is n.
Dynamic Programming Approach to Find and Print Nth Fibonacci Numbers:
Consider the Recursion Tree for the 5th Fibonacci Number from the above approach:
fib(5)
/ \
fib(4) fib(3)
/ \ / \
fib(3) fib(2) fib(2) fib(1)
/ \ / \ / \
fib(2) fib(1) fib(1) fib(0) fib(1) fib(0)
/ \
fib(1) fib(0)
If you see, the same method call is being done multiple times for the same value. This can be optimized with the help of Dynamic Programming. We can avoid the repeated work done in the Recursion approach by storing the Fibonacci numbers calculated so far.
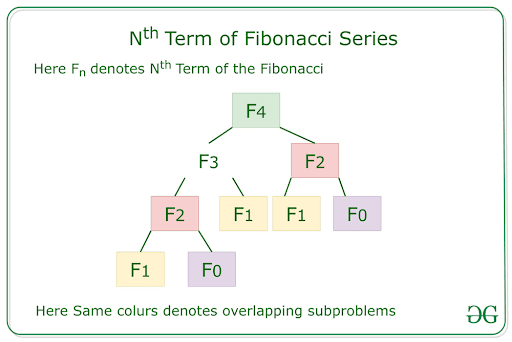
Dynamic Programming Approach to Find and Print Nth Fibonacci Numbers:
Below is the implementation of the above approach:
C++
#include <bits/stdc++.h>
using namespace std;
class GFG {
public:
int fib(int n)
{
int f[n + 2];
int i;
f[0] = 0;
f[1] = 1;
for (i = 2; i <= n; i++) {
f[i] = f[i - 1] + f[i - 2];
}
return f[n];
}
};
int main()
{
GFG g;
int n = 9;
cout << g.fib(n);
return 0;
}
|
C
#include <stdio.h>
int fib(int n)
{
int f[n + 2];
int i;
f[0] = 0;
f[1] = 1;
for (i = 2; i <= n; i++) {
f[i] = f[i - 1] + f[i - 2];
}
return f[n];
}
int main()
{
int n = 9;
printf("%d", fib(n));
getchar();
return 0;
}
|
Java
public class fibonacci {
static int fib(int n)
{
int f[]
= new int[n
+ 2];
int i;
f[0] = 0;
f[1] = 1;
for (i = 2; i <= n; i++) {
f[i] = f[i - 1] + f[i - 2];
}
return f[n];
}
public static void main(String args[])
{
int n = 9;
System.out.println(fib(n));
}
};
|
Python3
def fibonacci(n):
f = [0, 1]
for i in range(2, n+1):
f.append(f[i-1] + f[i-2])
return f[n]
print(fibonacci(9))
|
C#
using System;
class fibonacci {
static int fib(int n)
{
int[] f = new int[n + 2];
int i;
f[0] = 0;
f[1] = 1;
for (i = 2; i <= n; i++) {
f[i] = f[i - 1] + f[i - 2];
}
return f[n];
}
public static void Main()
{
int n = 9;
Console.WriteLine(fib(n));
}
}
|
Javascript
<script>
function fib(n)
{
let f = new Array(n+2);
let i;
f[0] = 0;
f[1] = 1;
for (i = 2; i <= n; i++)
{
f[i] = f[i-1] + f[i-2];
}
return f[n];
}
let n=9;
document.write(fib(n));
</script>
|
PHP
<?php
function fib( $n)
{
$f = array();
$i;
$f[0] = 0;
$f[1] = 1;
for ($i = 2; $i <= $n; $i++)
{
$f[$i] = $f[$i-1] + $f[$i-2];
}
return $f[$n];
}
$n = 9;
echo fib($n);
?>
|
Time complexity: O(n) for given n
Auxiliary space: O(n)
Nth Power of Matrix Approach to Find and Print Nth Fibonacci Numbers
This approach relies on the fact that if we n times multiply the matrix M = {{1,1},{1,0}} to itself (in other words calculate power(M, n)), then we get the (n+1)th Fibonacci number as the element at row and column (0, 0) in the resultant matrix.
- If n is even then k = n/2:
- Therefore Nth Fibonacci Number = F(n) = [2*F(k-1) + F(k)]*F(k)
- If n is odd then k = (n + 1)/2:
- Therefore Nth Fibonacci Number = F(n) = F(k)*F(k) + F(k-1)*F(k-1)
How does this formula work?
The formula can be derived from the matrix equation.
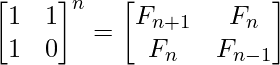
Taking determinant on both sides, we get (-1)n = Fn+1Fn-1 – Fn2
Moreover, since AnAm = An+m for any square matrix A, the following identities can be derived (they are obtained from two different coefficients of the matrix product)
FmFn + Fm-1Fn-1 = Fm+n-1 —————————(1)
By putting n = n+1 in equation(1),
FmFn+1 + Fm-1Fn = Fm+n ————————–(2)
Putting m = n in equation(1).
F2n-1 = Fn2 + Fn-12
Putting m = n in equation(2)
F2n = (Fn-1 + Fn+1)Fn = (2Fn-1 + Fn)Fn ——–
( By putting Fn+1 = Fn + Fn-1 )
To get the formula to be proved, we simply need to do the following
- If n is even, we can put k = n/2
- If n is odd, we can put k = (n+1)/2
Below is the implementation of the above approach
C++
#include <bits/stdc++.h>
using namespace std;
void multiply(int F[2][2], int M[2][2]);
void power(int F[2][2], int n);
int fib(int n)
{
int F[2][2] = { { 1, 1 }, { 1, 0 } };
if (n == 0)
return 0;
power(F, n - 1);
return F[0][0];
}
void power(int F[2][2], int n)
{
if (n == 0 || n == 1)
return;
int M[2][2] = { { 1, 1 }, { 1, 0 } };
power(F, n / 2);
multiply(F, F);
if (n % 2 != 0)
multiply(F, M);
}
void multiply(int F[2][2], int M[2][2])
{
int x = F[0][0] * M[0][0] + F[0][1] * M[1][0];
int y = F[0][0] * M[0][1] + F[0][1] * M[1][1];
int z = F[1][0] * M[0][0] + F[1][1] * M[1][0];
int w = F[1][0] * M[0][1] + F[1][1] * M[1][1];
F[0][0] = x;
F[0][1] = y;
F[1][0] = z;
F[1][1] = w;
}
int main()
{
int n = 9;
cout << fib(9);
getchar();
return 0;
}
|
C
#include <stdio.h>
void multiply(int F[2][2], int M[2][2]);
void power(int F[2][2], int n);
int fib(int n)
{
int F[2][2] = { { 1, 1 }, { 1, 0 } };
if (n == 0)
return 0;
power(F, n - 1);
return F[0][0];
}
void power(int F[2][2], int n)
{
if (n == 0 || n == 1)
return;
int M[2][2] = { { 1, 1 }, { 1, 0 } };
power(F, n / 2);
multiply(F, F);
if (n % 2 != 0)
multiply(F, M);
}
void multiply(int F[2][2], int M[2][2])
{
int x = F[0][0] * M[0][0] + F[0][1] * M[1][0];
int y = F[0][0] * M[0][1] + F[0][1] * M[1][1];
int z = F[1][0] * M[0][0] + F[1][1] * M[1][0];
int w = F[1][0] * M[0][1] + F[1][1] * M[1][1];
F[0][0] = x;
F[0][1] = y;
F[1][0] = z;
F[1][1] = w;
}
int main()
{
int n = 9;
printf("%d", fib(9));
getchar();
return 0;
}
|
Java
public class fibonacci {
static int fib(int n)
{
int F[][] = new int[][] { { 1, 1 }, { 1, 0 } };
if (n == 0)
return 0;
power(F, n - 1);
return F[0][0];
}
static void multiply(int F[][], int M[][])
{
int x = F[0][0] * M[0][0] + F[0][1] * M[1][0];
int y = F[0][0] * M[0][1] + F[0][1] * M[1][1];
int z = F[1][0] * M[0][0] + F[1][1] * M[1][0];
int w = F[1][0] * M[0][1] + F[1][1] * M[1][1];
F[0][0] = x;
F[0][1] = y;
F[1][0] = z;
F[1][1] = w;
}
static void power(int F[][], int n)
{
if (n == 0 || n == 1)
return;
int M[][] = new int[][] { { 1, 1 }, { 1, 0 } };
power(F, n / 2);
multiply(F, F);
if (n % 2 != 0)
multiply(F, M);
}
public static void main(String args[])
{
int n = 9;
System.out.println(fib(n));
}
};
|
Python3
def fib(n):
F = [[1, 1],
[1, 0]]
if (n == 0):
return 0
power(F, n - 1)
return F[0][0]
def multiply(F, M):
x = (F[0][0] * M[0][0] +
F[0][1] * M[1][0])
y = (F[0][0] * M[0][1] +
F[0][1] * M[1][1])
z = (F[1][0] * M[0][0] +
F[1][1] * M[1][0])
w = (F[1][0] * M[0][1] +
F[1][1] * M[1][1])
F[0][0] = x
F[0][1] = y
F[1][0] = z
F[1][1] = w
def power(F, n):
if(n == 0 or n == 1):
return
M = [[1, 1],
[1, 0]]
power(F, n // 2)
multiply(F, F)
if (n % 2 != 0):
multiply(F, M)
if __name__ == "__main__":
n = 9
print(fib(n))
|
C#
using System;
class GFG {
static int fib(int n)
{
int[, ] F = new int[, ] { { 1, 1 }, { 1, 0 } };
if (n == 0)
return 0;
power(F, n - 1);
return F[0, 0];
}
static void multiply(int[, ] F, int[, ] M)
{
int x = F[0, 0] * M[0, 0] + F[0, 1] * M[1, 0];
int y = F[0, 0] * M[0, 1] + F[0, 1] * M[1, 1];
int z = F[1, 0] * M[0, 0] + F[1, 1] * M[1, 0];
int w = F[1, 0] * M[0, 1] + F[1, 1] * M[1, 1];
F[0, 0] = x;
F[0, 1] = y;
F[1, 0] = z;
F[1, 1] = w;
}
static void power(int[, ] F, int n)
{
if (n == 0 || n == 1)
return;
int[, ] M = new int[, ] { { 1, 1 }, { 1, 0 } };
power(F, n / 2);
multiply(F, F);
if (n % 2 != 0)
multiply(F, M);
}
public static void Main()
{
int n = 9;
Console.Write(fib(n));
}
}
|
Javascript
<script>
function fib(n)
{
var F = [ [ 1, 1 ], [ 1, 0 ] ];
if (n == 0)
return 0;
power(F, n - 1);
return F[0][0];
}
function multiply(F, M)
{
var x = F[0][0] * M[0][0] + F[0][1] * M[1][0];
var y = F[0][0] * M[0][1] + F[0][1] * M[1][1];
var z = F[1][0] * M[0][0] + F[1][1] * M[1][0];
var w = F[1][0] * M[0][1] + F[1][1] * M[1][1];
F[0][0] = x;
F[0][1] = y;
F[1][0] = z;
F[1][1] = w;
}
function power(F, n)
{
if (n == 0 || n == 1)
return;
var M = [ [ 1, 1 ], [ 1, 0 ] ];
power(F, n / 2);
multiply(F, F);
if (n % 2 != 0)
multiply(F, M);
}
var n = 9;
document.write(fib(n));
</script>
|
Time Complexity: O(Log n)
Auxiliary Space: O(Log n) if we consider the function call stack size, otherwise O(1).
Related Articles:
Large Fibonacci Numbers in Java
Share your thoughts in the comments
Please Login to comment...