2-3 Trees | (Search, Insert and Deletion)
Last Updated :
05 Sep, 2022
In binary search trees we have seen the average-case time for operations like search/insert/delete is O(log N) and the worst-case time is O(N) where N is the number of nodes in the tree.
Like other Trees include AVL trees, Red Black Tree, B tree, 2-3 Tree is also a height balanced tree.
The time complexity of search/insert/delete is O(log N) .
A 2-3 tree is a B-tree of order 3.
Properties of 2-3 tree:
- Nodes with two children are called 2-nodes. The 2-nodes have one data value and two children
- Nodes with three children are called 3-nodes. The 3-nodes have two data values and three children.
- Data is stored in sorted order.
- It is a balanced tree.
- All the leaf nodes are at same level.
- Each node can either be leaf, 2 node, or 3 node.
- Always insertion is done at leaf.
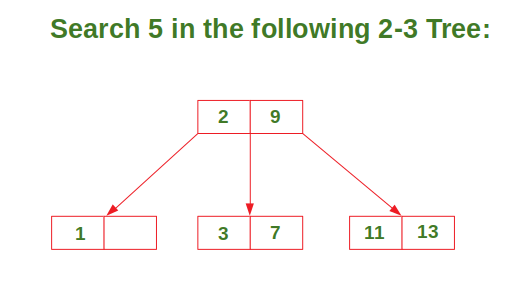
Search: To search a key K in given 2-3 tree T, we follow the following procedure:
Base cases:
- If T is empty, return False (key cannot be found in the tree).
- If current node contains data value which is equal to K, return True.
- If we reach the leaf-node and it doesn’t contain the required key value K, return False.
Recursive Calls:
- If K < currentNode.leftVal, we explore the left subtree of the current node.
- Else if currentNode.leftVal < K < currentNode.rightVal, we explore the middle subtree of the current node.
- Else if K > currentNode.rightVal, we explore the right subtree of the current node.
Consider the following example:



Insertion: There are 3 possible cases in insertion which have been discussed below:
- Case 1: Insert in a node with only one data element
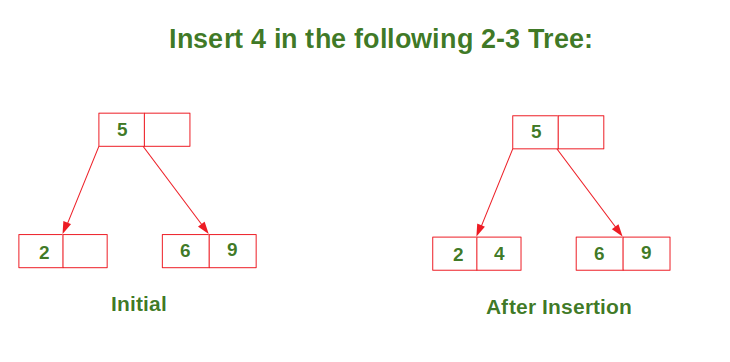
- Case 2: Insert in a node with two data elements whose parent contains only one data element.
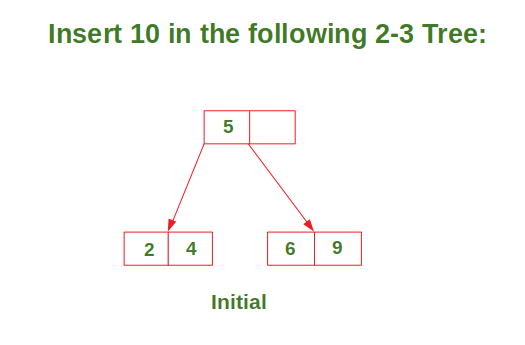
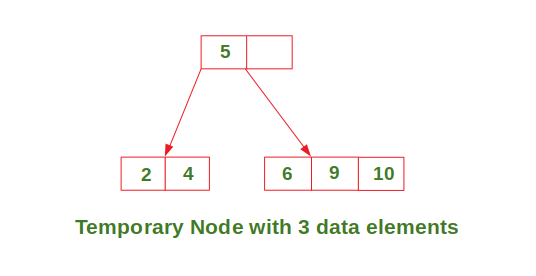
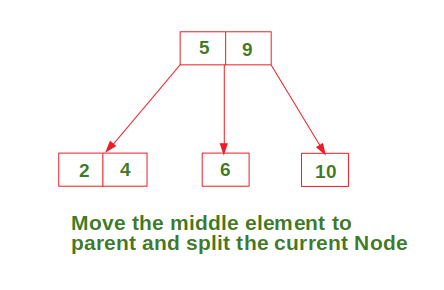
- Case 3: Insert in a node with two data elements whose parent also contains two data elements.
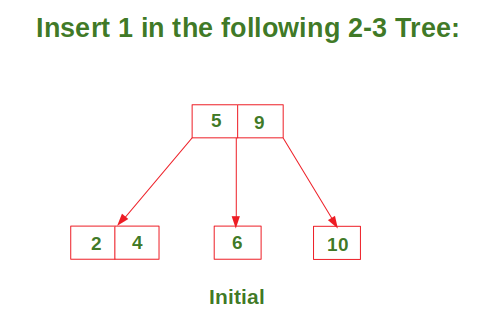
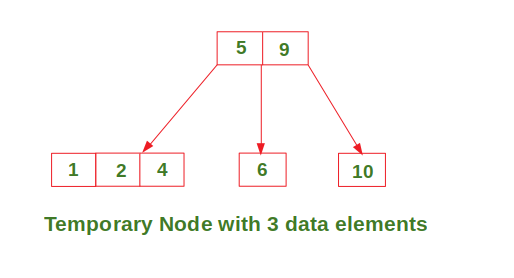
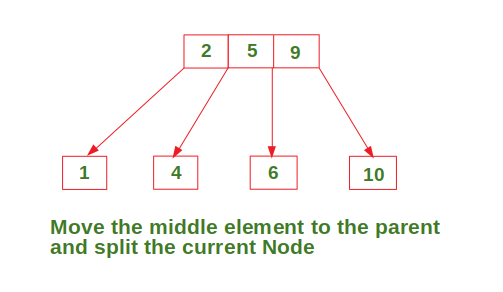
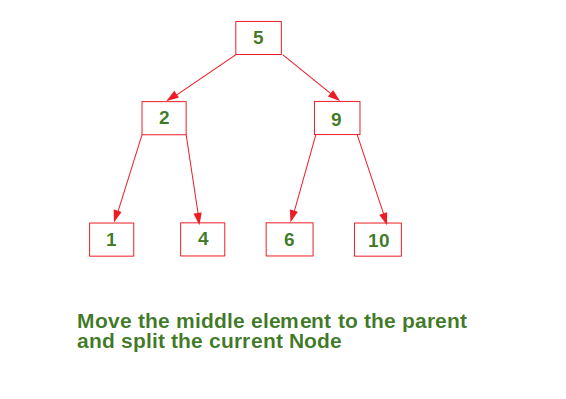
In Deletion Process for a specific value:
- To delete a value, it is replaced by its in-order successor and then removed.
- If a node is left with less than one data value then two nodes must be merged together.
- If a node becomes empty after deleting a value, it is then merged with another node.
To Understand the deletion process-
Consider the 2-3 tree given below

Given 2-3 Tree
delete the following values from it: 69,72, 99, 81.
To delete 69, swap it with its in-order successor, that is, 72. 69 now comes in the leaf node. Remove the value 69 from the leaf node.

After deletion 69
To delete 72, 72 is an internal node. To delete this value swap 72 with its in-order successor 81 so that 72 now becomes a leaf node. Remove the value 72 from the leaf node.

After deletion 72
Now there is a leaf node that has less than 1 data value thereby violating the property of a 2-3 tree. So the node must be merged.
To merge the node, pull down the lowest data value in the parent’s node and merge it with its left sibling.

Rebalancing to Satisfy 23 Tree property
To delete 99, 99 is present in a leaf node, so the data value can be easily removed.

After deletion 99
Now there is a leaf node that has less than 1 data value, thereby violating the property of a 2-3 tree.
So the node must be merged. To merge the node, pull down the lowest data value in the parent’s node and merge it with its left sibling.

Rebalancing to Satisfy 2-3 Tree Property
To delete 81, 81 is an internal node. To delete this value swap 81 with its in-order successor 90 so that 81 now becomes a leaf node. Remove the value 81 from the leaf node.

After deletion 81
Now there is a leaf node that has less than 1 data value, thereby violating the property of a 2-3 tree. So the node must be merged. To merge the node, pull down the lowest data value in the parent’s node and merge it with its left sibling.

Rebalancing to Satisfy 2-3 Tree property
As internal node cannot be empty. So now pull down the lowest data value from the parent’s node and merge the empty node with its left sibling

Rebalancing to Satisfy 2-3 Tree Property
NOTE: In a 2-3 tree, each interior node has either two or three children. This means that a 2-3 tree is not a binary tree.
Share your thoughts in the comments
Please Login to comment...