Permutations of given String

Given a string S, the task is to write a program to print all permutations of a given string. 

A permutation also called an “arrangement number” or “order,” is a rearrangement of the elements of an ordered list S into a one-to-one correspondence with S itself. A string of length N has N! permutations. 

Examples:

Input: S = “ABC”
Output: “ABC”, “ACB”, “BAC”, “BCA”, “CBA”, “CAB”

Input: S = “XY”
Output: “XY”, “YX”

Print permutations of a given string using backtracking:

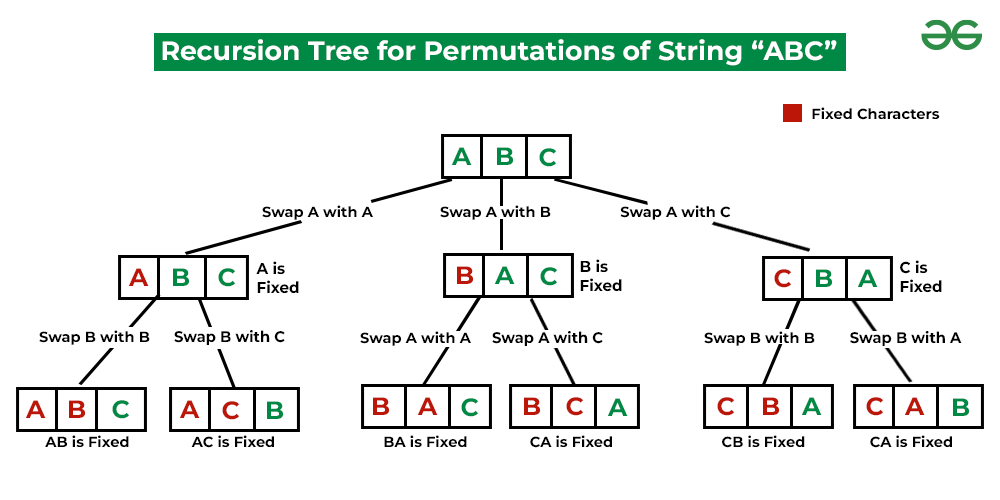
Recursion Tree for permutations of string “ABC”

Follow the given steps to solve the problem:

• Create a function permute() with parameters as input string, starting index of the string, ending index of the string
• Call this function with values input string, 0, size of string – 1
  • In this function, if the value of  L and R is the same then print the same string
    • Else run a for loop from L to R and swap the current element in the for loop with the inputString[L]
    • Then again call this same function by increasing the value of L by 1
    • After that again swap the previously swapped values to initiate backtracking

Below is the implementation of the above approach:

C++14

// C++ program to print all
// permutations with duplicates allowed
#include <bits/stdc++.h>
using namespace std;

// Function to print permutations of string
// This function takes three parameters:
// 1. String
// 2. Starting index of the string
// 3. Ending index of the string.
void permute(string& a, int l, int r)
{
    // Base case
    if (l == r)
        cout << a << endl;
    else {
        // Permutations made
        for (int i = l; i <= r; i++) {

            // Swapping done
            swap(a[l], a[i]);

            // Recursion called
            permute(a, l + 1, r);

            // backtrack
            swap(a[l], a[i]);
        }
    }
}

// Driver Code
int main()
{
    string str = "ABC";
    int n = str.size();

    // Function call
    permute(str, 0, n - 1);
    return 0;
}

// This is code is contributed by rathbhupendra

C

// C program to print all permutations with duplicates
// allowed
#include <stdio.h>
#include <string.h>

/* Function to swap values at two pointers */
void swap(char* x, char* y)
{
    char temp;
    temp = *x;
    *x = *y;
    *y = temp;
}

/* Function to print permutations of string
This function takes three parameters:
1. String
2. Starting index of the string
3. Ending index of the string. */
void permute(char* a, int l, int r)
{
    int i;
    if (l == r)
        printf("%s\n", a);
    else {
        for (i = l; i <= r; i++) {
            swap((a + l), (a + i));
            permute(a, l + 1, r);
            swap((a + l), (a + i)); // backtrack
        }
    }
}

/* Driver code */
int main()
{
    char str[] = "ABC";
    int n = strlen(str);
    permute(str, 0, n - 1);
    return 0;
}

Java

// Java program to print all permutations of a
// given string.
public class Permutation {

    // Function call
    public static void main(String[] args)
    {
        String str = "ABC";
        int n = str.length();
        Permutation permutation = new Permutation();
        permutation.permute(str, 0, n - 1);
    }

    /**
     * permutation function
     * @param str string to calculate permutation for
     * @param l starting index
     * @param r end index
     */
    private void permute(String str, int l, int r)
    {
        if (l == r)
            System.out.println(str);
        else {
            for (int i = l; i <= r; i++) {
                str = swap(str, l, i);
                permute(str, l + 1, r);
                str = swap(str, l, i);
            }
        }
    }

    /**
     * Swap Characters at position
     * @param a string value
     * @param i position 1
     * @param j position 2
     * @return swapped string
     */
    public String swap(String a, int i, int j)
    {
        char temp;
        char[] charArray = a.toCharArray();
        temp = charArray[i];
        charArray[i] = charArray[j];
        charArray[j] = temp;
        return String.valueOf(charArray);
    }
}

// This code is contributed by Mihir Joshi

Python3

# Python3 program to print all permutations with
# duplicates allowed


def toString(List):
    return ''.join(List)

# Function to print permutations of string
# This function takes three parameters:
# 1. String
# 2. Starting index of the string
# 3. Ending index of the string.


def permute(a, l, r):
    if l == r:
        print(toString(a))
    else:
        for i in range(l, r):
            a[l], a[i] = a[i], a[l]
            permute(a, l+1, r)
            a[l], a[i] = a[i], a[l]  # backtrack


# Driver code
string = "ABC"
n = len(string)
a = list(string)

# Function call
permute(a, 0, n)

# This code is contributed by Bhavya Jain

C#

// C# program to print all
// permutations of a given string.
using System;

class GFG {
    /**
    * permutation function
    * @param str string to
    calculate permutation for
    * @param l starting index
    * @param r end index
    */
    private static void permute(String str, int l, int r)
    {
        if (l == r)
            Console.WriteLine(str);
        else {
            for (int i = l; i <= r; i++) {
                str = swap(str, l, i);
                permute(str, l + 1, r);
                str = swap(str, l, i);
            }
        }
    }

    /**
     * Swap Characters at position
     * @param a string value
     * @param i position 1
     * @param j position 2
     * @return swapped string
     */
    public static String swap(String a, int i, int j)
    {
        char temp;
        char[] charArray = a.ToCharArray();
        temp = charArray[i];
        charArray[i] = charArray[j];
        charArray[j] = temp;
        string s = new string(charArray);
        return s;
    }

    // Driver Code
    public static void Main()
    {
        String str = "ABC";
        int n = str.Length;
        permute(str, 0, n - 1);
    }
}

// This code is contributed by mits

Javascript

<script>
// Javascript program to print all permutations of a
// given string.

function permute(str, l, r)
{
    if (l == r)
            document.write(str+"<br>");
        else
        {
            for (let i = l; i <= r; i++)
            {
                str = swap(str, l, i);
                permute(str, l + 1, r);
                str = swap(str, l, i);
            }
        }
}

function swap(a, i, j)
{
    let temp;
let charArray = a.split("");
temp = charArray[i] ;
charArray[i] = charArray[j];
charArray[j] = temp;
return (charArray).join("");
}

let str = "ABC";
let n = str.length;
permute(str, 0, n-1);

// This code is contributed by avanitrachhadiya2155
</script>

PHP

<?php
// PHP program to print all
// permutations of a given string.


/**
* permutation function
* @param str string to
* calculate permutation for
* @param l starting index
* @param r end index
*/
function permute($str, $l, $r)
{
    if ($l == $r)
        echo $str. "\n";
    else
    {
        for ($i = $l; $i <= $r; $i++)
        {
            $str = swap($str, $l, $i);
            permute($str, $l + 1, $r);
            $str = swap($str, $l, $i);
        }
    }
}

/**
* Swap Characters at position
* @param a string value
* @param i position 1
* @param j position 2
* @return swapped string
*/
function swap($a, $i, $j)
{
    $temp;
    $charArray = str_split($a);
    $temp = $charArray[$i] ;
    $charArray[$i] = $charArray[$j];
    $charArray[$j] = $temp;
    return implode($charArray);
}

// Driver Code
$str = "ABC";
$n = strlen($str);
permute($str, 0, $n - 1);

// This code is contributed by mits.
?>

Output

ABC
ACB
BAC
BCA
CBA
CAB

Time Complexity: O(N * N!) Note that there are N! permutations and it requires O(N) time to print a permutation.
Auxiliary Space: O(R – L)

Note: The above solution prints duplicate permutations if there are repeating characters in the input string. Please see the below link for a solution that prints only distinct permutations even if there are duplicates in input.

• Print all distinct permutations of a given string with duplicates.
• Permutations of a given string using STL