Permutations of a given string using STL

A permutation, also called an “arrangement number” or “order”, is a rearrangement of the elements of an ordered list S into a one-to-one correspondence with S itself. A string of length n has n! permutation. 
Source: Mathword

Below are the permutations of string ABC. 

“ABC”, “ACB”, “BAC”, “BCA”, “CBA”, “CAB” 

We have discussed C implementation to print all permutations of a given string using backtracking here. In this post, C++ implementation using STL is discussed.

Method 1 (Using rotate())
std::rotate function rotates elements of a vector/string such that the passed middle element becomes first. For example, if we call rotate for “ABCD” with middle as second element, the string becomes “BCDA” and if we again call rotate with middle as second element, the string becomes “CDAB”. Refer this for a sample program.

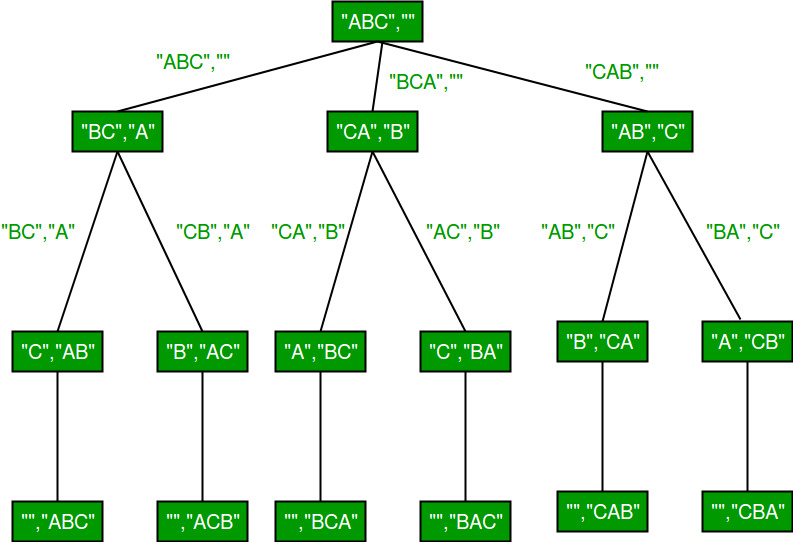
Below is C++ implementation. 

C++

// C++ program to print all permutations with
// duplicates allowed using rotate() in STL
#include <bits/stdc++.h>
using namespace std;

// Function to print permutations of string str,
// out is used to store permutations one by one
void permute(string str, string out)
{
    // When size of str becomes 0, out has a
    // permutation (length of out is n)
    if (str.size() == 0)
    {
        cout << out << endl;
        return;
    }

    // One be one move all characters at
    // the beginning of out (or result)
    for (int i = 0; i < str.size(); i++)
    {
        // Remove first character from str and
        // add it to out
        permute(str.substr(1), out + str[0]);

        // Rotate string in a way second character
        // moves to the beginning.
        rotate(str.begin(), str.begin() + 1, str.end());
    }
}

// Driver code
int main()
{
    string str = "ABC";
    permute(str, "");
    return 0;
}

Output

ABC
ACB
BCA
BAC
CAB
CBA

Time Complexity: O(n*n!) 
Auxiliary Space: O(n) 

Method 2 (using next_permutation)
We can use next_permutation that modifies a string so that it stores lexicographically next permutation. If current string is lexicographically largest, i.e., “CBA”, then next_permutation returns false.

We first sort the string, so that it is converted to lexicographically smallest permutation. Then we one by one call next_permutation until it returns false.

C++

// C++ program to print all permutations with
// duplicates allowed using next_permutation
#include <bits/stdc++.h>
using namespace std;

// Function to print permutations of string str
// using next_permutation
void permute(string str)
{
    // Sort the string in lexicographically
    // ascending order
    sort(str.begin(), str.end());

    // Keep printing next permutation while there
    // is next permutation
    do {
       cout << str << endl;
    } while (next_permutation(str.begin(), str.end()));
}

// Driver code
int main()
{
    string str = "CBA";
    permute(str);
    return 0;
}

Output

ABC
ACB
BAC
BCA
CAB
CBA

Time Complexity: O(n*n!) 
Auxiliary Space: O(1) 

Note that the second method always prints permutations in lexicographically sorted order irrespective of input string.
This article is contributed by Aarti_Rathi and Aditya Goel. If you like GeeksforGeeks and would like to contribute, you can also write an article and mail your article to review-team@geeksforgeeks.org. See your article appearing on the GeeksforGeeks main page and help other Geeks.
Please write comments if you find anything incorrect, or you want to share more information about the topic discussed above