Univariate Linear Regression in Python
Last Updated :
25 Apr, 2023
In this article, we will explain univariate linear regression. It is one of the simplest types of regression. In this regression, we predict our target value on only one independent variable.
Univariate Linear Regression in Python
Univariate Linear Regression is a type of regression in which the target variable depends on only one independent variable. For univariate regression, we use univariate data. For instance, a dataset of points on a line can be considered as univariate data where abscissa can be considered as an input feature and ordinate can be considered as output/target.
Example Of Univariate Linear Regression
For line Y = 2X + 3; the Input feature will be X and Y will be the target.
Concept: For univariate linear regression, there is only one input feature vector. The line of regression will be in the form of the following:
Y = b0 + b1 * X Where, b0 and b1 are the coefficients of regression.
here we try to find the best b0 and b1 by training a model so that our predicted variable y has minimum difference with actual y.
A univariate linear regression model constitutes of several utility functions. We will define each function one by one and at the end, we will combine them in a class to form a working univariate linear regression model object.
Utility Functions in Univariate Linear Regression Model
- Prediction with linear regression
- Cost function
- Gradient Descent For Parameter Estimation
- Update Coefficients
- Stop Iterations
Prediction with linear regression
In this function, we predict the value of y on a given value of x by multiplying and adding the coefficient of regression to the x.
Python3
def predict(x, b0, b1):
return b0 + b1 * x
|
Cost function For Univariate Linear Regression
The cost function computes the error with the current value of regression coefficients. It quantitatively defines how far the model predicted value is from the actual value wrt regression coefficients which have the lowest rate of error.
Mean-Squared Error(MSE) = sum of squares of difference between predicted and actual value
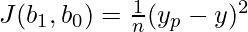
We use square so that positive and negative error does not cancel out each other.
Here:
- y is listed of expected values
- x is the independent variable
- b0 and b1 are regression coefficient
Python3
def cost(x, y, b0, b1):
errors = []
for x, y in zip(x, y):
prediction = predict(x, b0, b1)
expected = y
difference = prediction-expected
errors.append(difference)
mse = sum([error * error for error in errors])/len(errors)
return mse
|
Gradient Descent For Parameter Estimation
We will use gradient descent for updating our regression coefficient. It is an optimization algorithm that we use to train our model. In gradient descent, we take the partial derivative of the cost function wrt to our regression coefficient and multiply with the learning rate alpha and subtract it from our coefficient to adjust our regression coefficient.
For the case of simplicity we will apply gradient descent on only one row element and
try to estimate our univaraite linear regression coeficient on the basis of
this gradient descent.
![Rendered by QuickLaTeX.com \begin {aligned} {J}'b_1 &=\frac{\partial J(b_1,b_0)}{\partial b_1} \\ &= \frac{\partial}{\partial b_1} \left[\frac{1}{n} (y_p-y)^2 \right] \\ &= \frac{2(y_p-y)}{n}\frac{\partial}{\partial b_1}\left [(y_p-y) \right ] \\ &= \frac{2(y_p-y)}{n}\frac{\partial}{\partial b_1}\left [((xb_1+b_0)-y) \right ] \\ &= \frac{2(y_p-y)}{n}\left[\frac{\partial(xb_1+b_0)}{\partial b_1}-\frac{\partial(y)}{\partial b_1}\right] \\ &= \frac{2(y_p-y)}{n}\left [ x - 0 \right ] \\ &= \frac{1}{n}(y_p-y)[2x] \end {aligned}](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-af60b75f0f9653fafb9b99b5aa49eac3_l3.png)
![Rendered by QuickLaTeX.com \begin {aligned} {J}'b_0 &=\frac{\partial J(b_1,b_0)}{\partial b_0} \\ &= \frac{\partial}{\partial b_0} \left[\frac{1}{n} (y_p-y)^2 \right] \\ &= \frac{2(y_p-y)}{n}\frac{\partial}{\partial b_0}\left [(y_p-y) \right ] \\ &= \frac{2(y_p-y)}{n}\frac{\partial}{\partial b}\left [((xW^T+b)-y) \right ] \\ &= \frac{2(y_p-y)}{n}\left[\frac{\partial(xb_1+b_0)}{\partial b_0}-\frac{\partial(y)}{\partial b_0}\right] \\ &= \frac{2(y_p-y)}{n}\left [ 1 - 0 \right ] \\ &= \frac{1}{n}(y_p-y)[2] \end {aligned}](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-e1316caa947d9757a0d8bff1a7ab6533_l3.png)
Since our cost function has two parameters b_1 and b_0 we have taken the derivative of the cost function wrt b_1 and then wrt b_0.
Python function for Gradient Descent.
Python3
def grad_fun(x, y, b0, b1, i):
return sum([
2*(predict(xi, b0, b1)-yi)*1
if i == 0
else 2*(predict(xi, b0, b1)-yi)*xi
for xi, yi in zip(x, y)
])/len(x)
|
Update Coefficients Of Univariate Linear Regression.
At each iteration (epoch), the values of the regression coefficient are updated by a specific value wrt to the error from the previous iteration. This updation is very crucial and is the crux of the machine learning applications that you write. Updating the coefficients is done by penalizing their value with a fraction of the error that its previous values caused. This fraction is called the learning rate. This defines how fast our model reaches to point of convergence(the point where the error is ideally 0).
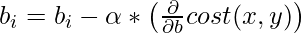
Python3
def update_coeff(x, y, b0, b1, i, alpha):
bi -= alpha * cost_derivative(x, y, b0, b1, i)
return bi
|
Stop Iterations
This is the function that is used to specify when the iterations should stop. As per the user, the algorithm stop_iteration generally returns true in the following conditions:
- Max Iteration: Model is trained for a specified number of iterations.
- Error value: Depending upon the value of the previous error, the algorithm decides whether to continue or stop.
- Accuracy: Depending upon the last accuracy of the model, if it is larger than the mentioned accuracy, the algorithm returns True,
- Hybrid: This is more often used. This combines more than one above mentioned conditions along with an exceptional break option. The exceptional break is a condition where training continues until when something bad happens. Something bad might include an overflow of results, time constraints exceeded, etc.
Having all the utility functions defined let’s see the pseudo-code followed by its implementation:
Pseudocode for linear regression:
x, y is the given data.
(b0, b1) <-- (0, 0)
i = 0
while True:
if stop_iteration(i):
break
else:
b0 = update_coeff(x, y, b0, b1, 0, alpha)
b1 = update_coeff(x, y, b0, b1, 1, alpha)Full Implementation of univariate using Python
Python3
class LinearRegressor:
def __init__(self, x, y, alpha=0.01, b0=0, b1=0):
self.i = 0
self.x = x
self.y = y
self.alpha = alpha
self.b0 = b0
self.b1 = b1
if len(x) != len(y):
raise TypeError()
def predict(model, x):
return model.b0 + model.b1 * x
def grad_fun(model, i):
x, y, b0, b1 = model.x, model.y, model.b0, model.b1
predict = model.predict
return sum([
2 * (predict(xi) - yi) * 1
if i == 0
else (predict(xi) - yi) * xi
for xi, yi in zip(x, y)
]) / len(x)
def update_coeff(model, i):
cost_derivative = model.cost_derivative
if i == 0:
model.b0 -= model.alpha * cost_derivative(i)
elif i == 1:
model.b1 -= model.alpha * cost_derivative(i)
def stop_iteration(model, max_epochs=1000):
model.i += 1
if model.i == max_epochs:
return True
else:
return False
def fit(model):
update_coeff = model.update_coeff
model.i = 0
while True:
if model.stop_iteration():
break
else:
update_coeff(0)
update_coeff(1)
|
Initializing the Model object
Python3
linearRegressor = LinearRegressor(
x=[i for i in range(12)],
y=[2 * i + 3 for i in range(12)],
alpha=0.03
)
linearRegressor.fit()
print(linearRegressor.predict(12))
|
Output:
27.00000004287766
Share your thoughts in the comments
Please Login to comment...