Solving Linear Regression in Python
Last Updated :
16 Jul, 2020
Linear regression is a common method to model the relationship between a dependent variable and one or more independent variables. Linear models are developed using the parameters which are estimated from the data. Linear regression is useful in prediction and forecasting where a predictive model is fit to an observed data set of values to determine the response. Linear regression models are often fitted using the least-squares approach where the goal is to minimize the error.
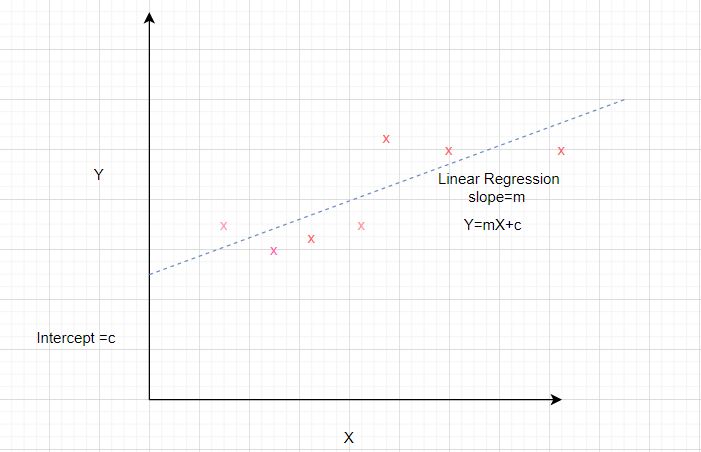
Consider a dataset where the independent attribute is represented by x and the dependent attribute is represented by y.

It is known that the equation of a straight line is y = mx + b where m is the slope and b is the intercept.
In order to prepare a simple regression model of the given dataset, we need to calculate the slope and intercept of the line which best fits the data points.
How to calculate slope and intercept?
Mathematical formula to calculate slope and intercept are given below
Slope = Sxy/Sxx
where Sxy and Sxx are sample covariance and sample variance respectively.
Intercept = ymean – slope* xmean
Let us use these relations to determine the linear regression for the above dataset. For this we calculate the xmean, ymean, Sxy, Sxx as shown in the table.
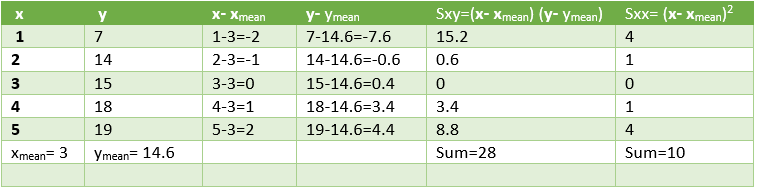
As per the above formulae,
Slope = 28/10 = 2.8
Intercept = 14.6 – 2.8 * 3 = 6.2
Therefore,
The desired equation of the regression model is y = 2.8 x + 6.2
We shall use these values to predict the values of y for the given values of x. The performance of the model can be analyzed by calculating the root mean square error and R2 value.
Calculations are shown below.
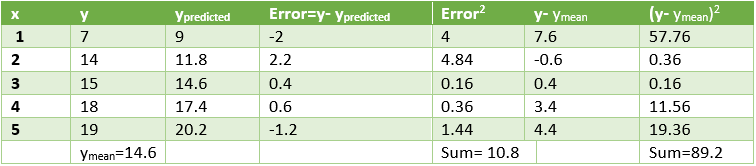
Squared Error=10.8 which means that mean squared error =3.28
Coefficient of Determination (R2) = 1- 10.8 / 89.2 = 0.878
Low value of error and high value of R2 signify that the
linear regression fits data well
Let us see the Python Implementation of linear regression for this dataset.
Code 1: Import all the necessary Libraries.
import numpy as np
import matplotlib.pyplot as plt
from sklearn.linear_model import LinearRegression
from sklearn.metrics import mean_squared_error, r2_score
import statsmodels.api as sm
|
Code 2: Generate the data. Calculate xmean, ymean, Sxx, Sxy to find the value of slope and intercept of regression line.
x = np.array([1,2,3,4,5])
y = np.array([7,14,15,18,19])
n = np.size(x)
x_mean = np.mean(x)
y_mean = np.mean(y)
x_mean,y_mean
Sxy = np.sum(x*y)- n*x_mean*y_mean
Sxx = np.sum(x*x)-n*x_mean*x_mean
b1 = Sxy/Sxx
b0 = y_mean-b1*x_mean
print('slope b1 is', b1)
print('intercept b0 is', b0)
plt.scatter(x,y)
plt.xlabel('Independent variable X')
plt.ylabel('Dependent variable y')
|
Output:
slope b1 is 2.8
intercept b0 is 6.200000000000001
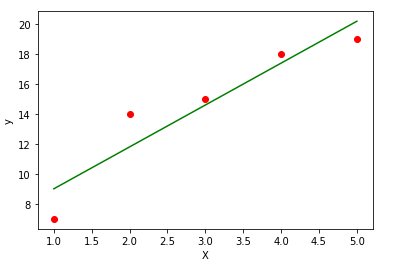
Code 3: Plot the given data points and fit the regression line.
y_pred = b1 * x + b0
plt.scatter(x, y, color = 'red')
plt.plot(x, y_pred, color = 'green')
plt.xlabel('X')
plt.ylabel('y')
|
Code 4: Analyze the performance of the model by calculating mean squared error and R2
error = y - y_pred
se = np.sum(error**2)
print('squared error is', se)
mse = se/n
print('mean squared error is', mse)
rmse = np.sqrt(mse)
print('root mean square error is', rmse)
SSt = np.sum((y - y_mean)**2)
R2 = 1- (se/SSt)
print('R square is', R2)
|
Output:
squared error is 10.800000000000004
mean squared error is 2.160000000000001
root mean square error is 1.4696938456699071
R square is 0.8789237668161435
Code 5: Use scikit library to confirm the above steps.
x = x.reshape(-1,1)
regression_model = LinearRegression()
regression_model.fit(x, y)
y_predicted = regression_model.predict(x)
mse=mean_squared_error(y,y_predicted)
rmse = np.sqrt(mean_squared_error(y, y_predicted))
r2 = r2_score(y, y_predicted)
print('Slope:' ,regression_model.coef_)
print('Intercept:', regression_model.intercept_)
print('MSE:',mse)
print('Root mean squared error: ', rmse)
print('R2 score: ', r2)
|
Output:
Slope: [2.8]
Intercept: 6.199999999999999
MSE: 2.160000000000001
Root mean squared error: 1.4696938456699071
R2 score: 0.8789237668161435
Conclusion: This article helps to understand the mathematics behind simple regression and implement the same using Python.
Like Article
Suggest improvement
Share your thoughts in the comments
Please Login to comment...