Introduction to Binary Search Tree – Data Structure and Algorithm Tutorials
Last Updated :
19 Apr, 2024
Binary Search Tree is a data structure used in computer science for organizing and storing data in a sorted manner. Binary search tree follows all properties of binary tree and its left child contains values less than the parent node and the right child contains values greater than the parent node. This hierarchical structure allows for efficient Searching, Insertion, and Deletion operations on the data stored in the tree.
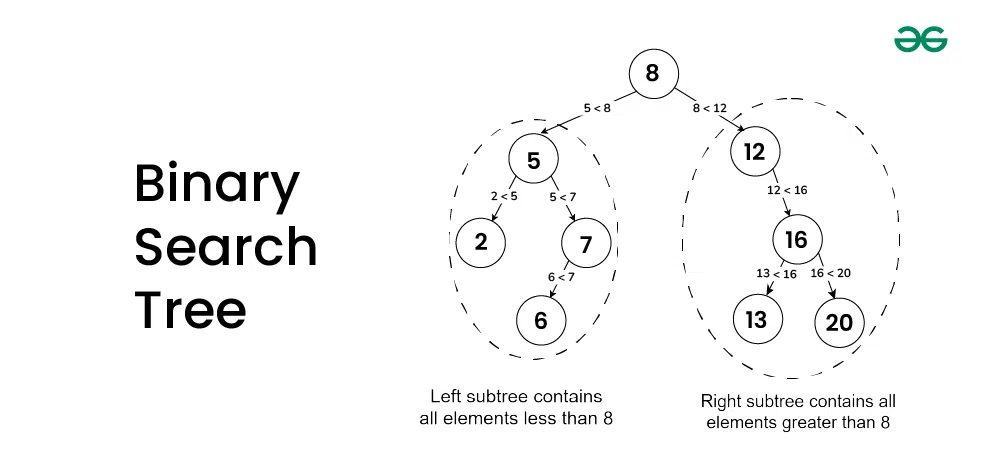
Binary Search Tree
What is Binary Search Tree?
Binary Search Tree (BST) is a special type of binary tree in which the left child of a node has a value less than the node’s value and the right child has a value greater than the node’s value. This property is called the BST property and it makes it possible to efficiently search, insert, and delete elements in the tree.
Properties of Binary Search Tree:
- The left subtree of a node contains only nodes with keys lesser than the node’s key.
- The right subtree of a node contains only nodes with keys greater than the node’s key.
- This means everything to the left of the root is less than the value of the root and everything to the right of the root is greater than the value of the root. Due to this performing, a binary search is very easy.
- The left and right subtree each must also be a binary search tree.
- There must be no duplicate nodes(BST may have duplicate values with different handling approaches)
Handling duplicate values in the Binary Search Tree:
- We must follow a consistent process throughout i.e. either store duplicate value at the left or store the duplicate value at the right of the root, but be consistent with your approach.
1. Searching a node in BST:
Searching in BST means to locate a specific node in the data structure. In Binary search tree, searching a node is easy because of its a specific order. The steps of searching a node in Binary Search tree are listed as follows –
- First, compare the element to be searched with the root element of the tree.
- If root is matched with the target element, then return the node’s location.
- If it is not matched, then check whether the item is less than the root element, if it is smaller than the root element, then move to the left subtree.
- If it is larger than the root element, then move to the right subtree.
- Repeat the above procedure recursively until the match is found.
- If the element is not found or not present in the tree, then return NULL.
Now, let’s understand the searching in binary tree using an example:
Below is given a BST and we have to search for element 6.
Code:
Below is the implementation of searching in BST:
C++
// C++ function to search a given key in a given BST
#include <iostream>
using namespace std;
struct node {
int key;
struct node *left, *right;
};
// A utility function to create a new BST node
struct node* newNode(int item)
{
struct node* temp
= new struct node;
temp->key = item;
temp->left = temp->right = NULL;
return temp;
}
// A utility function to insert
// a new node with given key in BST
struct node* insert(struct node* node, int key)
{
// If the tree is empty, return a new node
if (node == NULL)
return newNode(key);
// Otherwise, recur down the tree
if (key < node->key)
node->left = insert(node->left, key);
else if (key > node->key)
node->right = insert(node->right, key);
// Return the (unchanged) node pointer
return node;
}
// Utility function to search a key in a BST
struct node* search(struct node* root, int key)
{
// Base Cases: root is null or key is present at root
if (root == NULL || root->key == key)
return root;
// Key is greater than root's key
if (root->key < key)
return search(root->right, key);
// Key is smaller than root's key
return search(root->left, key);
}
// C function to search a given key in a given BST
#include <stdio.h>
#include <stdlib.h>
struct node {
int key;
struct node *left, *right;
};
// A utility function to create a new BST node
struct node* newNode(int item)
{
struct node* temp
= (struct node*)malloc(sizeof(struct node));
temp->key = item;
temp->left = temp->right = NULL;
return temp;
}
// A utility function to insert
// a new node with given key in BST
struct node* insert(struct node* node, int key)
{
// If the tree is empty, return a new node
if (node == NULL)
return newNode(key);
// Otherwise, recur down the tree
if (key < node->key)
node->left = insert(node->left, key);
else if (key > node->key)
node->right = insert(node->right, key);
// Return the (unchanged) node pointer
return node;
}
// Utility function to search a key in a BST
struct node* search(struct node* root, int key)
{
// Base Cases: root is null or key is present at root
if (root == NULL || root->key == key)
return root;
// Key is greater than root's key
if (root->key < key)
return search(root->right, key);
// Key is smaller than root's key
return search(root->left, key);
}
// Java program to search a given key in a given BST
class Node {
int key;
Node left, right;
public Node(int item) {
key = item;
left = right = null;
}
}
class BinarySearchTree {
Node root;
// Constructor
BinarySearchTree() {
root = null;
}
// A utility function to insert
// a new node with given key in BST
Node insert(Node node, int key) {
// If the tree is empty, return a new node
if (node == null) {
node = new Node(key);
return node;
}
// Otherwise, recur down the tree
if (key < node.key)
node.left = insert(node.left, key);
else if (key > node.key)
node.right = insert(node.right, key);
// Return the (unchanged) node pointer
return node;
}
// Utility function to search a key in a BST
Node search(Node root, int key) {
// Base Cases: root is null or key is present at root
if (root == null || root.key == key)
return root;
// Key is greater than root's key
if (root.key < key)
return search(root.right, key);
// Key is smaller than root's key
return search(root.left, key);
}
# Python3 function to search a given key in a given BST
class Node:
# Constructor to create a new node
def __init__(self, key):
self.key = key
self.left = None
self.right = None
# A utility function to insert
# a new node with the given key in BST
def insert(node, key):
# If the tree is empty, return a new node
if node is None:
return Node(key)
# Otherwise, recur down the tree
if key < node.key:
node.left = insert(node.left, key)
elif key > node.key:
node.right = insert(node.right, key)
# Return the (unchanged) node pointer
return node
# Utility function to search a key in a BST
def search(root, key):
# Base Cases: root is null or key is present at root
if root is None or root.key == key:
return root
# Key is greater than root's key
if root.key < key:
return search(root.right, key)
# Key is smaller than root's key
return search(root.left, key)
// Javascript function to search a given key in a given BST
class Node {
constructor(key) {
this.key = key;
this.left = null;
this.right = null;
}
}
// A utility function to insert
// a new node with given key in BST
function insert(node, key) {
// If the tree is empty, return a new node
if (node === null) {
return new Node(key);
}
// Otherwise, recur down the tree
if (key < node.key) {
node.left = insert(node.left, key);
} else if (key > node.key) {
node.right = insert(node.right, key);
}
// Return the (unchanged) node pointer
return node;
}
// Utility function to search a key in a BST
function search(root, key) {
// Base Cases: root is null or key is present at root
if (root === null || root.key === key) {
return root;
}
// Key is greater than root's key
if (root.key < key) {
return search(root.right, key);
}
// Key is smaller than root's key
return search(root.left, key);
}
A new key is always inserted at the leaf. Start searching a key from the root till a leaf node. Once a leaf node is found, the new node is added as a child of the leaf node.
Code:
Below is the implementation of the Insertion of a single node in Binary Search Tree:
C++
// Given Node Structure
struct node
{
int key;
struct node *left, *right;
};
// Function to create a new BST node
struct node* newNode(int item)
{
struct node* temp = (struct node*)malloc(
sizeof(struct node));
temp->key = item;
temp->left = temp->right = NULL;
return temp;
}
// Function to insert a new node with
// given key in BST
struct node* insert(struct node* node, int key)
{
// If the tree is empty, return a new node
if (node == NULL)
return newNode(key);
// Otherwise, recur down the tree
if (key < node->key)
{
node->left = insert(node->left, key);
}
else if (key > node->key)
{
node->right = insert(node->right, key);
}
// Return the node pointer
return node;
}
// Given Node Structure
struct node {
int key;
struct node *left, *right;
};
// Function to create a new BST node
struct node* newNode(int item)
{
struct node* temp
= (struct node*)malloc(
sizeof(struct node));
temp->key = item;
temp->left = temp->right = NULL;
return temp;
}
// Function to insert a new node with
// given key in BST
struct node* insert(struct node* node, int key)
{
// If the tree is empty, return a new node
if (node == NULL)
return newNode(key);
// Otherwise, recur down the tree
if (key < node->key) {
node->left = insert(node->left, key);
}
else if (key > node->key) {
node->right = insert(node->right, key);
}
// Return the node pointer
return node;
}
class GFG {
// Given Node Structure
static class node {
int key;
node left, right;
};
// Function to create a new BST node
static node newNode(int item)
{
node temp = new node();
temp.key = item;
temp.left = temp.right = null;
return temp;
}
// Function to insert a new node with
// given key in BST
static node insert(node node, int key)
{
// If the tree is empty, return a new node
if (node == null)
return newNode(key);
// Otherwise, recur down the tree
if (key < node.key) {
node.left = insert(node.left, key);
}
else if (key > node.key) {
node.right = insert(node.right, key);
}
// Return the node
return node;
}
}
# Given Node Structure
class Node:
def __init__(self, key):
self.key = key
self.left = None
self.right = None
# Function to insert a new node with
# given key in BST
def insert(node, key):
# If the tree is empty, return a new node
if node is None:
return Node(key)
# Otherwise, recur down the tree
if key < node.key:
node.left = insert(node.left, key)
elif key > node.key:
node.right = insert(node.right, key)
# Return the node pointer
return node
// Given Node Structure
class Node
{
constructor(key){
this.key = key;
this.left = null;
this.right = null;
}
}
// Function to insert a new node with
// given key in BST
function insert(node, key)
{
// If the tree is empty, return a new node
if (node == null)
return new Node(key);
// Otherwise, recur down the tree
if (key < node.key)
{
node.left = insert(node.left, key);
}
else if (key > node.key)
{
node.right = insert(node.right, key);
}
// Return the node pointer
return node;
}
Time Complexity: O(N), where N is the number of nodes of the BST
Auxiliary Space: O(1)
It is used to delete a node with specific key from the BST and return the new BST.
Different scenarios for deleting the node:
Node to be deleted is the leaf node :
Its simple you can just null it out.

Node to be deleted has one child :
You can just replace the node with the child node.

Node to be deleted has two child :
Here we have to delete the node is such a way, that the resulting tree follows the properties of a BST. The trick is to find the inorder successor of the node. Copy contents of the inorder successor to the node, and delete the inorder successor.

Take Care of following things while deleting a node of a BST:
- Need to figure out what will be the replacement of the node to be deleted.
- Want minimal disruption to the existing tree structure
- Can take the replacement node from the deleted nodes left or right subtree.
- If taking if from the left subtree, we have to take the largest value in the left subtree.
- If taking if from the right subtree, we have to take the smallest value in the right subtree.
Code:
Below is the implementation of the deletion in BST:
C++
// C++ program to delete
// a node of BST
// Given Node node
struct node {
int key;
struct node *left, *right;
};
// Function to create a new BST node
struct node* newNode(int item)
{
struct node* temp
= (struct node*)malloc(
sizeof(struct node));
temp->key = item;
temp->left = temp->right = NULL;
return temp;
}
// Function to insert a new node with
// given key in BST
struct node* insert(struct node* node, int key)
{
// If the tree is empty, return a new node
if (node == NULL)
return newNode(key);
// Otherwise, recur down the tree
if (key < node->key) {
node->left = insert(node->left, key);
}
else if (key > node->key) {
node->right = insert(node->right, key);
}
// Return the node pointer
return node;
}
// Function that returns the node with minimum
// key value found in that tree
struct node* minValueNode(struct node* node)
{
struct node* current = node;
// Loop down to find the leftmost leaf
while (current && current->left != NULL)
current = current->left;
return current;
}
// Function that deletes the key and
// returns the new root
struct node* deleteNode(struct node* root,
int key)
{
// base Case
if (root == NULL)
return root;
// If the key to be deleted is
// smaller than the root's key,
// then it lies in left subtree
if (key < root->key) {
root->left
= deleteNode(root->left, key);
}
// If the key to be deleted is
// greater than the root's key,
// then it lies in right subtree
else if (key > root->key) {
root->right
= deleteNode(root->right, key);
}
// If key is same as root's key,
// then this is the node
// to be deleted
else {
// Node with only one child
// or no child
if (root->left == NULL) {
struct node* temp = root->right;
free(root);
return temp;
}
else if (root->right == NULL) {
struct node* temp = root->left;
free(root);
return temp;
}
// Node with two children:
// Get the inorder successor(smallest
// in the right subtree)
struct node* temp = minValueNode(root->right);
// Copy the inorder successor's
// content to this node
root->key = temp->key;
// Delete the inorder successor
root->right
= deleteNode(root->right, temp->key);
}
return root;
}
// C program to delete
// a node of BST
// Given Node node
struct node {
int key;
struct node *left, *right;
};
// Function to create a new BST node
struct node* newNode(int item)
{
struct node* temp
= (struct node*)malloc(
sizeof(struct node));
temp->key = item;
temp->left = temp->right = NULL;
return temp;
}
// Function to insert a new node with
// given key in BST
struct node* insert(struct node* node, int key)
{
// If the tree is empty, return a new node
if (node == NULL)
return newNode(key);
// Otherwise, recur down the tree
if (key < node->key) {
node->left = insert(node->left, key);
}
else if (key > node->key) {
node->right = insert(node->right, key);
}
// Return the node pointer
return node;
}
// Function that returns the node with minimum
// key value found in that tree
struct node* minValueNode(struct node* node)
{
struct node* current = node;
// Loop down to find the leftmost leaf
while (current && current->left != NULL)
current = current->left;
return current;
}
// Function that deletes the key and
// returns the new root
struct node* deleteNode(struct node* root,
int key)
{
// base Case
if (root == NULL)
return root;
// If the key to be deleted is
// smaller than the root's key,
// then it lies in left subtree
if (key < root->key) {
root->left
= deleteNode(root->left, key);
}
// If the key to be deleted is
// greater than the root's key,
// then it lies in right subtree
else if (key > root->key) {
root->right
= deleteNode(root->right, key);
}
// If key is same as root's key,
// then this is the node
// to be deleted
else {
// Node with only one child
// or no child
if (root->left == NULL) {
struct node* temp = root->right;
free(root);
return temp;
}
else if (root->right == NULL) {
struct node* temp = root->left;
free(root);
return temp;
}
// Node with two children:
// Get the inorder successor(smallest
// in the right subtree)
struct node* temp = minValueNode(root->right);
// Copy the inorder successor's
// content to this node
root->key = temp->key;
// Delete the inorder successor
root->right
= deleteNode(root->right, temp->key);
}
return root;
}
// Java program for Delete a Node of BST
class GFG {
// Given Node node
static class node {
int key;
node left, right;
};
// Function to create a new BST node
static node newNode(int item)
{
node temp = new node();
temp.key = item;
temp.left = temp.right = null;
return temp;
}
// Function to insert a new node with
// given key in BST
static node insert(node node, int key)
{
// If the tree is empty, return a new node
if (node == null)
return newNode(key);
// Otherwise, recur down the tree
if (key < node.key) {
node.left = insert(node.left, key);
}
else if (key > node.key) {
node.right = insert(node.right, key);
}
// Return the node
return node;
}
// Function that returns the node with minimum
// key value found in that tree
static node minValueNode(node node)
{
node current = node;
// Loop down to find the leftmost leaf
while (current != null && current.left != null)
current = current.left;
return current;
}
// Function that deletes the key and
// returns the new root
static node deleteNode(node root, int key)
{
// base Case
if (root == null)
return root;
// If the key to be deleted is
// smaller than the root's key,
// then it lies in left subtree
if (key < root.key) {
root.left = deleteNode(root.left, key);
}
// If the key to be deleted is
// greater than the root's key,
// then it lies in right subtree
else if (key > root.key) {
root.right = deleteNode(root.right, key);
}
// If key is same as root's key,
// then this is the node
// to be deleted
else {
// Node with only one child
// or no child
if (root.left == null) {
node temp = root.right;
return temp;
}
else if (root.right == null) {
node temp = root.left;
return temp;
}
// Node with two children:
// Get the inorder successor(smallest
// in the right subtree)
node temp = minValueNode(root.right);
// Copy the inorder successor's
// content to this node
root.key = temp.key;
// Delete the inorder successor
root.right = deleteNode(root.right, temp.key);
}
return root;
}
# Python program to delete a node of BST
# Given Node node
class Node:
def __init__(self, key):
self.key = key
self.left = None
self.right = None
# Function to insert a new node with
# given key in BST
def insert(root, key):
# If the tree is empty, return a new node
if root is None:
return Node(key)
# Otherwise, recur down the tree
if key < root.key:
root.left = insert(root.left, key)
elif key > root.key:
root.right = insert(root.right, key)
# Return the node pointer
return root
# Function to do inorder traversal of BST
def inorder(root):
if root:
inorder(root.left)
print(root.key, end=" ")
inorder(root.right)
# Function that returns the node with minimum
# key value found in that tree
def minValueNode(node):
current = node
# Loop down to find the leftmost leaf
while current and current.left is not None:
current = current.left
return current
# Function that deletes the key and
# returns the new root
def deleteNode(root, key):
# base Case
if root is None:
return root
# If the key to be deleted is
# smaller than the root's key,
# then it lies in left subtree
if key < root.key:
root.left = deleteNode(root.left, key)
# If the key to be deleted is
# greater than the root's key,
# then it lies in right subtree
elif key > root.key:
root.right = deleteNode(root.right, key)
# If key is same as root's key,
# then this is the node
# to be deleted
else:
# Node with only one child
# or no child
if root.left is None:
temp = root.right
root = None
return temp
elif root.right is None:
temp = root.left
root = None
return temp
# Node with two children:
# Get the inorder successor(smallest
# in the right subtree)
temp = minValueNode(root.right)
# Copy the inorder successor's
# content to this node
root.key = temp.key
# Delete the inorder successor
root.right = deleteNode(root.right, temp.key)
return root
In case of binary search trees (BST), Inorder traversal gives nodes in non-decreasing order. We visit the left child first, then the root, and then the right child.
Below is the implementation of how to do inorder traversal of a Binary Search Tree:
C++
// C++ program to implement
// inorder traversal of BST
#include <bits/stdc++.h>
using namespace std;
// Given Node node
struct node
{
int key;
struct node *left, *right;
};
// Function to create a new BST node
struct node* newNode(int item)
{
struct node* temp = (struct node*)malloc(
sizeof(struct node));
temp->key = item;
temp->left = temp->right = NULL;
return temp;
}
// Function to insert a new node with
// given key in BST
struct node* insert(struct node* node, int key)
{
// If the tree is empty, return a new node
if (node == NULL)
return newNode(key);
// Otherwise, recur down the tree
if (key < node->key)
{
node->left = insert(node->left, key);
}
else if (key > node->key)
{
node->right = insert(node->right, key);
}
// Return the node pointer
return node;
}
// Function to do inorder traversal of BST
void inorder(struct node* root)
{
if (root != NULL)
{
inorder(root->left);
cout << " " << root->key;
inorder(root->right);
}
}
// Driver Code
int main()
{
/* Let us create following BST
50
/ \
30 70
/ \ / \
20 40 60 80
*/
struct node* root = NULL;
// Creating the BST
root = insert(root, 50);
insert(root, 30);
insert(root, 20);
insert(root, 40);
insert(root, 70);
insert(root, 60);
insert(root, 80);
// Function Call
inorder(root);
return 0;
}
// This code is contributed by shivanisinghss2110
// C program to implement
// inorder traversal of BST
#include <stdio.h>
#include <stdlib.h>
// Given Node node
struct node {
int key;
struct node *left, *right;
};
// Function to create a new BST node
struct node* newNode(int item)
{
struct node* temp
= (struct node*)malloc(
sizeof(struct node));
temp->key = item;
temp->left = temp->right = NULL;
return temp;
}
// Function to insert a new node with
// given key in BST
struct node* insert(struct node* node, int key)
{
// If the tree is empty, return a new node
if (node == NULL)
return newNode(key);
// Otherwise, recur down the tree
if (key < node->key) {
node->left = insert(node->left, key);
}
else if (key > node->key) {
node->right = insert(node->right, key);
}
// Return the node pointer
return node;
}
// Function to do inorder traversal of BST
void inorder(struct node* root)
{
if (root != NULL) {
inorder(root->left);
printf("%d ", root->key);
inorder(root->right);
}
}
// Driver Code
int main()
{
/* Let us create following BST
50
/ \
30 70
/ \ / \
20 40 60 80
*/
struct node* root = NULL;
// Creating the BST
root = insert(root, 50);
insert(root, 30);
insert(root, 20);
insert(root, 40);
insert(root, 70);
insert(root, 60);
insert(root, 80);
// Function Call
inorder(root);
return 0;
}
import java.io.*;
// Java program for Inorder Traversal
class GFG {
// Given Node node
static class node {
int key;
node left, right;
};
// Function to create a new BST node
static node newNode(int item)
{
node temp = new node();
temp.key = item;
temp.left = temp.right = null;
return temp;
}
// Function to insert a new node with
// given key in BST
static node insert(node node, int key)
{
// If the tree is empty, return a new node
if (node == null)
return newNode(key);
// Otherwise, recur down the tree
if (key < node.key) {
node.left = insert(node.left, key);
}
else if (key > node.key) {
node.right = insert(node.right, key);
}
// Return the node
return node;
}
// Function to do inorder traversal of BST
static void inorder(node root)
{
if (root != null) {
inorder(root.left);
System.out.print(" " + root.key);
inorder(root.right);
}
}
// Driver Code
public static void main(String[] args)
{
/* Let us create following BST
50
/ \
30 70
/ \ / \
20 40 60 80
*/
node root = null;
// inserting value 50
root = insert(root, 50);
// inserting value 30
insert(root, 30);
// inserting value 20
insert(root, 20);
// inserting value 40
insert(root, 40);
// inserting value 70
insert(root, 70);
// inserting value 60
insert(root, 60);
// inserting value 80
insert(root, 80);
// print the BST
inorder(root);
}
}
// This code is contributed by abhijitjadhav1998
# Python program to implement
# inorder traversal of BST
# Given Node node
class Node:
def __init__(self, key):
self.key = key
self.left = None
self.right = None
# Function to create a new BST node
def newNode(item):
temp = Node(item)
temp.key = item
temp.left = temp.right = None
return temp
# Function to insert a new node with
# given key in BST
def insert(node, key):
# If the tree is empty, return a new node
if node is None:
return newNode(key)
# Otherwise, recur down the tree
if key < node.key:
node.left = insert(node.left, key)
elif key > node.key:
node.right = insert(node.right, key)
# Return the node pointer
return node
# Function to do inorder traversal of BST
def inorder(root):
if root:
inorder(root.left)
print(root.key, end=" ")
inorder(root.right)
# Driver Code
if __name__ == '__main__':
# Let us create following BST
# 50
# / \
# 30 70
# / \ / \
# 20 40 60 80
root = None
# Creating the BST
root = insert(root, 50)
insert(root, 30)
insert(root, 20)
insert(root, 40)
insert(root, 70)
insert(root, 60)
insert(root, 80)
# Function Call
inorder(root)
#This code is contributed by japmeet01
Output 20 30 40 50 60 70 80
Time Complexity: O(N), where N is the number of nodes of the BST
Auxiliary Space: O(1)
Applications of BST:
- Graph algorithms: BSTs can be used to implement graph algorithms, such as in minimum spanning tree algorithms.
- Priority Queues: BSTs can be used to implement priority queues, where the element with the highest priority is at the root of the tree, and elements with lower priority are stored in the subtrees.
- Self-balancing binary search tree: BSTs can be used as a self-balancing data structures such as AVL tree and Red-black tree.
- Data storage and retrieval: BSTs can be used to store and retrieve data quickly, such as in databases, where searching for a specific record can be done in logarithmic time.
Advantages:
- Fast search: Searching for a specific value in a BST has an average time complexity of O(log n), where n is the number of nodes in the tree. This is much faster than searching for an element in an array or linked list, which have a time complexity of O(n) in the worst case.
- In-order traversal: BSTs can be traversed in-order, which visits the left subtree, the root, and the right subtree. This can be used to sort a dataset.
- Space efficient: BSTs are space efficient as they do not store any redundant information, unlike arrays and linked lists.
Disadvantages:
- Skewed trees: If a tree becomes skewed, the time complexity of search, insertion, and deletion operations will be O(n) instead of O(log n), which can make the tree inefficient.
- Additional time required: Self-balancing trees require additional time to maintain balance during insertion and deletion operations.
- Efficiency: BSTs are not efficient for datasets with many duplicates as they will waste space.
FAQ’s (Frequently asked questions) on Binary Search Tree:
1. What is a Binary Search Tree?
A binary search tree (BST) is a binary tree where every node in the left subtree is less than the root, and every node in the right subtree is of a value greater than the root. The properties of a binary search tree are recursive: if we consider any node as a “root,” these properties will remain true.
2. What is the Binary Search Tree Operation?
There are major three operations in Binary Search Tree: 1. Insertion, 2. Deletion, 3. Searching. Because of its properties its efficient to search any element in Binary Search Tree.
3. What is Binary Search Tree and AVL tree?
Binary Search Tree: A binary search tree (BST) is a binary tree where every node in the left subtree is less than the root, and every node in the right subtree is of a value greater than the root.
AVL Tree: Binary search trees (BSTs) that self-balance and rotate automatically are known as AVL trees.
4. What are the uses of Binary Search Tree?
Binary search trees can be used to implement abstract data types such as dynamic sets, lookup tables and priority queues, and used in sorting algorithms such as tree sort.
5. What is the difference between binary search tree and binary tree ?
A Binary search tree is a tree that follows some order to arrange the elements, whereas the binary tree does not follow any order.
Related Articles:
Share your thoughts in the comments
Please Login to comment...