Trigonometric Identities Class 10

Trigonometric Identities are the rules that are followed by the Trigonometric Ratios. Trigonometric Identities and ratios are the fundamentals of trigonometry. Trigonometry is used in various fields for different calculations. The trigonometric identities class 10 gives the connection between the different trigonometric ratios. This article covers trigonometric identities class 10 in addition to their proofs.

This article will be extremely helpful for class 10 students for their exams. Also, we will solve some examples of trigonometric identities Class 10. Let’s discuss the topic of Trigonometric Identities Class 10 in depth.

What are Trigonometric Identities?

The identities which provide the relation between the different trigonometric ratios are called Trigonometric Identities. In class 10, the trigonometric identities relate all the trigonometric ratios with each other. The trigonometric identities class 10 includes three trigonometric identities. Below we will study the trigonometric identities of class 10.

What are Trigonometric Ratios?

There are six basic trigonometric ratios namely, sin, cos, tan, sec, cosec and cot. The formulas of these basic trigonometric ratios are listed below:

• Sin θ = Perpendicular / Hypotenuse
• Cos θ = Base / Hypotenuse
• Tan θ = Sin θ / Cos θ = Perpendicular / Base
• Cosec θ = 1 / Sin θ = Hypotenuse / Perpendicular
• Sec θ = 1 / Cos θ = Hypotenuse / Base
• Cot θ = 1 / Tan θ = Base / Perpendicular

List of All Trigonometric Identities Class 10

The three basic trigonometric identities are listed below:

• sin²θ + cos²θ = 1
• 1 + tan²θ = sec²θ
• 1 + cot²θ = cosec²θ

Some Other Trigonometric Identities Class 10

Other then Pythagorean identities there are some more identities discussed in class 10. These identities are:

Reciprocal Identities

• cosec θ = 1/sin θ
• sec θ = 1/cos θ
• cot θ = 1/tan θ

Quotient Identities

• tan θ = sin θ/cos θ
• cot θ = cos θ/sin θ

Learn more about Trigonometrtic Identities

Proof of Trigonometric Identities Class 10

In this section we will prove trigonometric identities class 10 that are mentioned above.

Consider a right-angled triangle PQR.

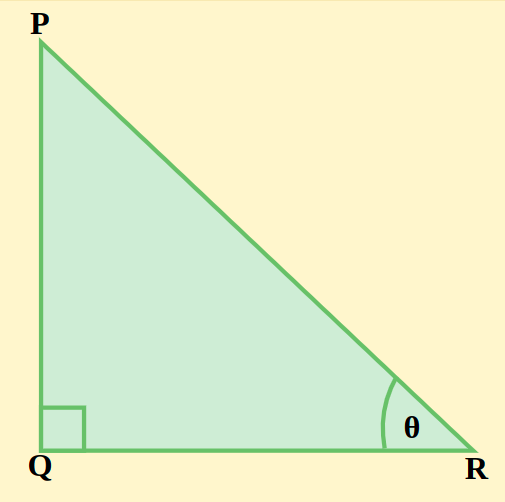
By Pythagoras theorem

PR² = PQ² + QR² – – -(1)

Proof of sin²θ + cos²θ = 1

Dividing equation (1) by PR²

1 = PQ²/PR² + QR²/PR²

⇒ 1 = (PQ/PR)² + (QR/PR)² – – -(2)

In right-angled triangle PQR

PQ/PR = sin θ

and QR/PR = cos θ

Put value of PQ/PR and QR/PR in equation (2), we get

sin²θ + cos²θ = 1

Hence proved.

Proof of 1 + tan²θ = sec²θ

Dividing equation (1) by QR²

PR²/QR²= PQ²/QR² + 1

⇒ (PR/QR)² = (PQ/QR)² + 1 – – -(3)

In right-angled triangle PQR

PR/QR = sec θ

and PQ/QR = tan θ

Put value of PR/QR and PQ/QR in equation (3), we get

1 + tan²θ = sec²θ

Hence proved.

Proof of 1 + cot²θ = cosec²θ

Dividing equation (1) by PQ²

(PR²/PQ²) = 1 + (QR²/PQ²)

(PR/PQ)² = 1 + (QR/PQ)² – – – (4)

In right-angled triangle PQR

PR/PQ = cosec θ

and QR/PQ = cot θ

Put value of PR/PQ and QR/PQ in equation (4), we get

1 + cot²θ = cosec²θ

Hence proved.

Trigonmetric Identities Class 10 Table

Identities Name	Identities
Pythagorean Identities	sin2θ + cos2θ = 1
	1 + tan2θ = sec2θ
	1 + cot2θ = cosec2θ
Reciprocal Identities	cosec θ = 1/sin θ
	sec θ = 1/cos θ
	cot θ = 1/tan θ
Quotient Identities	tan θ = sin θ/cos θ
	cot θ = cos θ/sin θ

Solved Examples on Trigonometric Identities Class 10

Example 1: Prove that: (1 + cot²A) sin²A = 1

Solution:

LHS = (1 + cot²A) sin²A

Using trigonometric identity

1 + cot²θ = cosec²θ

⇒ LHS = cosec²A sin²A

⇒ LHS = (1 / sin²A) sin²A [cosec A = 1 / sin A]

⇒ LHS = 1

Thus, LHS = RHS

Hence Proved

Example 2: Prove that: tan²B cos²B = 1 – cos²B

Solution:

LHS = tan²B cos²B

Using trigonometric identity

⇒ 1 + tan²θ = sec²θ

⇒ tan²θ = sec²θ – 1

⇒ LHS = (sec²B – 1) cos²B

⇒ LHS = sec²Bcos²B – cos²B

⇒ LHS = [(1/ cos²B)cos²B] – cos²B

⇒ LHS = 1 – cos²B

Thus, LHS = RHS

Hence Proved

Example 3: Prove that: tan θ + (1/tan θ) = sec θ cosec θ

Solution:

LHS = tan θ + (1/tan θ)

⇒ LHS = (tan²θ + 1)/tan θ

Using trigonometric identity

1 + tan²θ = sec²θ

⇒ LHS = sec²θ/tanθ

⇒ LHS = (1 / cos²θ) × (cos θ / sinθ )

⇒ LHS = (1 / cos θ) × (1 / sin θ)

⇒ LHS = sec θ cosec θ [sec θ = 1/cos θ and cosec θ = 1/sin θ]

Thus, LHS = RHS

Hence Proved

Example 4: Prove that: √[(1 – cos θ)/(1 + cos θ)] = cosec θ – cot θ

Solution:

LHS = √[(1 – cos θ)/(1 + cos θ)]

⇒ LHS = √[{(1 – cos θ)/(1 + cos θ)} × {(1 – cos θ) / (1 – cos θ)}]

⇒ LHS = √[(1 – cos θ)²/(1 – cos²θ)]

Using trigonometric identity

sin²θ + cos²θ = 1

⇒ LHS = √[(1 – cosθ)² / sin²θ]

⇒ LHS = (1 – cos θ) / sin θ

⇒ LHS = (1 / sin θ) – (cos θ / sin θ)

⇒ LHS = cosec θ – cot θ [cotθ = cosθ / sinθ and cosecθ = 1/sinθ]

Thus, LHS = RHS

Hence Proved

Example 5: Prove that: sin θ / (1 – cos θ) = cosec θ + cot θ

Solution:

LHS = sin θ/(1 – cos θ)

⇒ LHS = [sin θ/(1 – cos θ)] × [(1 + cos θ)/(1 + cos θ)}]

⇒ LHS = [sin θ (1 + cos θ)] / (1 – cos²θ)

Using trigonometric identity

sin²θ + cos²θ = 1

⇒ LHS = [sin θ (1 + cos θ)] / sin²θ

⇒ LHS = (1 + cos θ)/sin θ

⇒ LHS = (1 / sin θ) + (cos θ/sinθ)

⇒ LHS = cosec θ + cot θ [cot θ = cos θ/sin θ and cosec θ = 1/sin θ]

Thus, LHS = RHS

Hence Proved

Example 6: Prove that: [(1 + cot²θ)tan θ]/sec²θ = cot θ

Solution:

LHS = [(1 + cot²θ)tan θ]/sec²θ

Using trigonometric identity

1 + cot²θ = cosec²θ

⇒ LHS = [cosec²θ tan θ]/sec²θ

⇒ LHS = (1/sin²θ) × (sin θ/cos θ) × (cos²θ/1)

⇒ LHS = (cos θ/ sin θ)

⇒ LHS = cot θ [cot θ = cos θ/sinθ]

Thus, LHS = RHS

Hence Proved

Practice Questions on Trigonometric Identities Class 10

Q1. Prove that: cosecθ√[(1 – cos²θ) = 1

Q2. Prove that: (sec²x – 1)(cosec²x – 1) = 1

Q3. Prove that: sin²C + [1 / (1 + tan²C)] = 1

Q4. Prove that: sec A (1 – sin A) (sec A + tan A) = 1

Q5. Prove that: (1 – sin θ) / (1 + sin θ) = (sec θ – tanθ)²

Q6. Prove that: (cosec θ + sin θ)(cosec θ – sin θ) = cot²θ + cos²θ

Trigonometric Identities Class 10 – FAQs

1. What are Trigonometric Identities?

The trigonometric identities are the identities which gives the connection between the trigonometric identities.

2. List the Three basic Trigonometric Identities in Class 10.

The three basic trigonometric identities are:

• sin²θ + cos²θ = 1
• 1 + tan²θ = sec²θ
• 1 + cot²θ = cosec²θ

3. What are the Six Trigonometric Ratios?

The six basic trigonometric ratios are: sin, cos, tan, cosec, sec and cot.

4. How to Prove Trigonometric Identities Class 10?

To prove trigonometric identities class 10 we use Pythagoras theorem. The detailed proof has been discuseed in the article above.

5. Is Trigonometric Identities Class 10 Important?

Yes, Trigonometric Identities Class 10 is extremely important for board exams as well as for building strong foundation in Trigonometry