Total number of divisors for a given number

Given a positive integer n, we have to find the total number of divisors for n.

Examples:

Input : n = 25
Output : 3
Divisors are 1, 5 and 25.

Input : n = 24
Output : 8
Divisors are 1, 2, 3, 4, 6, 8
12 and 24.

We have discussed different approaches for printing all divisors (here and here). Here the task is simpler, we need to count divisors.
First of all store all primes from 2 to max_size in an array so that we should only check for the prime divisors. Now we will only wish to calculate the factorization of n in the following form:
n =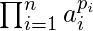
=
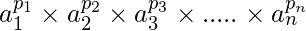where a_i are prime factors and p_i are integral power of them.
So, for this factorization we have formula to find total number of divisor of n and that is:

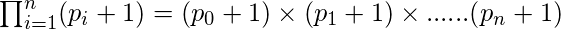
C++

// CPP program for finding number of divisor
#include <bits/stdc++.h>

using namespace std;

// program for finding no. of divisors
int divCount(int n)
{
    // sieve method for prime calculation
    bool hash[n + 1];
    memset(hash, true, sizeof(hash));
    for (int p = 2; p * p < n; p++)
        if (hash[p] == true)
            for (int i = p * 2; i < n; i += p)
                hash[i] = false;

    // Traversing through all prime numbers
    int total = 1;
    for (int p = 2; p <= n; p++) {
        if (hash[p]) {

            // calculate number of divisor
            // with formula total div =
            // (p1+1) * (p2+1) *.....* (pn+1)
            // where n = (a1^p1)*(a2^p2)....
            // *(an^pn) ai being prime divisor
            // for n and pi are their respective
            // power in factorization
            int count = 0;
            if (n % p == 0) {
                while (n % p == 0) {
                    n = n / p;
                    count++;
                }
                total = total * (count + 1);
            }
        }
    }
    return total;
}

// driver program
int main()
{
    int n = 24;
    cout << divCount(n);
    return 0;
}

Java

// Java program for finding
// number of divisor
import java.io.*;
import java.util.*;
import java.lang.*;

class GFG
{
// program for finding
// no. of divisors
static int divCount(int n)
{
    // sieve method for prime calculation
    boolean hash[] = new boolean[n + 1];
    Arrays.fill(hash, true);
    for (int p = 2; p * p < n; p++)
        if (hash[p] == true)
            for (int i = p * 2; i < n; i += p)
                hash[i] = false;

    // Traversing through
    // all prime numbers
    int total = 1;
    for (int p = 2; p <= n; p++)
    {
        if (hash[p])
        {

            // calculate number of divisor
            // with formula total div =
            // (p1+1) * (p2+1) *.....* (pn+1)
            // where n = (a1^p1)*(a2^p2)....
            // *(an^pn) ai being prime divisor
            // for n and pi are their respective
            // power in factorization
            int count = 0;
            if (n % p == 0)
            {
                while (n % p == 0)
                {
                    n = n / p;
                    count++;
                }
                total = total * (count + 1);
            }
        }
    }
    return total;
}

// Driver Code
public static void main(String[] args)
{
    int n = 24;
    System.out.print(divCount(n));
}
}

// This code is contributed
// by Akanksha Rai(Abby_akku)

Python3

# Python3 program for finding
# number of divisor

# program for finding
# no. of divisors
def divCount(n):

    # sieve method for
    # prime calculation
    hh = [1] * (n + 1);

    p = 2;
    while((p * p) < n):
        if (hh[p] == 1):
            for i in range((p * 2), n, p):
                hh[i] = 0;
        p += 1;

    # Traversing through
    # all prime numbers
    total = 1;
    for p in range(2, n + 1):
        if (hh[p] == 1):

            # calculate number of divisor
            # with formula total div =
            # (p1+1) * (p2+1) *.....* (pn+1)
            # where n = (a1^p1)*(a2^p2)....
            # *(an^pn) ai being prime divisor
            # for n and pi are their respective
            # power in factorization
            count = 0;
            if (n % p == 0):
                while (n % p == 0):
                    n = int(n / p);
                    count += 1;
                total *= (count + 1);

    return total;

# Driver Code
n = 24;
print(divCount(n));

# This code is contributed by mits

C#

// C# program for finding
// number of divisor
using System;

class GFG
{
// program for finding
// no. of divisors
static int divCount(int n)
{
    // sieve method for prime calculation
    bool[] hash = new bool[n + 1];
    for (int p = 2; p * p < n; p++)
        if (hash[p] == false)
            for (int i = p * 2;
                     i < n; i += p)
                hash[i] = true;

    // Traversing through
    // all prime numbers
    int total = 1;
    for (int p = 2; p <= n; p++)
    {
        if (hash[p] == false)
        {

            // calculate number of divisor
            // with formula total div =
            // (p1+1) * (p2+1) *.....* (pn+1)
            // where n = (a1^p1)*(a2^p2)....
            // *(an^pn) ai being prime divisor
            // for n and pi are their respective
            // power in factorization
            int count = 0;
            if (n % p == 0)
            {
                while (n % p == 0)
                {
                    n = n / p;
                    count++;
                }
                total = total * (count + 1);
            }
        }
    }
    return total;
}

// Driver Code
public static void Main()
{
    int n = 24;
    Console.WriteLine(divCount(n));
}
}

// This code is contributed
// by mits

PHP

<?php
// PHP program for finding
// number of divisor

// program for finding
// no. of divisors
function divCount($n)
{
    // sieve method for
    // prime calculation
    $hash = array_fill(0, $n + 1, 1);

    for ($p = 2;
        ($p * $p) < $n; $p++)
        if ($hash[$p] == 1)
            for ($i = ($p * 2);
                 $i < $n; $i= ($i + $p))
                $hash[$i] = 0;

    // Traversing through
    // all prime numbers
    $total = 1;
    for ($p = 2; $p <= $n; $p++)
    {
        if ($hash[$p] == 1)
        {

            // calculate number of divisor
            // with formula total div =
            // (p1+1) * (p2+1) *.....* (pn+1)
            // where n = (a1^p1)*(a2^p2)....
            // *(an^pn) ai being prime divisor
            // for n and pi are their respective
            // power in factorization
            $count = 0;
            if ($n % $p == 0)
            {
                while ($n % $p == 0)
                {
                    $n = ($n / $p);
                    $count++;
                }
                $total = $total *
                        ($count + 1);
            }
        }
    }
    return $total;
}

// Driver Code
$n = 24;
echo divCount($n);

// This code is contributed by mits
?>

Javascript

<script>

// Javascript program for finding number of divisor

// program for finding no. of divisors
function divCount(n)
{
    // sieve method for prime calculation
    var hash = Array(n+1).fill(true);
    for (var p = 2; p * p < n; p++)
        if (hash[p] == true)
            for (var i = p * 2; i < n; i += p)
                hash[i] = false;

    // Traversing through all prime numbers
    var total = 1;
    for (var p = 2; p <= n; p++) {
        if (hash[p]) {

            // calculate number of divisor
            // with formula total div =
            // (p1+1) * (p2+1) *.....* (pn+1)
            // where n = (a1^p1)*(a2^p2)....
            // *(an^pn) ai being prime divisor
            // for n and pi are their respective
            // power in factorization
            var count = 0;
            if (n % p == 0) {
                while (n % p == 0) {
                    n = parseInt(n / p);
                    count++;
                }
                total = total * (count + 1);
            }
        }
    }
    return total;
}

// driver program
var n = 24;
document.write( divCount(n));

</script>

Output:

8

Reference : Number of divisors.
This article is contributed by Shivam Pradhan (anuj_charm). If you like GeeksforGeeks and would like to contribute, you can also write an article using contribute.geeksforgeeks.org or mail your article to contribute@geeksforgeeks.org. See your article appearing on the GeeksforGeeks main page and help other Geeks.
Please write comments if you find anything incorrect, or you want to share more information about the topic discussed above.