Divisors of n-square that are not divisors of n
Last Updated :
07 Aug, 2022
Given an positive large integer n. Count the number of positive divisors of n2 which are not divisible by any divisor of n(1 <= n <= 1012).
Input: 6
Output: 5
Explanation
Total divisors of 62 are 9 i.e.,
1, 2, 3, 4, 6, 9, 12, 18, 36
Total divisors of '6' are 4,
1, 2, 3, 6
Total divisor of '36' which are not
divisible by divisors of '6' are
'5' i.e., 4, 9, 12, 18, 36
Input: 8
Output: 3
Simple approach is to traverse for every divisor of n2 and count only those divisors which are not divisor of ‘n’. Time complexity of this approach is O(n).
Efficient approach is to use prime factorization to count total divisors of n2. A number ‘n’ can be represented as product of primes 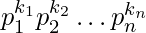 . Refer this to understand more.
. Refer this to understand more.
Let 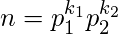 for some primes p1 and p2.Squaring both the sides
for some primes p1 and p2.Squaring both the sides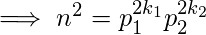 Total factors of n2 will be,
Total factors of n2 will be,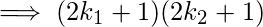 Total factors of 'n' will be,
Total factors of 'n' will be,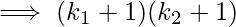 Difference between the two gives the requiredanswer
Difference between the two gives the requiredanswer
C++
#include <bits/stdc++.h>
using namespace std;
int factors(long long n)
{
unordered_map<int, int> prime;
for (int i = 2; i <= sqrt(n); ++i) {
while (n % i == 0) {
++prime[i];
n = n / i;
}
}
if (n > 2)
++prime[n];
int ans1 = 1, ans2 = 1;
for (auto it : prime) {
ans1 *= 2 * it.second + 1;
ans2 *= it.second + 1;
}
return ans1 - ans2;
}
int main()
{
long long n = 5;
cout << factors(n) << endl;
n = 8;
cout << factors(n);
return 0;
}
|
Java
import java.util.*;
class GFG
{
static int factors(int n)
{
HashMap<Integer,
Integer>prime = new HashMap<Integer,
Integer>();
for (int i = 2; i <= Math.sqrt(n); ++i)
{
while (n % i == 0)
{
if (prime.containsKey(i))
{
prime.put(i, prime.get(i) + 1);
}
else
{
prime.put(i, 1);
}
n = n / i;
}
}
if (n > 2)
{
if(prime.containsKey(n))
{
prime.put(n, prime.get(n) + 1);
}
else
{
prime.put(n, 1);
}
}
int ans1 = 1, ans2 = 1;
for (Map.Entry<Integer,
Integer> it : prime.entrySet())
{
ans1 *= 2 * it.getValue() + 1;
ans2 *= it.getValue() + 1;
}
return ans1 - ans2;
}
public static void main(String[] args)
{
int n = 5;
System.out.println(factors(n));
n = 8;
System.out.println(factors(n));
}
}
|
Python3
import math as mt
def factors(n):
prime = dict()
for i in range(2, mt.ceil(mt.sqrt(n + 1))):
while (n % i == 0):
if i in prime.keys():
prime[i] += 1
else:
prime[i] = 1
n = n // i
if (n > 2):
if n in prime.keys():
prime[n] += 1
else:
prime[n] = 1
ans1 = 1
ans2 = 1
for it in prime:
ans1 *= 2 * prime[it] + 1
ans2 *= prime[it] + 1
return ans1 - ans2
n = 5
print(factors(n))
n = 8
print(factors(n))
|
C#
using System;
using System.Collections.Generic;
class GFG
{
static int factors(int n)
{
Dictionary<int,
int> prime = new Dictionary<int,
int>();
for (int i = 2; i <= Math.Sqrt(n); ++i)
{
while (n % i == 0)
{
if (prime.ContainsKey(i))
{
prime[i] = prime[i] + 1;
}
else
{
prime.Add(i, 1);
}
n = n / i;
}
}
if (n > 2)
{
if(prime.ContainsKey(n))
{
prime[n] = prime[n] + 1;
}
else
{
prime.Add(n, 1);
}
}
int ans1 = 1, ans2 = 1;
foreach(KeyValuePair<int, int> it in prime)
{
ans1 *= 2 * it.Value + 1;
ans2 *= it.Value + 1;
}
return ans1 - ans2;
}
public static void Main(String[] args)
{
int n = 5;
Console.WriteLine(factors(n));
n = 8;
Console.WriteLine(factors(n));
}
}
|
Javascript
<script>
function factors(n)
{
let prime = new Map();
for (let i = 2; i <= Math.sqrt(n); ++i)
{
while (n % i == 0)
{
if (prime.has(i))
{
prime.set(i, prime.get(i) + 1);
}
else
{
prime.set(i, 1);
}
n = Math.floor(n / i);
}
}
if (n > 2)
{
if(prime.has(n))
{
prime.set(n, prime.get(n) + 1);
}
else
{
prime.set(n, 1);
}
}
let ans1 = 1, ans2 = 1;
for (let [key, value] of prime.entries())
{
ans1 *= 2 * value + 1;
ans2 *= value + 1;
}
return ans1 - ans2;
}
let n = 5;
document.write(factors(n)+"<br>");
n = 8;
document.write(factors(n)+"<br>");
</script>
|
Time complexity: O(log(n))
Auxiliary space: O(n) as using unordered_map
Share your thoughts in the comments
Please Login to comment...