CBSE Class 10 Maths Notes Chapter 13 Surface Areas and Volumes are an excellent resource, for knowing all the concepts of a particular chapter in a crisp, and friendly manner. Our articles, help students learn in their language, with proper images, and solved examples for better understanding the concepts.
Chapter 13 of the NCERT Class 10 Maths textbook delves into the world of Surface area and volume and covers various topics such as understanding the CSA, TSA of combined solids, volume of combined solids, converting from one solid to another solid, and the volume of the frustum. Notes are designed to give students a comprehensive summary of the entire chapter and include all the essential topics, formulae, and concepts needed to succeed in their exams.
Need of Studying Surface Areas and Volumes
Surface areas and volumes play a significant role, in our day-to-day life. Look at your phone, it’s a cuboid, with blunt edges. Look at your room, it may be a cube or a cuboid, an oil-carrying tank is the combination of 2 hemispheres and a cylinder, a birthday cap it’s a cone, an aluminium bucket it’s a frustum, etc. So, unknowingly we have been surrounded, by many solids, which are combinations of some simple solids. Hence, this chapter will help us know how to calculate the surface area and volumes of the combination of figures.
Before moving toward the solids, we need to revise some of the terminologies which have already been discussed in the 9th class.
Lateral Surface Area
Lateral surface area is the area of a solid, in which the area of the top, and the area of the base are excluded. It is for solids like cubes, and cuboids, which have no curved surfaces. For example, a cube has a total surface area of 6πr2, and a lateral surface area is 4πr2 because the upper and the lower sides of the cube are excluded.
Curved Surface Area
Curved surface area is the area of a solid, in which the area of the top, and the area of the base are excluded. It is for solids like cylinders, cones, etc. For example, the total surface area of a cylinder is 2πr2 + 2πrh, and the curved surface area is 2πrh because the top and the bottom circular area have been excluded.
Note: The curved surface area of the solid changes, if the shape of the solid changes.
Total Surface Area
Total surface area is the total outer area, a solid occupies. For example, the total surface area of the cone is equal to the curved surface area of the cone and the area of the circular base i.e. πrl + πr2.
Note: The total surface area of the solid changes, if the shape of the solid changes.
Volume
Volume is the space occupied by a solid. For example, the volume of the cube is a3, the volume of the cylinder is πr2h, etc.
Note: Volume of the solid do not change, on changing the shape of the solid.
Also, Read
Surface Area and Volume of the Simple Solids
We had a detailed talk about the surface area and volume of simple solids, in class 9th. This chapter focuses on the surface areas and volumes of the combined solids. To know more about this topic read surface area and volume. The below table shows the summary of formulas studied in class 9th of the simple solids.
| Solid | Curved
Surface Area
| Total
Surface Area
| Volume |
|---|
| Cube | 4a2 | 6a2 | a3 |
|---|
| Cuboid | 2(l + b)h | 2(lb + bh + lh) | lbh |
|---|
| Cone | πrl | πr(r + l) | 1/3πr2h |
|---|
| Cylinder | 2πrh | 2πr(r + h) | πr2h |
|---|
| Sphere | 4πr2 | 4πr2 | 4/3πr3 |
|---|
| Hemisphere | 2πr2 | 3πr2 | 2/3πr3 |
|---|
| Spherical Shell | 4πR2 (Outer)
4πr2 (Inner)
| 4πR2 + 4πr2 | 4/3π(R3 – r3) |
|---|
| Frustum | π(r1 + r2)l | π(r1 + r2)l + π(r12 + r22) | (1/3)πh(r12 + r22 + r1r2) |
|---|
Surface Area of Combination of Solids
Combination of solids means combining many simple solids, of which area and volume are known to us. Whenever we combine many solids, then we always arrive at two cases:
Case 1
On combining solids, no area in the resultant solid hides another solid area. Hence, the area of the combined solid is equal to the area of the individual/simple solids.
Surface area of the combined solid = surface area of simple solid 1 + surface area of the simple solid 2 + ….
Example: Given the figure below, the radius of the hemisphere is 2cm, and the total width of the solid is 7cm. Find the total surface area of the solid.
Solution:
We can observe that,
The combined figure, is made from 2 hemispheres and 1 cylinder.
Hence,
Surface area of the solid = 2 * (CSA of Hemisphere) + CSA of Cylinder
radius = r = 2cm,
Height of the cylinder = h = total width of solid – 2 * r
Height of the cylinder = h = 7 – 2 * 2 = 3cm,
CSA of Hemisphere = 2πr2 = 2π22 = 8π
CSA of Cylinder = 2πrh = 2π.2.3 = 12π
Surface area of the solid = 2 * 8π + 12π = 28π cm2.
Case 2
It is also possible that, on combining simple solids, the resultant solid formed might have some hide some area, of a simple solid. Hence, the area of the combined solid is equal to the area of the individual/simple solid, subtracting the hidden area in the combined solid.
Surface area of the combined solid = surface area of the simple solids – area of the hidden solids
Example: A cone of slant height 2cm, with a radius of 1cm, is placed on the top of a square of dimensions 2 x 2 x 2 cm. Find the surface area of the combined solid.
Solution:
Given,
l = 2cm, r = 1cm, a = 2cm,
Surface area of the solid = surface area of cube + surface area of cone – area of circle(hidden area)
Surface area of cube = 6a2 = 6.22 = 24cm2,
Surface area of cone = πrl = π.1.2 = 2π
Area of circle(hidden area) = πr2 = π.12 = π
Surface area of the solid = 24 + 2π – π = 24 + π
Hence, the surface area of the solid is (24 + π) cm2.
Also, Read
Volume of the Combination of Solids
As volume refers to the capacity or the space occupied, we can infer that the volume of the combination of solids is equal to the sum of the volume of the simple solids. This was not the case with surface areas, where some part of the simple solid, gets hidden.
Volume of the combination of the solids = volume of the simple solid 1 + volume of the simple solid 2 + volume of the simple solid 3 + …
Example: Given an ice cream cone, as shown below. The total height of the ice cream cone is 7cm, and the width is 6cm. Find the volume of the ice cream cone.
Solution:
We can observe that,
The ice cream cone is made of 2 simple solids i.e. a cone and a hemisphere.
Volume of ice cream cone = volume of cone + volume of hemisphere,
Given,
Raidus of the hemisphere and base of the cone = r = 3cm,
Height of cone = Total height of solid – radius of the hemisphere = h = 7 – 3 = 4cm,
Volume of hemisphere = 2/3πr3 = 2/3.π.33 = 18π cm2,
Volume of cone = 1/3πr2h = 1/3π324 = 12π cm2,
Volume of ice cream cone = 18π + 12π = 30π cm2.
Conversion of solid from one Shape to another
Volume refers to the space occupied by a solid or the matter/capacity of that solid. Now, let us take an example of clay to understand better the concept of conversion of solids, Clay can be changed to any shape, but on changing the shape is outer surface area changes, but the volume remains the same. Let us take one more example, if a container of a particular shape, has 100L water in it, then, if we pour the same water into another container, of a different shape, then, also we have 100L water in it.
Volume of Solid before Changing Form = Volume of Solid after Changing Form
Example: A cone of height 12 cm and radius of base 3 cm is made up of modelling clay. A child reshapes it in the form of a sphere. Find the radius of the sphere.
Solution:
We know that,
Volume of cone = Volume of Sphere …(1)
Volume of cone = 1/3πr2h
Volume of cone = 1/3π(3)212
Volume of cone = 36π cm3 … (2)
Volume of Sphere = 4/3πr3 …(3)
Putting values of (2) and (3), in (1),
36π = 4/3πr3,
On solving,
r = 3cm,
Hence, the radius of the sphere is 3 cm.
Frustum of a Cone
In 9th class, we have not read about the frustum of a cone. If a cone is cut into two halves, horizontally, then, the lower remaining portion of the cone is called frustum. The front view of the frustum is equivalent to the trapezium.
Given a frustum, with a smaller radius as r1, and a larger radius as r2, height h, and the slant height = l. The curved surface area, total surface area, and volume of the frustum are given below(the proof of these formulas, is outside the scope of our syllabus):
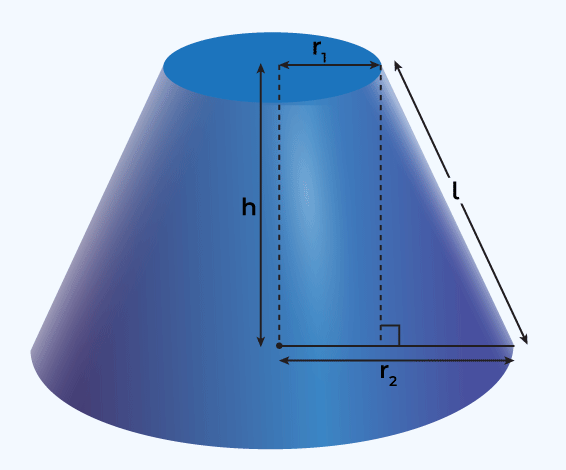
Curved Surface Area of the Frustum
The curved surface area of a frustum can be calculated using the formula:
CSA = π(r₁ + r₂)l
Where,
- π is a mathematical constant ≈ 3.14,
- r1 is the radius of the larger base of the frustum,
- r2 is the radius of the smaller base of the frustum,
- l is the slant height of the frustum.
Where slant height l can be given as
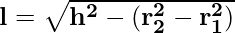
Where h is the height of the frustum.
Total Surface Area of the Frustum
The curved surface area of a frustum can be calculated using the formula:
TSA = π(r1 + r2)l + π(r12 + r22)
Where,
- π is a mathematical constant ≈ 3.14,
- r1 is the radius of the larger base of the frustum,
- r2 is the radius of the smaller base of the frustum,
- l is the slant height of the frustum.
Volume of the Frustum
The volume of the Frustum is given by the following formula:
Volume = 1/3πh(r12 + r22 + r1r2)
Where,
- π is a mathematical constant ≈ 3.14,
- h is the height of the frustum,
- r1 is the radius of the larger base of the frustum,
- r2 is the radius of the smaller base of the frustum,
- l is the slant height of the frustum.
Example 1: Given a frustum of the cone, where the smaller radius is 2 cm, the larger radius is 4 cm, and the height of the frustum is 3 cm. Find the volume of the frustum of the cone.
Solution:
Given, r1 = 2cm, r2 = 4cm, h = 3cm,
Volume of the frustum of the cone = 1/3πh(r12 + r22 + r1r2),
⇒ 1/3π.3.(22 + 42 + 2.4),
⇒ 28π cm3
Volume of the frustum of the cone is 28π cm3.
Example 2: An open metal bucket is in the shape of a frustum of a cone, mounted on a hollow cylindrical base made of the same metallic sheet. The diameters of the two circular ends of the bucket are 45 cm and 25 cm, the total vertical height of the bucket is 40 cm and that of the cylindrical base is 6 cm. Find the area of the metallic sheet used to make the bucket, where we do not take into account the handle of the bucket.
Solution:
Given,
Total height of the bucket = 40cm,
Larger radii = r1 = 45/2 = 22.5cm,
Smaller radii = r2 = 25/2 = 12.5cm,
Height of the cylinder = h1 = 6cm,
Radius of the cylinder = radius of the smaller circle of the frustum = 12.5cm,
Radius of the circular base = radius of the smaller circle of the frustum = 12.5cm,
Height of the Frustum = Total height of the bucket – height of the cylinder,
Height of the Frustum = h = 40 – 6 = 34cm,
Total area of metallic sheet used to make the bucket = Surface area of the frustum + Area of the ciruclar base + Area of the cylinder, …(1)
Surface area of the frustum = π(r1 + r2)l = π(22.5 + 12.5)l,
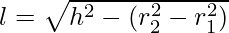
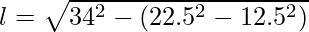
l = 35.44cm,
Put value of ‘l’ in the above equation,
Surface area of the frustum = π(35)(35.44) = 3894.56 cm2 …..(2)
Area of the circular base = πr12 = π(12.5)2 = 490.625 cm2 ……(3)
Area of the Cylinder = 2πr1h1 = 2π(12.5)(6) = 471 cm2 …..(4)
Put values of (2), (3), and (4) in equation (1),
Total area of metallic sheet used to make the bucket = 3894.56 + 490.625 + 471 = 4856.125 cm2
Also, Read
FAQs on NCERT Notes for Class 10 Maths Chapter 13 Surface Area and Volume
Q1: What is the difference between a cylinder and a cone?
Answer:
A cylinder has 2 circular surfaces parallel to each other joined by a curved surface, whereas a cone has 1 circular surface, which is joined to a single point.
Q2: What is the difference between surface area and volume?
Answer:
Surface area is the two-dimensional quantity that helps us calculate the area of the surface of any solid whereas volume is the three-dimensional quantity that helps us calculate the capacity of the solid.
Q3: How are the volume of the cone, and the volume of the cylinder related to each other?
Answer:
Volume of the Cone = 1/3πr2h,
Volume of the Cyliner = πr2h,
Hence, Volume of cone is 1/3rd of the volume of the cylinder.
Q4: What is the slant height of the frustum in terms of r1, r2, and h?
Answer:
Slant height of the frustum is given as:
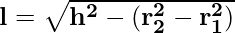
Where,
- r1 is the radius of the smaller circle,
- r2 is the radius of the larget circle,
- h is the class size.
Q5: What is a composite solid?
Solution:
A composite solid is the solid made of multiple well-defined solids.
Share your thoughts in the comments
Please Login to comment...