Sum of the series 1 + (1+2) + (1+2+3) + (1+2+3+4) + …… + (1+2+3+4+…+n)
Last Updated :
09 Sep, 2021
Given the value of n, we need to find the sum of the series where i-th term is sum of first i natural numbers.
Examples :
Input : n = 5
Output : 35
Explanation :
(1) + (1+2) + (1+2+3) + (1+2+3+4) + (1+2+3+4+5) = 35
Input : n = 10
Output : 220
Explanation :
(1) + (1+2) + (1+2+3) + .... +(1+2+3+4+.....+10) = 220
Naive Approach :
Below is implementation of above series :
C++
#include <bits/stdc++.h>
using namespace std;
int sumOfSeries(int n)
{
int sum = 0;
for (int i = 1 ; i <= n ; i++)
for (int j = 1 ; j <= i ; j++)
sum += j;
return sum;
}
int main()
{
int n = 10;
cout << sumOfSeries(n);
return 0;
}
|
Java
import java.util.*;
class GFG {
static int sumOfSeries(int n)
{
int sum = 0;
for (int i = 1 ; i <= n ; i++)
for (int j = 1 ; j <= i ; j++)
sum += j;
return sum;
}
public static void main(String[] args)
{
int n = 10;
System.out.println(sumOfSeries(n));
}
}
|
Python
def sumOfSeries(n):
return sum([i*(i+1)/2 for i in range(1, n + 1)])
if __name__ == "__main__":
n = 10
print(sumOfSeries(n))
|
C#
using System;
class GFG {
static int sumOfSeries(int n)
{
int sum = 0;
for (int i = 1; i <= n; i++)
for (int j = 1; j <= i; j++)
sum += j;
return sum;
}
public static void Main()
{
int n = 10;
Console.Write(sumOfSeries(n));
}
}
|
PHP
<?php
function sumOfSeries($n)
{
$sum = 0;
for ($i = 1 ; $i <= $n ; $i++)
for ($j = 1 ; $j <= $i ; $j++)
$sum += $j;
return $sum;
}
$n = 10;
echo(sumOfSeries($n));
?>
|
Javascript
<script>
function sumOfSeries(n)
{
let sum = 0;
for (let i = 1 ; i <= n ; i++)
for (let j = 1 ; j <= i ; j++)
sum += j;
return sum;
}
let n = 10;
document.write(sumOfSeries(n));
</script>
|
Output :
220
Efficient Approach :
Let 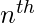 term of the series 1 + (1 + 2) + (1 + 2 + 3) + (1 + 2 + 3 + 4)…(1 + 2 + 3 +..n) be denoted as an
term of the series 1 + (1 + 2) + (1 + 2 + 3) + (1 + 2 + 3 + 4)…(1 + 2 + 3 +..n) be denoted as an
an = Σn1 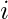 =
= 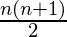 =
= 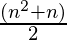 Sum of n-terms of series
Σn1 an = Σn1
Sum of n-terms of series
Σn1 an = Σn1 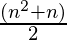 =
= 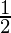 Σ
Σ 
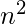
![Rendered by QuickLaTeX.com ]](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-3bd5d776ed7afadcef473636fc1fe45f_l3.png) + Σ
+ Σ 
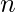
![Rendered by QuickLaTeX.com ]](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-3bd5d776ed7afadcef473636fc1fe45f_l3.png) =
= 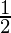 *
* 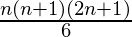 +
+ 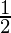 *
* 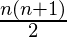 =
= 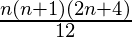
Below is implementation of above approach :
C++
#include <bits/stdc++.h>
using namespace std;
int sumOfSeries(int n)
{
return (n * (n + 1) * (2 * n + 4)) / 12;
}
int main()
{
int n = 10;
cout << sumOfSeries(n);
}
|
Java
import java.util.*;
class GFG {
static int sumOfSeries(int n)
{
return (n * (n + 1) *
(2 * n + 4)) / 12;
}
public static void main(String[] args)
{
int n = 10;
System.out.println(sumOfSeries(n));
}
}
|
Python
def sumOfSeries(n):
return (n * (n + 1) * (2 * n + 4)) / 12;
if __name__ == '__main__':
n = 10
print(sumOfSeries(n))
|
C#
using System;
class GFG {
static int sumOfSeries(int n)
{
return (n * (n + 1) * (2 * n + 4)) / 12;
}
public static void Main()
{
int n = 10;
Console.Write(sumOfSeries(n));
}
}
|
PHP
<?php
function sumOfSeries($n)
{
return ($n * ($n + 1) *
(2 * $n + 4)) / 12;
}
$n = 10;
echo(sumOfSeries($n));
?>
|
Javascript
<script>
function sumOfSeries(n)
{
return (n * (n + 1) *
(2 * n + 4)) / 12;
}
let n = 10;
document.write(sumOfSeries(n));
</script>
|
Output :
220
Time Complexity: O(1)
Auxiliary Space: O(1)
Share your thoughts in the comments
Please Login to comment...