Sum of alternating sign Squares of first N natural numbers
Last Updated :
08 Apr, 2021
Given a number N, the task is to find the sum of alternating sign squares of first N natural numbers, i.e.,
12 – 22 + 32 – 42 + 52 – 62 + ….
Examples:
Input: N = 2
Output: 5
Explanation:
Required sum = 12 - 22 = -1
Input: N = 8
Output: 36
Explanation:
Required sum
= 12 - 22 + 32 - 42 + 52 - 62 + 72 - 82
= 36
Naive approach: O(N)
The Naive or Brute force approach to solve this problem states to find the square of each number from 1 to N and add them with alternating sign in order to get the required sum.
- For each number in 1 to N, find its square
- Add these squares with alternating sign
- This would give the required sum.
Below is the implementation of the above approach:
C++
#include <iostream>
using namespace std;
int summation(int n)
{
int sum = 0;
for (int i = 1; i <= n; i++) {
if (i % 2 == 1)
sum += (i * i);
else
sum -= (i * i);
}
return sum;
}
int main()
{
int N = 2;
cout << summation(N);
return 0;
}
|
Java
class GFG
{
static int summation(int n)
{
int sum = 0;
for (int i = 1; i <= n; i++) {
if (i % 2 == 1)
sum += (i * i);
else
sum -= (i * i);
}
return sum;
}
public static void main (String[] args)
{
int N = 2;
System.out.println(summation(N));
}
}
|
Python3
def summation(n) :
sum = 0;
for i in range(1, n + 1) :
if (i % 2 == 1) :
sum += (i * i);
else :
sum -= (i * i);
return sum;
if __name__ == "__main__" :
N = 2;
print(summation(N));
|
C#
using System;
class GFG
{
static int summation(int n)
{
int sum = 0;
for (int i = 1; i <= n; i++) {
if (i % 2 == 1)
sum += (i * i);
else
sum -= (i * i);
}
return sum;
}
public static void Main()
{
int N = 2;
Console.WriteLine(summation(N));
}
}
|
Javascript
<script>
function summation(n)
{
let sum = 0;
for (let i = 1; i <= n; i++) {
if (i % 2 == 1)
sum += (i * i);
else
sum -= (i * i);
}
return sum;
}
let N = 2;
document.write(summation(N));
</script>
|
Efficient Approach: O(1)
There exists a formula for finding the sum of squares of first n numbers with alternating signs:
![Rendered by QuickLaTeX.com \[\LARGE 1^{2}-2^{2}+3^{2}-4^{2}+... = (-1)^{n+1} \text{ } \frac{n(n+1)}{2}\]](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-c1cb79f89bcaa66b20929ec8fd6c4131_l3.png)
How does this work?
We can prove this formula using induction.
We can easily see that the formula is true for
n = 1 and n = 2 as sums are 1 and -3 respectively.
Let it be true for n = k-1. So sum of k-1 numbers
is (-1)k(k - 1) * k / 2
In the following steps, we show that it is true
for k assuming that it is true for k-1.
Sum of k numbers
=(-1)k (Sum of k-1 numbers + k2)
=(-1)k+1 ((k - 1) * k / 2 + k2)
=(-1)k+1 (k * (k + 1) / 2), which is true.
Hence inorder to find the sum of alternating sign squares of first N natural numbers, simply compute the formula 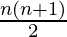 and print the result.
and print the result.
C++
#include <iostream>
using namespace std;
int summation(int n)
{
int abs_sum = n * (n + 1) / 2;
int sign = n + 1 % 2 == 0 ? 1 : -1;
int result_sum = sign * abs_sum;
return result_sum;
}
int main()
{
int N = 2;
cout << summation(N);
return 0;
}
|
Java
class GFG
{
static int summation(int n)
{
int abs_sum = n * (n + 1) / 2;
int sign = n + 1 % 2 == 0 ? 1 : -1;
int result_sum = sign * abs_sum;
return result_sum;
}
public static void main (String[] args)
{
int N = 2;
System.out.println(summation(N));
}
}
|
Python3
def summation(n) :
abs_sum = n * (n + 1) // 2;
sign = 1 if ((n + 1) % 2 == 0 ) else -1;
result_sum = sign * abs_sum;
return result_sum;
if __name__ == "__main__" :
N = 2;
print(summation(N));
|
C#
using System;
public class GFG
{
static int summation(int n)
{
int abs_sum = (int)(n * (n + 1) / 2);
int sign = n + 1 % 2 == 0 ? 1 : -1;
int result_sum = sign * abs_sum;
return result_sum;
}
public static void Main()
{
int N = 2;
Console.WriteLine(summation(N));
}
}
|
Javascript
<script>
function summation(n)
{
var abs_sum = n * (n + 1) / 2;
var sign = n + 1 % 2 == 0 ? 1 : -1;
var result_sum = sign * abs_sum;
return result_sum;
}
var N = 2;
document.write(summation(N));
</script>
|
Share your thoughts in the comments
Please Login to comment...