Python Program for Sum of squares of first n natural numbers

Given a positive integer N. The task is to find 1² + 2² + 3² + ….. + N². 

Examples:

Input : N = 4
Output : 30
12 + 22 + 32 + 42
= 1 + 4 + 9 + 16
= 30

Input : N = 5
Output : 55

Method 1: O(N) The idea is to run a loop from 1 to n and for each i, 1 <= i <= n, find i² to sum. 

python3

# Python3 Program to
# find sum of square
# of first n natural
# numbers


# Return the sum of
# square of first n
# natural numbers

def squaresum(n):

    # Iterate i from 1
    # and n finding
    # square of i and
    # add to sum.
    sm = 0
    for i in range(1, n+1):
        sm = sm + (i * i)

    return sm


# Driven Program
n = 4
print(squaresum(n))

# This code is contributed by Nikita Tiwari.*/

Output

30

Method 2: O(1)

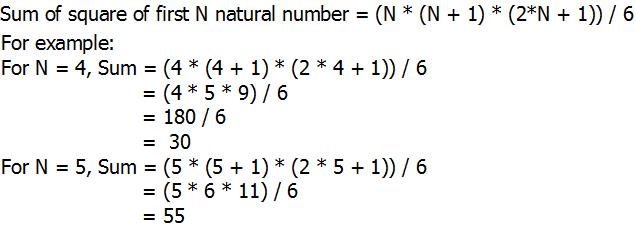
Proof:

We know,
(k + 1)3 = k3 + 3 * k2 + 3 * k + 1
We can write the above identity for k from 1 to n:
23 = 13 + 3 * 12 + 3 * 1 + 1 ......... (1)
33 = 23 + 3 * 22 + 3 * 2 + 1 ......... (2)
43 = 33 + 3 * 32 + 3 * 3 + 1 ......... (3)
53 = 43 + 3 * 42 + 3 * 4 + 1 ......... (4)
...
n3 = (n - 1)3 + 3 * (n - 1)2 + 3 * (n - 1) + 1 ......... (n - 1)
(n + 1)3 = n3 + 3 * n2 + 3 * n + 1 ......... (n)

Putting equation (n - 1) in equation n,
(n + 1)3 = (n - 1)3 + 3 * (n - 1)2 + 3 * (n - 1) + 1 + 3 * n2 + 3 * n + 1
         = (n - 1)3 + 3 * (n2 + (n - 1)2) + 3 * ( n + (n - 1) ) + 1 + 1

By putting all equation, we get
(n + 1)3 = 13 + 3 * Σ k2 + 3 * Σ k + Σ 1
n3 + 3 * n2 + 3 * n + 1 = 1 + 3 * Σ k2 + 3 * (n * (n + 1))/2 + n
n3 + 3 * n2 + 3 * n = 3 * Σ k2 + 3 * (n * (n + 1))/2 + n
n3 + 3 * n2 + 2 * n - 3 * (n * (n + 1))/2 = 3 * Σ k2
n * (n2 + 3 * n + 2) - 3 * (n * (n + 1))/2 = 3 * Σ k2
n * (n + 1) * (n + 2) - 3 * (n * (n + 1))/2 = 3 * Σ k2
n * (n + 1) * (n + 2 - 3/2) = 3 * Σ k2
n * (n + 1) * (2 * n + 1)/2  = 3 * Σ k2
n * (n + 1) * (2 * n + 1)/6  = Σ k2

python3

# Python3 Program to
# find sum of square
# of first n natural
# numbers

# Return the sum of
# square of first n
# natural numbers


def squaresum(n):
    return (n * (n + 1) * (2 * n + 1)) // 6


# Driven Program
n = 4
print(squaresum(n))

# This code is contributed by Nikita Tiwari.

Output

30

Time complexity: O(1)
Auxiliary space: O(1)

Avoiding early overflow: For large n, the value of (n * (n + 1) * (2 * n + 1)) would overflow. We can avoid overflow up to some extent using the fact that n*(n+1) must be divisible by 2. 

Python3

# Python Program to find sum of square of first
# n natural numbers. This program avoids
# overflow upto some extent for large value
# of n.y


def squaresum(n):
    return (n * (n + 1) / 2) * (2 * n + 1) / 3


# main()
n = 4
print(squaresum(n))

# Code Contributed by Mohit Gupta_OMG <(0_o)>

Output

30.0

Time complexity: O(1) because constant operations are being performed
Auxiliary space: O(1)

Approach: list comprehension

1. Take input from the user as a positive integer N using the input() function.
2. Convert the input string to an integer using the int() function and store it in a variable N.
3. Use a list comprehension to create a list of squares of numbers from 1 to N. The list comprehension should look like this: [i*i for i in range(1, N+1)]. This creates a list of squares of numbers from 1 to N.
4. Use the sum() function to find the sum of all elements in the list. Store the result in a variable sum_of_squares.
5. Print the result using the print() function. 

Python3

# Take input from user
N = 5

# Use list comprehension to create list of squares
squares_list = [i*i for i in range(1, N+1)]

# Find sum of squares using sum() function
sum_of_squares = sum(squares_list)

# Print the result
print("Sum of squares of first", N, "natural numbers is", sum_of_squares)

Output

Sum of squares of first 5 natural numbers is 55

The time complexity using a list comprehension is O(n)

The auxiliary space or space complexity is also O(n)

Approach: iterative 

We can use a loop to iterate through the first n natural numbers and calculate the sum of their squares.

Steps:

1. Initialize a variable sum to 0.
2. Use a loop to iterate through the first n natural numbers, i.e., from 1 to n.
3. Within the loop, calculate the square of the current number and add it to the sum.
4. After the loop completes, print the value of sum.

Python3

n = 4
sum = 0
for i in range(1, n+1):
    sum += i**2

print("The sum of squares of first", n, "natural numbers is", sum)

Output

The sum of squares of first 4 natural numbers is 30

Time Complexity: O(n)
Auxiliary Space: O(1)

Please refer complete article on Sum of squares of first n natural numbers for more details!

METHOD 5:Using recursion 

APPROACH:

This program calculates the sum of squares of first n natural numbers recursively.

ALGORITHM:

1.Define a function sum_of_squares(n) which takes an integer n as input.
2.Check if n is 1, return 1.
3.Else, calculate the sum of squares recursively by adding n*n with the sum_of_squares of n-1.
4.Set the value of N as 4.
5.Call sum_of_squares function with N as input and store the result in sum_of_squares variable.
6.Print the result.

Python3

def sum_of_squares(n):
    if n == 1:
        return 1
    else:
        return n*n + sum_of_squares(n-1)

N = 4
sum_of_squares = sum_of_squares(N)

print("Sum of squares of first", N, "natural numbers:", sum_of_squares)

Output

Sum of squares of first 4 natural numbers: 30

Time Complexity: O(n)
Space Complexity: O(n)