Sum of alternating sign cubes of first N Natural numbers
Last Updated :
05 Nov, 2021
Given a number N, the task is to find the sum of alternating sign cubes of first N natural numbers, i.e.,
13 – 23 + 33 – 43 + 53 – 63 + ….
Examples:
Input: N = 2
Output: -7
Explanation:
Required sum = 13 – 23 = -7
Input: N = 3
Output: 20
Explanation:
Required sum = 13 – 23 + 33 = 20
Naive Approach: A simple solution is to solve this problem by iterating over a loop from to N and compute the sum by alternating the sign each time.
Below is the implementation of above approach:
C++
#include <iostream>
using namespace std;
int summation(int n)
{
int sum = 0;
for (int i = 1; i <= n; i++)
if (i % 2 == 1)
sum += (i * i * i);
else
sum -= (i * i * i);
return sum;
}
int main()
{
int n = 3;
cout << summation(n);
return 0;
}
|
Java
import java.util.*;
class GFG {
static int summation(int n)
{
int sum = 0;
for(int i = 1; i <= n; i++)
{
if (i % 2 == 1)
sum += (i * i * i);
else
sum -= (i * i * i);
}
return sum;
}
public static void main(String[] args)
{
int n = 3;
System.out.println(summation(n));
}
}
|
Python3
def summation(n):
sum = 0
for i in range(1, n + 1):
if i % 2 == 1:
sum = sum + (i * i * i)
else:
sum = sum - (i * i * i)
return sum
n = 3
print(summation(n))
|
C#
using System;
class GFG{
static int summation(int n)
{
int sum = 0;
for(int i = 1; i <= n; i++)
{
if (i % 2 == 1)
sum += (i * i * i);
else
sum -= (i * i * i);
}
return sum;
}
public static void Main(String[] args)
{
int n = 3;
Console.WriteLine(summation(n));
}
}
|
Javascript
<script>
function summation(n)
{
let sum = 0;
for (let i = 1; i <= n; i++)
if (i % 2 == 1)
sum += (i * i * i);
else
sum -= (i * i * i);
return sum;
}
let n = 3;
document.write(summation(n));
</script>
|
Time Complexity: O(n)
Auxiliary Space: O(1)
Efficient Approach: The key observation in the problem is that every even number is with a negative sign, that is it used to reduce the overall sum. Therefore if we compute the sum of cubes of even numbers and odd numbers individually, then the overall sum can be computed easily.
- Count of Even or Odd numbers in first N natural numbers
=> 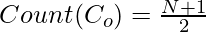
=> 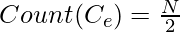
- Sum of first Even Terms
=> 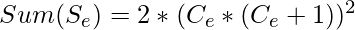
- Sum of first Odd Terms
=> 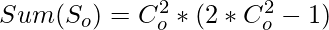
- Overall Sum
=> 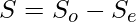
=> 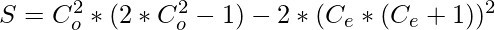
Below is the implementation of above approach:
C++
#include <bits/stdc++.h>
using namespace std;
int summation(int N)
{
int co = (N + 1) / 2;
int ce = (N) / 2;
int se = 2 * ((ce * (ce + 1))
* (ce * (ce + 1)));
int so = (co * co)
* (2 * ((co * co)) - 1);
return so - se;
}
int main()
{
int n = 3;
cout << summation(n);
return 0;
}
|
Java
import java.util.*;
class GFG{
static int summation(int N)
{
int co = (N + 1) / 2;
int ce = (N) / 2;
int se = 2 * ((ce * (ce + 1)) *
(ce * (ce + 1)));
int so = (co * co) * (2 * ((co * co)) - 1);
return so - se;
}
public static void main(String[] args)
{
int n = 3;
System.out.println(summation(n));
}
}
|
Python3
def summation(N):
co = (N + 1) / 2
co = int(co)
ce = N / 2
ce = int(ce)
se = 2 * ((ce * (ce + 1)) *
(ce * (ce + 1)))
so = (co * co) * (2 * (co * co) - 1)
return so - se
n = 3
print(summation(n))
|
C#
using System;
class GFG{
static int summation(int N)
{
int co = (N + 1) / 2;
int ce = (N) / 2;
int se = 2 * ((ce * (ce + 1)) *
(ce * (ce + 1)));
int so = (co * co) * (2 * ((co * co)) - 1);
return so - se;
}
public static void Main(String[] args)
{
int n = 3;
Console.WriteLine(summation(n));
}
}
|
Javascript
<script>
function summation(N)
{
var co = parseInt((N + 1) / 2);
var ce = parseInt((N) / 2);
var se = 2 * ((ce * (ce + 1)) *
(ce * (ce + 1)));
var so = (co * co) * (2 * ((co * co)) - 1);
return so - se;
}
var n = 3;
document.write(summation(n));
</script>
|
Time Complexity: O(1)
Auxiliary Space: O(1)
Like Article
Suggest improvement
Share your thoughts in the comments
Please Login to comment...