Successor Graph
Last Updated :
02 Nov, 2023
A Successor Graph is a directed graph in which each vertex has outdegree one, i.e., exactly one edge starts at each node. A successor graph consists of one or more components, each of which contains one cycle and some paths that lead to it.
Successor graphs are sometimes called functional graphs. The reason for this is that any successor graph corresponds to a function that defines the edges of the graph. The parameter for the function is a node of the graph, and the function gives the successor of that node. For Example, the function
The above function defines the below graph:
 Since each node of a successor graph has a unique successor, a function succ(x, k) can also be defined that gives the node when a traversal begin at node x and walk k steps forward. For example, in the above graph succ(4, 6) = 2, because node 2 can be reached by walking 6 steps from node 4:
Since each node of a successor graph has a unique successor, a function succ(x, k) can also be defined that gives the node when a traversal begin at node x and walk k steps forward. For example, in the above graph succ(4, 6) = 2, because node 2 can be reached by walking 6 steps from node 4: 
A straightforward way to calculate a value of succ(x, k) is to start at node x and walk k steps forward, which takes O(k) time. However, using preprocessing, any value of succ(x, k) can be calculated in only O(logk) time.
The idea is to precalculate all values of succ(x, k) where k is a power of two and at most u, where u is the maximum number of steps we will ever walk. This can be efficiently done because we can use the following recursion:
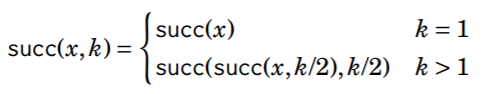
Precalculating the values takes O(n*log u) time because O(log u) values are calculated for each node. In the above graph, the first values are as follows:
|
| 3 | 5 | 7 | 6 | 2 | 2 | 1 | 6 | 3 |
| 7 | 2 | 1 | 2 | 5 | 5 | 3 | 2 | 7 |
| 3 | 2 | 7 | 2 | 5 | 5 | 1 | 2 | 3 |
| 7 | 2 | 1 | 2 | 5 | 5 | 3 | 2 | 7 |
| | | | | | | | | |
After this, any value of succ(x, k) can be calculated by presenting the number of steps k as a sum of powers of two.
For example, if we want to calculate the value of succ(x, 11), we first form the representation 11 = 8 + 2 + 1. Using that
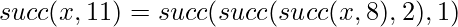
For example, in the previous graph
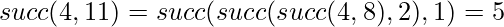
Such a representation always consists of O(log k) parts, so calculating a value of succ(x, k) takes O(log k) time.
Brute force
A straightforward way to calculate a value of succ(x, k) is to start at node x and walk k steps forward, which takes O(k) time.
/* Function to find the Kth successor of node x */
function succ(x, k, successor)
// repeat k times, change x -> successor(x)
for i from 1 to k
x = successor(x)
return x
Time Complexity:
O(K) per query, where ‘K’ is the number of successors we are interested in.
Space Complexity:
O(1), since we are not using any additional space to find the kth successor of a node.
Share your thoughts in the comments
Please Login to comment...