Sqrt (or Square Root) Decomposition | Set 2 (LCA of Tree in O(sqrt(height)) time)
Last Updated :
06 Apr, 2023
Prerequisite: Introduction and DFS
The task is to find LCA of two given nodes in a tree (not necessarily a Binary Tree). In previous posts, we have seen how to calculate LCA using the Sparse Matrix DP approach. In this post, we will see an optimization done on the Naive method by sqrt decomposition technique that works well over the Naive Approach.
Naive Approach
To calculate the LCA of two nodes first we will bring both the nodes to the same height by making the node with greater depth jump one parent up the tree till both the nodes are at the same height. Once, both the nodes are at the same height we can then start jumping one parent up for both the nodes simultaneously till both the nodes become equal and that node will be the LCA of the two originally given nodes.
Consider the below n-ary Tree with depth 9 and let’s examine how the naive approach works for this sample tree.
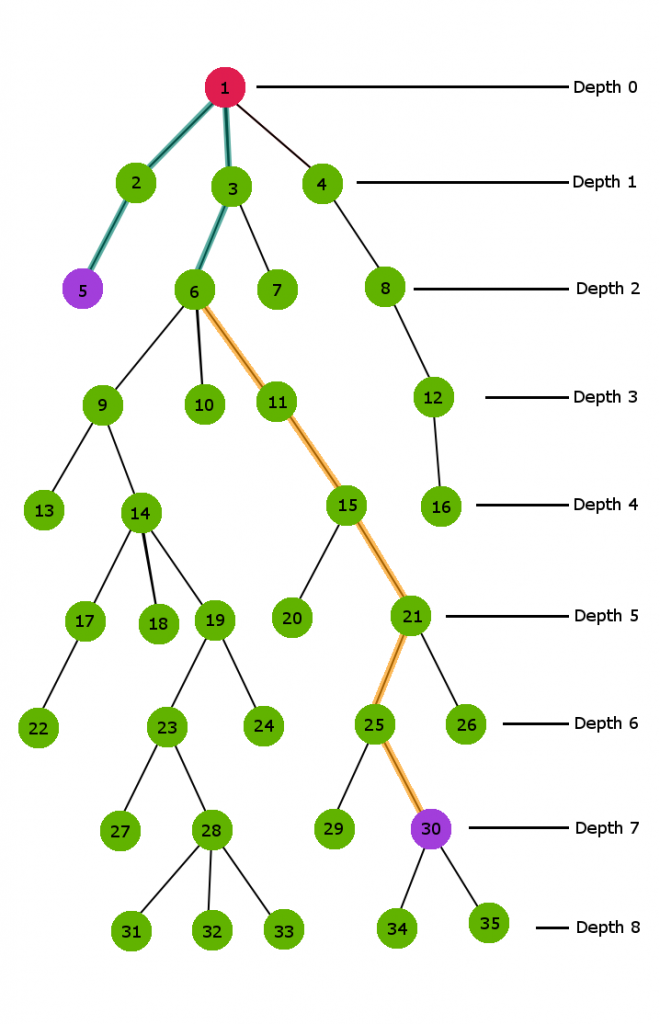
Here in the above Tree we need to calculate the LCA of node 6 and node 30
Clearly, node 30 has greater depth than node 6. So first of all we start jumping one parent above for node 30 till we reach the depth value of node 6 i.e at depth 2.
The orange colored path in the above figure demonstrates the jumping sequence to reach depth 2. In this procedure, we just simply jump one parent above the current node.
Now both nodes are at the same depth 2.Therefore, now both the nodes will jump one parent up till both the nodes become equal. This end node at which both the nodes become equal for the first time is our LCA.
The blue color path in the above figure shows the jumping route for both the nodes
Implementation:
C++
#include<bits/stdc++.h>
using namespace std;
#define MAXN 1001
int depth[MAXN];
int parent[MAXN];
vector < int > adj[MAXN];
void addEdge(int u,int v)
{
adj[u].push_back(v);
adj[v].push_back(u);
}
void dfs(int cur, int prev)
{
parent[cur] = prev;
depth[cur] = depth[prev] + 1;
for (int i=0; i<adj[cur].size(); i++)
if (adj[cur][i] != prev)
dfs(adj[cur][i],cur);
}
void preprocess()
{
depth[0] = -1;
dfs(1,0);
}
int LCANaive(int u,int v)
{
if (u == v) return u;
if (depth[u] > depth[v])
swap(u, v);
v = parent[v];
return LCANaive(u,v);
}
int main(int argc, char const *argv[])
{
addEdge(1,2);
addEdge(1,3);
addEdge(1,4);
addEdge(2,5);
addEdge(2,6);
addEdge(3,7);
addEdge(4,8);
addEdge(4,9);
addEdge(9,10);
addEdge(9,11);
addEdge(7,12);
addEdge(7,13);
preprocess();
cout << "LCA(11,8) : " << LCANaive(11,8) << endl;
cout << "LCA(3,13) : " << LCANaive(3,13) << endl;
return 0;
}
|
Java
import java.io.*;
import java.util.*;
class GFG
{
static int MAXN = 1001;
static int[] depth = new int[MAXN];
static int[] parent = new int[MAXN];
@SuppressWarnings("unchecked")
static Vector<Integer>[] adj = new Vector[MAXN];
static
{
for (int i = 0; i < MAXN; i++)
adj[i] = new Vector<>();
}
static void addEdge(int u, int v)
{
adj[u].add(v);
adj[v].add(u);
}
static void dfs(int cur, int prev)
{
parent[cur] = prev;
depth[cur] = depth[prev] + 1;
for (int i = 0; i < adj[cur].size(); i++)
if (adj[cur].elementAt(i) != prev)
dfs(adj[cur].elementAt(i), cur);
}
static void preprocess()
{
depth[0] = -1;
dfs(1, 0);
}
static int LCANaive(int u, int v)
{
if (u == v)
return u;
if (depth[u] > depth[v])
{
int temp = u;
u = v;
v = temp;
}
v = parent[v];
return LCANaive(u, v);
}
public static void main(String[] args)
{
addEdge(1, 2);
addEdge(1, 3);
addEdge(1, 4);
addEdge(2, 5);
addEdge(2, 6);
addEdge(3, 7);
addEdge(4, 8);
addEdge(4, 9);
addEdge(9, 10);
addEdge(9, 11);
addEdge(7, 12);
addEdge(7, 13);
preprocess();
System.out.println("LCA(11,8) : " + LCANaive(11, 8));
System.out.println("LCA(3,13) : " + LCANaive(3, 13));
}
}
|
Python3
MAXN = 1001
depth = [0 for i in range(MAXN)];
parent = [0 for i in range(MAXN)];
adj = [[] for i in range(MAXN)]
def addEdge(u, v):
adj[u].append(v);
adj[v].append(u);
def dfs(cur, prev):
parent[cur] = prev;
depth[cur] = depth[prev] + 1;
for i in range(len(adj[cur])):
if (adj[cur][i] != prev):
dfs(adj[cur][i], cur);
def preprocess():
depth[0] = -1;
dfs(1, 0);
def LCANaive(u, v):
if (u == v):
return u;
if (depth[u] > depth[v]):
u, v = v, u
v = parent[v];
return LCANaive(u, v);
if __name__ == "__main__":
addEdge(1, 2);
addEdge(1, 3);
addEdge(1, 4);
addEdge(2, 5);
addEdge(2, 6);
addEdge(3, 7);
addEdge(4, 8);
addEdge(4, 9);
addEdge(9, 10);
addEdge(9, 11);
addEdge(7, 12);
addEdge(7, 13);
preprocess();
print('LCA(11,8) : ' +
str(LCANaive(11, 8)))
print('LCA(3,13) : ' +
str(LCANaive(3, 13)))
|
C#
using System;
using System.Collections;
class GFG{
static int MAXN = 1001;
static int[] depth = new int[MAXN];
static int[] parent = new int[MAXN];
static ArrayList[] adj = new ArrayList[MAXN];
static void addEdge(int u, int v)
{
adj[u].Add(v);
adj[v].Add(u);
}
static void dfs(int cur, int prev)
{
parent[cur] = prev;
depth[cur] = depth[prev] + 1;
for(int i = 0; i < adj[cur].Count; i++)
if ((int)adj[cur][i] != prev)
dfs((int)adj[cur][i], cur);
}
static void preprocess()
{
depth[0] = -1;
dfs(1, 0);
}
static int LCANaive(int u, int v)
{
if (u == v)
return u;
if (depth[u] > depth[v])
{
int temp = u;
u = v;
v = temp;
}
v = parent[v];
return LCANaive(u, v);
}
public static void Main(string[] args)
{
for(int i = 0; i < MAXN; i++)
adj[i] = new ArrayList();
addEdge(1, 2);
addEdge(1, 3);
addEdge(1, 4);
addEdge(2, 5);
addEdge(2, 6);
addEdge(3, 7);
addEdge(4, 8);
addEdge(4, 9);
addEdge(9, 10);
addEdge(9, 11);
addEdge(7, 12);
addEdge(7, 13);
preprocess();
Console.WriteLine("LCA(11, 8) : " +
LCANaive(11, 8));
Console.WriteLine("LCA(3, 13) : " +
LCANaive(3, 13));
}
}
|
Javascript
<script>
var MAXN = 1001;
var depth = Array(MAXN);
var parent = Array(MAXN);
var adj = Array.from(Array(MAXN), ()=>Array());
function addEdge(u, v)
{
adj[u].push(v);
adj[v].push(u);
}
function dfs(cur, prev)
{
parent[cur] = prev;
depth[cur] = depth[prev] + 1;
for(var i = 0; i < adj[cur].length; i++)
if (adj[cur][i] != prev)
dfs(adj[cur][i], cur);
}
function preprocess()
{
depth[0] = -1;
dfs(1, 0);
}
function LCANaive(u, v)
{
if (u == v)
return u;
if (depth[u] > depth[v])
{
var temp = u;
u = v;
v = temp;
}
v = parent[v];
return LCANaive(u, v);
}
for(var i = 0; i < MAXN; i++)
adj[i] = [];
addEdge(1, 2);
addEdge(1, 3);
addEdge(1, 4);
addEdge(2, 5);
addEdge(2, 6);
addEdge(3, 7);
addEdge(4, 8);
addEdge(4, 9);
addEdge(9, 10);
addEdge(9, 11);
addEdge(7, 12);
addEdge(7, 13);
preprocess();
document.write("LCA(11, 8) : " +
LCANaive(11, 8)+"<br>");
document.write("LCA(3, 13) : " +
LCANaive(3, 13));
</script>
|
Output
LCA(11,8) : 4
LCA(3,13) : 3
Time Complexity: We pre-calculate the depth for each node using one DFS traversal in O(n). Now in the worst case, the two nodes will be two bottom-most nodes on the tree in different child branches of the root node. Therefore, in this case, the root will be the LCA of both the nodes. Hence, both the nodes will have to jump exactly h height above, where h is the height of the tree. So, to answer each LCA query Time Complexity will be O(h).
Auxiliary Space :O(MAXN)
The Sqrt Decomposition Trick :
We categorize nodes of the tree into different groups according to their depth. Assuming the depth of the tree h is a perfect square. So once again like the general sqrt decomposition approach, we will be having sqrt(h) blocks or groups. Nodes from depth 0 to depth sqrt(h) – 1 lie in the first group; then nodes having depth sqrt(H) to 2*sqrt(h)-1 lie in second group and so on till the last node.
We keep track of the corresponding group number for every node and also the depth of every node. This can be done by one single dfs on the tree (see the code for better understanding).
Sqrt trick :-
In the naive approach, we were jumping one parent up the tree till both nodes aren’t on the same depth. But here we perform the group-wise jump. To perform this group-wise jump, we need two-parameter associated with each node: 1) parent and 2) jump parent
Here parent for each node is defined as the first node above the current node that is directly connected to it, whereas jump_parent for each node is the node that is the first ancestor of the current node in the group just above the current node.
So, now we need to maintain 3 parameters for each node :
- depth
- parent
- jump_parent
All these three parameters can be maintained in one dfs(refer to the code for better understanding)
Pseudo code for the optimization process
LCAsqrt(u, v){
// assuming v is at greater depth
while (jump_parent[u]!=jump_parent[v]){
v = jump_parent[v];
}
// now both nodes are in same group
// and have same jump_parent
return LCAnaive(u,v);
}
The key concept here is that first we bring both the nodes in same group and having same jump_parent by climbing decomposed blocks above the tree one by one and then when both the nodes are in same group and have same jump_parent we use our naive approach to find LCA of the nodes.
This optimized group jumping technique reduces the iterating space by a factor of sqrt(h) and hence reduces the Time Complexity(refer below for better time complexity analysis)
Lets decompose the above tree in sqrt(h) groups (h = 9) and calculate LCA for node 6 and 30.
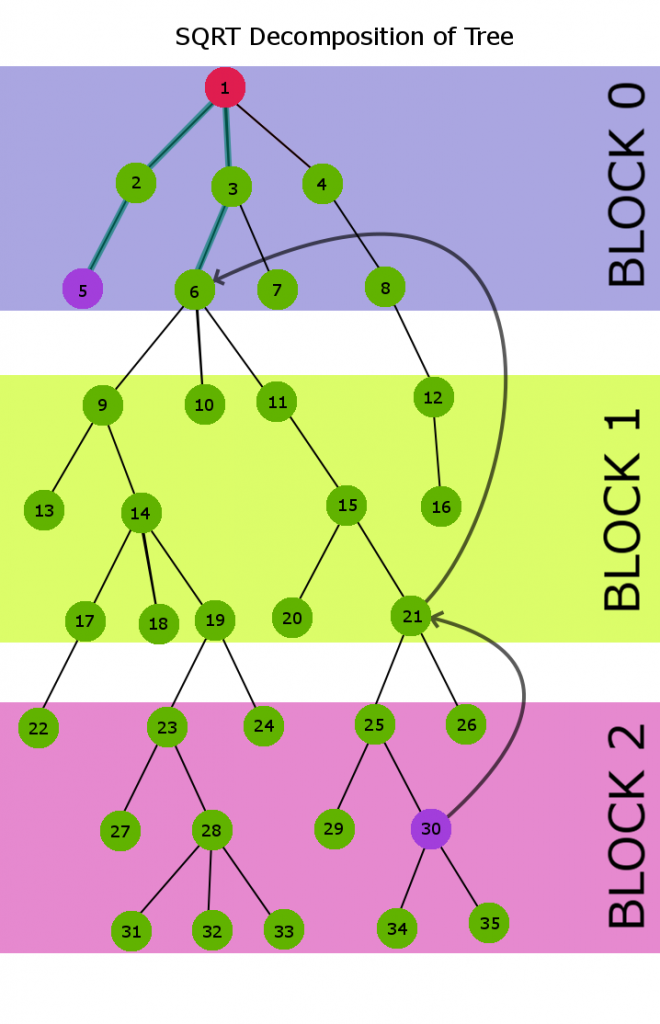
In the above decomposed tree
Jump_parent[6] = 0 parent[6] = 3
Jump_parent[5] = 0 parent[5] = 2
Jump_parent[1] = 0 parent[1] = 0
Jump_parent[11] = 6 parent[11] = 6
Jump_parent[15] = 6 parent[15] = 11
Jump_parent[21] = 6 parent[21] = 15
Jump_parent[25] = 21 parent[25] = 21
Jump_parent[26] = 21 parent[26] = 21
Jump_parent[30] = 21 parent[30] = 25
Now at this stage Jump_parent for node 30 is 21 and Jump_parent for node 5 is 0, So we will climp to jump_parent[30] i.e to node 21
Now once again Jump_parent of node 21 is not equal to Jump_parent of node 5, So once again we will climb to jump_parent[21] i.e node 6
At this stage jump_parent[6] == jump_parent[5], So now we will use our naive climbing approach and climb one parent above for both the nodes till it reach node 1 and that will be the required LCA .
Blue path in the above figure describes jumping path sequence for node 6 and node 5.
Implementation:
C++
#include "iostream"
#include "vector"
#include "math.h"
using namespace std;
#define MAXN 1001
int block_sz;
int depth[MAXN];
int parent[MAXN];
int jump_parent[MAXN];
vector < int > adj[MAXN];
void addEdge(int u,int v)
{
adj[u].push_back(v);
adj[v].push_back(u);
}
int LCANaive(int u,int v)
{
if (u == v) return u;
if (depth[u] > depth[v])
swap(u,v);
v = parent[v];
return LCANaive(u,v);
}
void dfs(int cur, int prev)
{
depth[cur] = depth[prev] + 1;
parent[cur] = prev;
if (depth[cur] % block_sz == 0)
jump_parent[cur] = parent[cur];
else
jump_parent[cur] = jump_parent[prev];
for (int i = 0; i<adj[cur].size(); ++i)
if (adj[cur][i] != prev)
dfs(adj[cur][i], cur);
}
int LCASQRT(int u, int v)
{
while (jump_parent[u] != jump_parent[v])
{
if (depth[u] > depth[v])
swap(u,v);
v = jump_parent[v];
}
return LCANaive(u,v);
}
void preprocess(int height)
{
block_sz = sqrt(height);
depth[0] = -1;
dfs(1, 0);
}
int main(int argc, char const *argv[])
{
addEdge(1,2);
addEdge(1,3);
addEdge(1,4);
addEdge(2,5);
addEdge(2,6);
addEdge(3,7);
addEdge(4,8);
addEdge(4,9);
addEdge(9,10);
addEdge(9,11);
addEdge(7,12);
addEdge(7,13);
int height = 4;
preprocess(height);
cout << "LCA(11,8) : " << LCASQRT(11,8) << endl;
cout << "LCA(3,13) : " << LCASQRT(3,13) << endl;
return 0;
}
|
Java
import java.util.*;
class GFG
{
static final int MAXN = 1001;
static int block_sz;
static int []depth = new int[MAXN];
static int []parent = new int[MAXN];
static int []jump_parent = new int[MAXN];
static Vector <Integer > []adj = new Vector[MAXN];
static void addEdge(int u,int v)
{
adj[u].add(v);
adj[v].add(u);
}
static int LCANaive(int u,int v)
{
if (u == v) return u;
if (depth[u] > depth[v])
{
int t = u;
u = v;
v = t;
}
v = parent[v];
return LCANaive(u, v);
}
static void dfs(int cur, int prev)
{
depth[cur] = depth[prev] + 1;
parent[cur] = prev;
if (depth[cur] % block_sz == 0)
jump_parent[cur] = parent[cur];
else
jump_parent[cur] = jump_parent[prev];
for (int i = 0; i < adj[cur].size(); ++i)
if (adj[cur].get(i) != prev)
dfs(adj[cur].get(i), cur);
}
static int LCASQRT(int u, int v)
{
while (jump_parent[u] != jump_parent[v])
{
if (depth[u] > depth[v])
{
int t = u;
u = v;
v = t;
}
v = jump_parent[v];
}
return LCANaive(u, v);
}
static void preprocess(int height)
{
block_sz = (int)Math.sqrt(height);
depth[0] = -1;
dfs(1, 0);
}
public static void main(String []args)
{
for (int i = 0; i < adj.length; i++)
adj[i] = new Vector<Integer>();
addEdge(1, 2);
addEdge(1, 3);
addEdge(1, 4);
addEdge(2, 5);
addEdge(2, 6);
addEdge(3, 7);
addEdge(4, 8);
addEdge(4, 9);
addEdge(9, 10);
addEdge(9, 11);
addEdge(7, 12);
addEdge(7, 13);
int height = 4;
preprocess(height);
System.out.print("LCA(11,8) : " + LCASQRT(11, 8) +"\n");
System.out.print("LCA(3,13) : " + LCASQRT(3, 13) +"\n");
}
}
|
Python3
import math
import collections
MAXN = 1001
block_sz = 0
depth = [0] * MAXN
parent = [0] * MAXN
jump_parent = [0] * MAXN
adj = collections.defaultdict(list)
def addEdge(u, v):
adj[u].append(v)
adj[v].append(u)
def LCANaive(u, v):
if u == v:
return u
if depth[u] > depth[v]:
u, v = v, u
v = parent[v]
return LCANaive(u, v)
def dfs(cur, prev):
depth[cur] = depth[prev] + 1
parent[cur] = prev
if depth[cur] % block_sz == 0:
jump_parent[cur] = parent[cur]
else:
jump_parent[cur] = jump_parent[prev]
for i in range(len(adj[cur])):
if adj[cur][i] != prev:
dfs(adj[cur][i], cur)
def LCASQRT(u, v):
while jump_parent[u] != jump_parent[v]:
if depth[u] > depth[v]:
u, v = v, u
v = jump_parent[v]
return LCANaive(u, v)
def preprocess(height):
global block_sz
block_sz = math.sqrt(height)
depth[0] = -1
dfs(1, 0)
if __name__ == "__main__":
addEdge(1, 2)
addEdge(1, 3)
addEdge(1, 4)
addEdge(2, 5)
addEdge(2, 6)
addEdge(3, 7)
addEdge(4, 8)
addEdge(4, 9)
addEdge(9, 10)
addEdge(9, 11)
addEdge(7, 12)
addEdge(7, 13)
height = 4
preprocess(height)
print("LCA(11,8) : ", LCASQRT(11, 8))
print("LCA(3,13) : ", LCASQRT(3, 13))
|
C#
using System;
using System.Collections.Generic;
public class GFG
{
static readonly int MAXN = 1001;
static int block_sz;
static int []depth = new int[MAXN];
static int []parent = new int[MAXN];
static int []jump_parent = new int[MAXN];
static List <int > []adj = new List<int>[MAXN];
static void addEdge(int u, int v)
{
adj[u].Add(v);
adj[v].Add(u);
}
static int LCANaive(int u, int v)
{
if (u == v) return u;
if (depth[u] > depth[v])
{
int t = u;
u = v;
v = t;
}
v = parent[v];
return LCANaive(u, v);
}
static void dfs(int cur, int prev)
{
depth[cur] = depth[prev] + 1;
parent[cur] = prev;
if (depth[cur] % block_sz == 0)
jump_parent[cur] = parent[cur];
else
jump_parent[cur] = jump_parent[prev];
for (int i = 0; i < adj[cur].Count; ++i)
if (adj[cur][i] != prev)
dfs(adj[cur][i], cur);
}
static int LCASQRT(int u, int v)
{
while (jump_parent[u] != jump_parent[v])
{
if (depth[u] > depth[v])
{
int t = u;
u = v;
v = t;
}
v = jump_parent[v];
}
return LCANaive(u, v);
}
static void preprocess(int height)
{
block_sz = (int)Math.Sqrt(height);
depth[0] = -1;
dfs(1, 0);
}
public static void Main(String []args)
{
for (int i = 0; i < adj.Length; i++)
adj[i] = new List<int>();
addEdge(1, 2);
addEdge(1, 3);
addEdge(1, 4);
addEdge(2, 5);
addEdge(2, 6);
addEdge(3, 7);
addEdge(4, 8);
addEdge(4, 9);
addEdge(9, 10);
addEdge(9, 11);
addEdge(7, 12);
addEdge(7, 13);
int height = 4;
preprocess(height);
Console.Write("LCA(11,8) : " + LCASQRT(11, 8) +"\n");
Console.Write("LCA(3,13) : " + LCASQRT(3, 13) +"\n");
}
}
|
Javascript
<script>
let MAXN = 1001;
let block_sz;
let depth = new Array(MAXN);
let parent = new Array(MAXN);
let jump_parent = new Array(MAXN);
let adj = new Array(MAXN);
function addEdge(u, v)
{
adj[u].push(v);
adj[v].push(u);
}
function LCANaive(u, v)
{
if (u == v)
return u;
if (depth[u] > depth[v])
{
let t = u;
u = v;
v = t;
}
v = parent[v];
return LCANaive(u, v);
}
function dfs(cur, prev)
{
depth[cur] = depth[prev] + 1;
parent[cur] = prev;
if (depth[cur] % block_sz == 0)
jump_parent[cur] = parent[cur];
else
jump_parent[cur] = jump_parent[prev];
for(let i = 0; i < adj[cur].length; ++i)
if (adj[cur][i] != prev)
dfs(adj[cur][i], cur);
}
function LCASQRT(u, v)
{
while (jump_parent[u] != jump_parent[v])
{
if (depth[u] > depth[v])
{
let t = u;
u = v;
v = t;
}
v = jump_parent[v];
}
return LCANaive(u, v);
}
function preprocess(height)
{
block_sz = parseInt(Math.sqrt(height), 10);
depth[0] = -1;
dfs(1, 0);
}
for(let i = 0; i < adj.length; i++)
adj[i] = [];
addEdge(1, 2);
addEdge(1, 3);
addEdge(1, 4);
addEdge(2, 5);
addEdge(2, 6);
addEdge(3, 7);
addEdge(4, 8);
addEdge(4, 9);
addEdge(9, 10);
addEdge(9, 11);
addEdge(7, 12);
addEdge(7, 13);
let height = 4;
preprocess(height);
document.write("LCA(11,8) : " +
LCASQRT(11, 8) + "</br>");
document.write("LCA(3,13) : " +
LCASQRT(3, 13) + "</br>");
</script>
|
Output
LCA(11,8) : 4
LCA(3,13) : 3
Note : The above code works even if height is not perfect square.
Now Lets see how the Time Complexity is changed by this simple grouping technique :
Time Complexity Analysis:
We have divided the tree into sqrt(h) groups according to their depth and each group contain nodes having max difference in their depth equal to sqrt(h). Now once again take an example of worst case, let’s say the first node ‘u’ is in first group and the node ‘v’ is in sqrt(h)th group(last group). So, first we will make group jumps(single group jumps) till we reach group 1 from last group; This will take exactly sqrt(h) – 1 iterations or jumps. So, till this step the Time Complexity is O(sqrt(h)).
Now once we are in same group, we call the LCAnaive function. The Time complexity for LCA_Naive is O(sqrt(h’)), where h’ is the height of the tree. Now, in our case value of h’ will be sqrt(h), because each group has a subtree of at max sqrt(h) height. So the complexity for this step is also O(sqrt(h)).
Hence, the total Time Complexity will be O(sqrt(h) + sqrt(h)) ~ O(sqrt(h)).
Share your thoughts in the comments
Please Login to comment...