Square Root (Sqrt) Decomposition Algorithm
Last Updated :
16 Aug, 2023
Square Root Decomposition Technique is one of the most common query optimization techniques used by competitive programmers. This technique helps us to reduce Time Complexity by a factor of sqrt(N)
The key concept of this technique is to decompose a given array into small chunks specifically of size sqrt(N)
Follow the below steps to solve the problem:
- We have an array of n elements and we decompose this array into small chunks of size sqrt(N)
- We will be having exactly sqrt(N) such chunks provided that N is a perfect square
- Therefore, now our array of N elements is decomposed into sqrt(N) blocks, where each block contains sqrt(N) elements (assuming the size of the array is a perfect square)
- Let’s consider these chunks or blocks as an individual array each of which contains sqrt(N) elements and you have computed your desired answer(according to your problem) individually for all the chunks
- Now, you need to answer certain queries asking you the answer for the elements in the range l to r(l and r are starting and ending indices of the array) in the original n-sized array
Naive Approach: To solve the problem follow the below idea:
Simply iterate over each element in the range l to r and calculate its corresponding answer. Therefore, the Time Complexity per query will be O(N)
Below is the code for above approach :
C++
#include <bits/stdc++.h>
using namespace std;
#define MAXN 10000
int arr[MAXN];
int query(int l, int r)
{
int sum = 0;
for (int i = l; i <= r; i++) {
sum += arr[i];
}
return sum;
}
int main()
{
int input[] = { 1, 5, 2, 4, 6, 1, 3, 5, 7, 10 };
int n = sizeof(input) / sizeof(input[0]);
memcpy(arr, input, sizeof(input));
cout << "query(3,8) : " << query(3, 8) << endl;
cout << "query(1,6) : " << query(1, 6) << endl;
arr[8] = 0;
cout << "query(8,8) : " << query(8, 8) << endl;
return 0;
}
|
Java
import java.util.Arrays;
public class GFG{
static int[] arr = new int[10000];
static int query(int l, int r) {
int sum = 0;
for (int i = l; i <= r; i++) {
sum += arr[i];
}
return sum;
}
public static void main(String[] args) {
int[] input = {1, 5, 2, 4, 6, 1, 3, 5, 7, 10};
int n = input.length;
System.arraycopy(input, 0, arr, 0, n);
System.out.println("query(3,8) : " + query(3, 8));
System.out.println("query(1,6) : " + query(1, 6));
arr[8] = 0;
System.out.println("query(8,8) : " + query(8, 8));
}
}
|
Python3
arr = [0] * 10000
def query(l, r):
_sum = 0
for i in range(l, r + 1):
_sum += arr[i]
return _sum
if __name__ == '__main__':
input_arr = [1, 5, 2, 4, 6, 1, 3, 5, 7, 10]
arr[:len(input_arr)] = input_arr
print("query(3,8) :", query(3, 8))
print("query(1,6) :", query(1, 6))
arr[8] = 0
print("query(8,8) :", query(8, 8))
|
C#
using System;
class Program
{
const int MAXN = 10000;
static int[] arr = new int[MAXN];
static int Query(int l, int r)
{
int sum = 0;
for (int i = l; i <= r; i++)
{
sum += arr[i];
}
return sum;
}
static void Main()
{
int[] input = { 1, 5, 2, 4, 6, 1, 3, 5, 7, 10 };
int n = input.Length;
Array.Copy(input, arr, n);
Console.WriteLine("query(3,8) : " + Query(3, 8));
Console.WriteLine("query(1,6) : " + Query(1, 6));
arr[8] = 0;
Console.WriteLine("query(8,8) : " + Query(8, 8));
}
}
|
Javascript
function query(l, r, arr) {
let sum = 0;
for (let i = l; i <= r; i++) {
sum += arr[i];
}
return sum;
}
const input = [1, 5, 2, 4, 6, 1, 3, 5, 7, 10];
const n = input.length;
const arr = [...input];
console.log("query(3,8) :", query(3, 8, arr));
console.log("query(1,6) :", query(1, 6, arr));
arr[8] = 0;
console.log("query(8,8) :", query(8, 8, arr));
|
Output
query(3,8) : 26
query(1,6) : 21
query(8,8) : 0
Efficient Approach(Sqrt Decomposition Trick): To solve the problem follow the below idea:
As we have already precomputed the answer for all individual chunks and now we need to answer the queries in range l to r. Now we can simply combine the answers of the chunks that lie in between the range l to r in the original array. So, if we see carefully here we are jumping sqrt(N) steps at a time instead of jumping 1 step at a time as done in the naive approach. Let’s just analyze its Time Complexity and implementation considering the below problem:
Problem :
Given an array of n elements. We need to answer q
queries telling the sum of elements in range l to
r in the array. Also the array is not static i.e
the values are changed via some point update query.
Range Sum Queries are of form : Q l r ,
where l is the starting index r is the ending index
Point update Query is of form : U idx val,
where idx is the index to update val is the
updated value
Below is the illustration of the above approach:
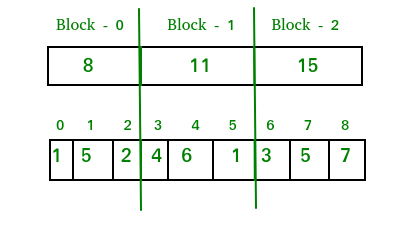
Let us consider that we have an array of 9 elements: A[] = {1, 5, 2, 4, 6, 1, 3, 5, 7}
1. Let’s decompose this array into sqrt(9) blocks, where each block will contain the sum of elements lying in it. Therefore now our decomposed array would look like this:
2. Till now we have constructed the decomposed array of sqrt(9) blocks and now we need to print the sum of elements in a given range.
So first let’s see two basic types of overlap that a range query can have on our array:
Range Query of type 1 (Given Range is on Block Boundaries) :

In this type the query, the range may totally cover the continuous sqrt blocks. So we can easily answer the sum of values in this range as the sum of completely overlapped blocks.
So the answer for the above query in the described image will be: ans = 11 + 15 = 26
Time Complexity: O(sqrt(N)). In the worst case, our range can be 0 to N-1(where N is the size of the array and assuming N to be a perfect square). In this case, all the blocks are completely overlapped by our query range. Therefore, to answer this query we need to iterate over all the decomposed blocks for the array and we know that the number of blocks = sqrt(N). Hence, the complexity for this type of query will be O(sqrt(N)) in the worst case.
Range Query of type 2 (Given Range is NOT on boundaries):
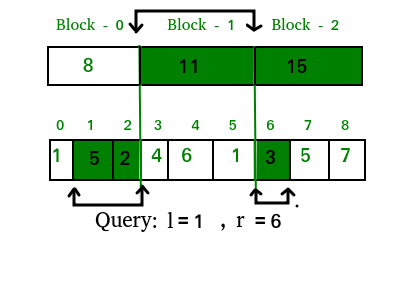
We can deal with these types of queries by summing the data from the completely overlapped decomposed blocks lying in the query range and then summing elements one by one from the original array whose corresponding block is not completely overlapped by the query range.
So the answer for the above query in the described image will be: ans = 5 + 2 + 11 + 3 = 21
Time Complexity: O(sqrt(N)). Let’s consider a query [l = 1 and r = n-2] (n is the size of the array and has 0-based indexing). Therefore, for this query exactly ( sqrt(n) – 2 ) blocks will be completely overlapped whereas the first and last blocks will be partially overlapped with just one element left outside the overlapping range. So, the completely overlapped blocks can be summed up in ( sqrt(n) – 2 ) ~ sqrt(n) iterations, whereas the first and last blocks are needed to be traversed one by one separately. But as we know that the number of elements in each block is at max sqrt(n), to sum up, the last block individually we need to make,
(sqrt(n)-1) ~ sqrt(n) iterations and same for the last block.
So, the overall Complexity = O(sqrt(n)) + O(sqrt(n)) + O(sqrt(n)) = O(3*sqrt(N)) = O(sqrt(N))
Update Queries(Point update):
In this query, we simply find the block in which the given index lies, then subtract its previous value and add the new updated value as per the point update query.
Time Complexity: O(1)
Below is the implementation of the above approach:
C++
#include <bits/stdc++.h>
using namespace std;
#define MAXN 10000
#define SQRSIZE 100
int arr[MAXN];
int block[SQRSIZE];
int blk_sz;
void update(int idx, int val)
{
int blockNumber = idx / blk_sz;
block[blockNumber] += val - arr[idx];
arr[idx] = val;
}
int query(int l, int r)
{
int sum = 0;
while (l < r and l % blk_sz != 0 and l != 0) {
sum += arr[l];
l++;
}
while (l + blk_sz - 1 <= r) {
sum += block[l / blk_sz];
l += blk_sz;
}
while (l <= r) {
sum += arr[l];
l++;
}
return sum;
}
void preprocess(int input[], int n)
{
int blk_idx = -1;
blk_sz = sqrt(n);
for (int i = 0; i < n; i++) {
arr[i] = input[i];
if (i % blk_sz == 0) {
blk_idx++;
}
block[blk_idx] += arr[i];
}
}
int main()
{
int input[] = { 1, 5, 2, 4, 6, 1, 3, 5, 7, 10 };
int n = sizeof(input) / sizeof(input[0]);
preprocess(input, n);
cout << "query(3,8) : " << query(3, 8) << endl;
cout << "query(1,6) : " << query(1, 6) << endl;
update(8, 0);
cout << "query(8,8) : " << query(8, 8) << endl;
return 0;
}
|
Java
import java.util.*;
class GFG {
static int MAXN = 10000;
static int SQRSIZE = 100;
static int[] arr = new int[MAXN];
static int[] block
= new int[SQRSIZE];
static int blk_sz;
static void update(int idx, int val)
{
int blockNumber = idx / blk_sz;
block[blockNumber] += val - arr[idx];
arr[idx] = val;
}
static int query(int l, int r)
{
int sum = 0;
while (l < r && l % blk_sz != 0 && l != 0) {
sum += arr[l];
l++;
}
while (l + blk_sz - 1 <= r) {
sum += block[l / blk_sz];
l += blk_sz;
}
while (l <= r) {
sum += arr[l];
l++;
}
return sum;
}
static void preprocess(int input[], int n)
{
int blk_idx = -1;
blk_sz = (int)Math.sqrt(n);
for (int i = 0; i < n; i++) {
arr[i] = input[i];
if (i % blk_sz == 0) {
blk_idx++;
}
block[blk_idx] += arr[i];
}
}
public static void main(String[] args)
{
int input[] = { 1, 5, 2, 4, 6, 1, 3, 5, 7, 10 };
int n = input.length;
preprocess(input, n);
System.out.println("query(3, 8) : " + query(3, 8));
System.out.println("query(1, 6) : " + query(1, 6));
update(8, 0);
System.out.println("query(8, 8) : " + query(8, 8));
}
}
|
Python 3
from math import sqrt
MAXN = 10000
SQRSIZE = 100
arr = [0]*(MAXN)
block = [0]*(SQRSIZE)
blk_sz = 0
def update(idx, val):
blockNumber = idx // blk_sz
block[blockNumber] += val - arr[idx]
arr[idx] = val
def query(l, r):
sum = 0
while (l < r and l % blk_sz != 0 and l != 0):
sum += arr[l]
l += 1
while (l + blk_sz - 1 <= r):
sum += block[l//blk_sz]
l += blk_sz
while (l <= r):
sum += arr[l]
l += 1
return sum
def preprocess(input, n):
blk_idx = -1
global blk_sz
blk_sz = int(sqrt(n))
for i in range(n):
arr[i] = input[i]
if (i % blk_sz == 0):
blk_idx += 1
block[blk_idx] += arr[i]
input = [1, 5, 2, 4, 6, 1, 3, 5, 7, 10]
n = len(input)
preprocess(input, n)
print("query(3,8) : ", query(3, 8))
print("query(1,6) : ", query(1, 6))
update(8, 0)
print("query(8,8) : ", query(8, 8))
|
C#
using System;
class GFG {
static int MAXN = 10000;
static int SQRSIZE = 100;
static int[] arr = new int[MAXN];
static int[] block
= new int[SQRSIZE];
static int blk_sz;
static void update(int idx, int val)
{
int blockNumber = idx / blk_sz;
block[blockNumber] += val - arr[idx];
arr[idx] = val;
}
static int query(int l, int r)
{
int sum = 0;
while (l < r && l % blk_sz != 0 && l != 0) {
sum += arr[l];
l++;
}
while (l + blk_sz - 1 <= r) {
sum += block[l / blk_sz];
l += blk_sz;
}
while (l <= r) {
sum += arr[l];
l++;
}
return sum;
}
static void preprocess(int[] input, int n)
{
int blk_idx = -1;
blk_sz = (int)Math.Sqrt(n);
for (int i = 0; i < n; i++) {
arr[i] = input[i];
if (i % blk_sz == 0) {
blk_idx++;
}
block[blk_idx] += arr[i];
}
}
public static void Main(String[] args)
{
int[] input = { 1, 5, 2, 4, 6, 1, 3, 5, 7, 10 };
int n = input.Length;
preprocess(input, n);
Console.WriteLine("query(3, 8) : " + query(3, 8));
Console.WriteLine("query(1, 6) : " + query(1, 6));
update(8, 0);
Console.WriteLine("query(8, 8) : " + query(8, 8));
}
}
|
Javascript
<script>
let MAXN = 10000;
let SQRSIZE = 100;
let arr = new Array(MAXN);
for(let i = 0; i < MAXN; i++)
{
arr[i] = 0;
}
let block = new Array(SQRSIZE);
for(let i = 0; i < SQRSIZE; i++)
{
block[i] = 0;
}
let blk_sz;
function update(idx,val)
{
let blockNumber = idx / blk_sz;
block[blockNumber] += val - arr[idx];
arr[idx] = val;
}
function query(l, r)
{
let sum = 0;
while (l < r && l % blk_sz != 0 && l != 0)
{
sum += arr[l];
l++;
}
while (l+blk_sz-1 <= r)
{
sum += block[l / blk_sz];
l += blk_sz;
}
while (l <= r)
{
sum += arr[l];
l++;
}
return sum;
}
function preprocess(input, n)
{
let blk_idx = -1;
blk_sz = Math.floor( Math.sqrt(n));
for (let i = 0; i < n; i++)
{
arr[i] = input[i];
if (i % blk_sz == 0)
{
blk_idx++;
}
block[blk_idx] += arr[i];
}
}
let input = [1, 5, 2, 4, 6, 1, 3, 5, 7, 10];
let n = input.length;
preprocess(input, n);
document.write("query(3, 8) : " +
query(3, 8)+"<br>");
document.write("query(1, 6) : " +
query(1, 6)+"<br>");
update(8, 0);
document.write("query(8, 8) : " +
query(8, 8)+"<br>");
</script>
|
Output
query(3,8) : 26
query(1,6) : 21
query(8,8) : 0
Time Complexity: O(N)
Auxiliary Space: O(MAXN), since MAXN extra space has been taken, where MAXN is the maximum value of N
Note: The above code works even if N is not a perfect square. In this case, the last block will contain even less number of elements than sqrt(N), thus reducing the number of iterations.
Let’s say n = 10. In this case, we will have 4 blocks first three blocks of size 3, and the last block of size 1.
Share your thoughts in the comments
Please Login to comment...