Regularity condition in the master theorem.
Last Updated :
06 Oct, 2017
Master theorem is a direct way to get the solution of a recurrence relation, provided that it is of the following type:
T(n) = aT(n/b) + f(n) where a >= 1 and b > 1
The theorem consists of the following three cases:
1.If f(n) =
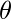
(
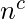
) where c <
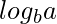
then T(n) =
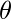
(n
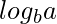
)
2.If f(n) =
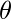
(
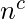
) where c =
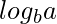
then T(n) =
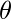
(
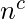
Log n)
3.If f(n) =
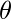
(
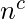
) where c >
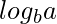
then T(n) =
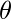
(f(n))
Imagine the recurrence
aT(n/b) + f(n) in the form of a tree.
Case 1 covers the case when the children nodes does more work than the parent node.
For example the equation
T(n)=2T(n/2)+1 falls under the category of case 1 and we can clearly see from it’s tree below that at each level the children nodes perform twice as much work as the parent node.
T(n) ------(1)
/ \
T(n/2) T(n/2) ------(2)
/ \ / \
Case 2 covers the case when the children node and the parent node does an equal amount of work.
For example the equation
T(n)=2T(n/2)+n falls under the category of case 2 and we can clearly see from it’s tree below that at each level the children nodes perform as much work as the parent node.
T(n) ------(n)
/ \
T(n/2) T(n/2) ------(n)
/ \ / \
Case 3 covers the scenario that the parent node does more work than the children nodes.
T(n)=T(n/2)+n is a example of case 3 where the parent performs more work than the child.
T(n) ------(n)
|
T(n/2) ------(n/2)
|
In case 1 and case 2 the case conditions themselves make sure that work done by children is either more or equal to the parent but that is not the case with case 3.
In case 3 we apply a
regulatory condition to make sure that the parent does at least as much as the children.
The regulatory condition for case 3 is
af(n/b)<=cf(n).
This says that f(n) (the amount of work done in the root) needs to be at least as big as the sum of the work done in the lower levels.
The equation
T(n) = T(n/2) + n(sin(n – 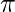 /2) + 2)
/2) + 2) is a example where regulatory condition makes a huge difference. The equation isn’t satisfying case 1 and case 2. In case 3 for large values of n it can never satisfy the regulatory condition. Hence this equation is beyond the scope of master theorem.
Share your thoughts in the comments
Please Login to comment...