Hypothesis (language regularity) and algorithm (L-graph to NFA) in TOC
Last Updated :
19 May, 2023
Prerequisite – Finite automata, L-graphs and what they represent L-graphs can generate context sensitive languages, but it’s much harder to program a context sensitive language over programming a regular one. This is why I’ve came up with a hypothesis about what kind of L-graphs can generate a regular language. But first, I need to introduce you to what I call an iterating nest. As you can remember a nest is a neutral path 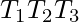 , where
, where 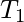 and
and 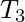 are cycles and
are cycles and 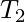 path is neutral. We will call
path is neutral. We will call 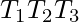 an iterating nest, if
an iterating nest, if 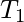 ,
, 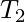 and
and 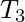 paths print the same string of symbols several times, to be more exact
paths print the same string of symbols several times, to be more exact 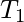 prints
prints  ,
, 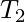 prints
prints 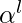 ,
, 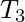 prints
prints 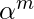 ,
,  and
and  is a string of input symbols (better, if at least one of
is a string of input symbols (better, if at least one of  ). From this definition comes out the next hypothesis. Hypothesis – If in a context free L-graph G all nests are iterating, then the language defined by this L-graph G, L(G), is regular. If this hypothesis will be proven in the near future, it can change a lot in programming that will make creating new easy programming languages much easier than it already is. The hypothesis above leads to the next algorithm of converting context free L-graphs with iterating nests to an NFA. Algorithm – Converting a context free L-graph with iterating complements to a corresponding NFA Input – Context free L-graph
). From this definition comes out the next hypothesis. Hypothesis – If in a context free L-graph G all nests are iterating, then the language defined by this L-graph G, L(G), is regular. If this hypothesis will be proven in the near future, it can change a lot in programming that will make creating new easy programming languages much easier than it already is. The hypothesis above leads to the next algorithm of converting context free L-graphs with iterating nests to an NFA. Algorithm – Converting a context free L-graph with iterating complements to a corresponding NFA Input – Context free L-graph  with iterating complements Output –
with iterating complements Output – 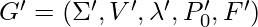
- Step-1: Languages of the L-graph and NFA must be the same, thusly, we won’t need a new alphabet
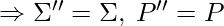 . (Comment: we build context free L-graph G’’, which is equal to the start graph G’, with no conflicting nests)
. (Comment: we build context free L-graph G’’, which is equal to the start graph G’, with no conflicting nests) - Step-2: Build Core(1, 1) for the graph G. V’’ := {(v,
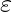 ) | v
) | v 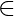 V of
V of 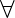 canon k
canon k 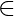 Core(1, 1), v
Core(1, 1), v 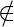 k}
k} 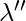 := { arcs
:= { arcs 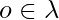 | start and final states
| start and final states  V’’} For all k
V’’} For all k 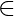 Core(1, 1): Step 1’. v := 1st state of canon k.
Core(1, 1): Step 1’. v := 1st state of canon k. 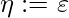 . V’’
. V’’ 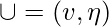 Step 2’.
Step 2’. 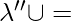 arc from state
arc from state 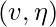 followed this arc into new state defined with following rules:
followed this arc into new state defined with following rules: 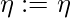 , if the input bracket on this arc
, if the input bracket on this arc 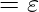 ;
; 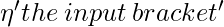 , if the input bracket is an opening one;
, if the input bracket is an opening one; 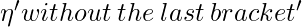 , if the input bracket is a closing bracket v := 2nd state of canon k V’’
, if the input bracket is a closing bracket v := 2nd state of canon k V’’  Step 3’. Repeat Step 2’, while there are still arcs in the canon.
Step 3’. Repeat Step 2’, while there are still arcs in the canon. - Step-3: Build Core(1, 2). If the canon has 2 equal arcs in a row: the start state and the final state match; we add the arc from given state into itself, using this arc, to
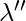 . Add the remaining in
. Add the remaining in 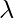 arcs v – u
arcs v – u  to
to 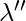 in the form of
in the form of 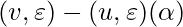
- Step-4:
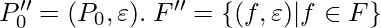 (Comment: following is an algorithm of converting context free L-graph G’’ into NFA G’)
(Comment: following is an algorithm of converting context free L-graph G’’ into NFA G’) - Step-5: Do the following to every iterating complement
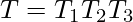 in G’’: Add a new state v. Create a path that starts in state
in G’’: Add a new state v. Create a path that starts in state 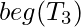 , equal to
, equal to 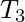 . From v into
. From v into 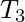 create the path, equal to
create the path, equal to 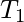 . Delete cycles
. Delete cycles 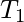 and
and 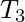 .
. - Step-6: G’ = G’’, where arcs are not loaded with brackets.
So that every step above is clear I’m showing you the next example.  Context free L-graph with iterating complements
Context free L-graph with iterating complements ![Rendered by QuickLaTeX.com G = ( \{a, b, c\}, \\*\{1, 2, 3\} \\*\{( (, ) ), ( [, ] )\}, \\*\\*\{ (: \{ 1 - a - 1 \}, \\*): \{ 2 - a - 2 \}, \\*\big[: \{ 1 - b - 2 \}, \\*\big]: \{ 2 - c - 3 \}, \\*\varepsilon: \{ 1 - a - 2 \} \}, \\*\\*1, \\*\{2, 3\} \}](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-50f4fb3d3a3d1fa6f725e84c494e1354_l3.png) , which determines the
, which determines the 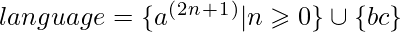
 Start graph G
Start graph G  Core(1, 1) = { 1 – a – 2 ; 1 – a, (1 – 1 – a – 2 – a, )1 – 2 ; 1 – b, (2 – 2 – c, )2 – 3 } Core(1, 2) = Core(1, 1)
Core(1, 1) = { 1 – a – 2 ; 1 – a, (1 – 1 – a – 2 – a, )1 – 2 ; 1 – b, (2 – 2 – c, )2 – 3 } Core(1, 2) = Core(1, 1)  { 1 – a, (1 – 1 – a, (1 – 1 – a – 2 – a, )1 – 2 – a, )1 – 2 } Step 2: Step 1’ – Step 3’
{ 1 – a, (1 – 1 – a, (1 – 1 – a – 2 – a, )1 – 2 – a, )1 – 2 } Step 2: Step 1’ – Step 3’ ![Rendered by QuickLaTeX.com \Rightarrow\\ V'' = \{(1, \varepsilon), (2, (_2), (3, \varepsilon), (1, (_1), (2, )_1), (2, \varepsilon)\}\\* \lambda'' = \{ \\*(: \{ (1, \varepsilon) - a - (1, (); (1, () - a - (1, () \}, \\*): \{ (2, )) - a - (2, )); (2, )) - a - (2, \varepsilon) \}, \\*\big[: \{ (1, \varepsilon) - b - (2, [) \}, \\*\big]: \{ (2, [) - c - (3, \varepsilon) \}, \\*\varepsilon: \{ (1, \varepsilon) - a - (2, \varepsilon); (1, () - a - (2, )) \} \}\\ P''_0 = (1, \varepsilon)\\ F'' = \{(2, \varepsilon), (3, \varepsilon)\}\\ G'' = (\Sigma'', V'', P'', \lambda'', P''_0, F'')](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-51dd8f4b60c300a67e869a710476f71a_l3.png)
 Intermediate graph G’’
Intermediate graph G’’ 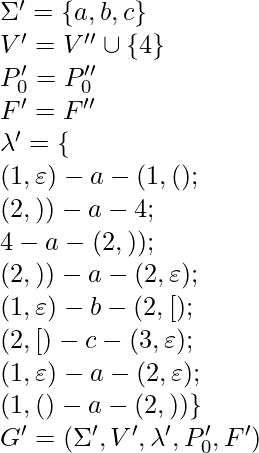
 NFA G’
NFA G’
Advantages of hypotheses (language regularity) in TOC:
Framework for analysis: Hypotheses about language regularity provide a structured framework for analyzing and classifying languages. By categorizing languages into different classes (e.g., regular, context-free, etc.), researchers can study the properties, limitations, and computational complexities associated with each class.
Understanding language behavior: Hypotheses about language regularity help in understanding the behavior of languages. Regular languages, for example, have well-defined properties and can be recognized by finite automata. By assuming the regularity of a language, researchers can employ known techniques and tools to analyze and process the language efficiently.
Bridging theory and practice: Hypotheses related to language regularity act as a bridge between theoretical foundations and practical applications. The study of regular languages allows for the development of algorithms and techniques that are widely applicable in areas such as compiler design, pattern matching, and text processing.
Disadvantages of hypotheses (language regularity) in TOC:
Limitations of classification: Hypotheses about language regularity rely on a classification system that may have inherent limitations. Not all languages fit neatly into predefined classes, and some languages may possess properties that fall outside traditional categorizations. This can make it challenging to accurately classify languages and determine their regularity.
Complex languages: Hypotheses about language regularity often focus on simpler languages, such as regular languages. However, real-world problems and applications may involve more complex languages, such as context-free or context-sensitive languages. In such cases, the regularity assumption may not hold, and alternative approaches or formalisms may be necessary.
Like Article
Suggest improvement
Share your thoughts in the comments
Please Login to comment...