Midy’s theorem
Last Updated :
24 Mar, 2023
According to Midy’s theorem, if the period of a repeating decimal for 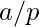 , where p is prime and
, where p is prime and 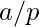 is a reduced fraction, has an even number of digits, then dividing the repeating portion into halves and adding gives a string of 9s.
is a reduced fraction, has an even number of digits, then dividing the repeating portion into halves and adding gives a string of 9s.
Examples :
a = 1 and p = 7
1/7 = 0.14285714285..
So 1/7 is a repeating decimal with 142857 being repeated. Now, according to the theorem, it has even number of repeating digits i.e. 142857. Further if we divide this into two halves, we get 142 and 857. Thus, on adding these two, we get 999 which is string of 9s and matches our theorem.
a = 2 and p = 11
2/11 = 0.18181818181..
Here, repeating decimal is 18. Now this is even in number therefore 1+8 = 9 which again shows the validity of Midy’s theorem.
Given numerator and denominator, the task is to find if the resultant floating point number follows Midy’s theorem or not.
Approach :
Let us simulate the process of converting fraction to decimal. Let us look at the part where we have already figured out the integer part which is floor(numerator/denominator). Now we are left with ( remainder = numerator%denominator ) / denominator.
If you remember the process of converting to decimal, at each step we do the following :
- Multiply the remainder by 10.
- Append remainder / denominator to result.
- Remainder = remainder % denominator.
At any moment, if remainder becomes 0, we are done.
However, when there is a recurring sequence, remainder never becomes 0. For example if you look at 1/3, the remainder never becomes 0.
Below is one important observation :
If we start with remainder ‘rem’ and if the remainder repeats at any point of time, the digits between the two occurrence of ‘rem’ keep repeating.
So the idea is to store seen remainders in a map. Whenever a remainder repeats, we return the sequence before the next occurrence.
Below is the implementation of Midy’s theorem :
C++
#include <bits/stdc++.h>
using namespace std;
string fractionToDecimal(int numerator, int denominator)
{
string res;
map<int, int> mp;
mp.clear();
int rem = numerator % denominator;
while ((rem != 0) && (mp.find(rem) == mp.end()))
{
mp[rem] = res.length();
rem = rem * 10;
int res_part = rem / denominator;
res += to_string(res_part);
rem = rem % denominator;
}
return (rem == 0) ? "-1" : res.substr(mp[rem]);
}
bool isPrime(int n)
{
for (int i = 2; i <= n / 2; i++)
if (n % i == 0)
return false;
return true;
}
void Midys(string str, int n)
{
int l = str.length();
int part1 = 0, part2 = 0;
if (!isPrime(n))
{
cout << "Denominator is not prime, "
<< "thus Midy's theorem is not applicable";
}
else if (l % 2 == 0)
{
for (int i = 0; i < l / 2; i++)
{
part1 = part1 * 10 + (str[i] - '0');
part2 = part2 * 10 + (str[l / 2 + i] - '0');
}
cout << part1 << " + " << part2 << " = "
<< (part1 + part2) << endl;
cout << "Midy's theorem holds!";
}
else
{
cout << "The repeating decimal is of odd length "
<< "thus Midy's theorem is not applicable";
}
}
int main()
{
int numr = 2, denr = 11;
string res = fractionToDecimal(numr, denr);
if (res == "-1")
cout << "The fraction does not have repeating decimal";
else {
cout << "Repeating decimal = " << res << endl;
Midys(res, denr);
}
return 0;
}
|
Java
import java.util.*;
class GFG{
static String fractionToDecimal(int numerator,
int denominator)
{
String res = "";
HashMap<Integer, Integer> mp = new HashMap<>();
int rem = numerator % denominator;
while ((rem != 0) && !mp.containsKey(rem))
{
mp.put(rem, res.length());
rem = rem * 10;
int res_part = rem / denominator;
res += res_part + "";
rem = rem % denominator;
}
return (rem == 0) ? "-1" : res.substring(mp.get(rem));
}
static boolean isPrime(int n)
{
for(int i = 2; i <= n / 2; i++)
if (n % i == 0)
return false;
return true;
}
static void Midys(String str, int n)
{
int l = str.length();
int part1 = 0, part2 = 0;
if (!isPrime(n))
{
System.out.print("Denominator is not prime, " +
"thus Midy's theorem is not " +
"applicable");
}
else if (l % 2 == 0)
{
for(int i = 0; i < l / 2; i++)
{
part1 = part1 * 10 + (str.charAt(i) - '0');
part2 = part2 * 10 + (str.charAt(l / 2 + i) - '0');
}
System.out.println(part1 + " + " + part2 +
" = " + (part1 + part2));
System.out.print("Midy's theorem holds!");
}
else
{
System.out.print("The repeating decimal is " +
"of odd length thus Midy's "+
"theorem is not applicable");
}
}
public static void main(String []args)
{
int numr = 2, denr = 11;
String res = fractionToDecimal(numr, denr);
if (res == "-1")
System.out.print("The fraction does not " +
"have repeating decimal");
else
{
System.out.println("Repeating decimal = " + res);
Midys(res, denr);
}
}
}
|
Python3
def fractionToDecimal(numerator, denominator):
res = ""
mp = dict()
rem = numerator % denominator
while ((rem != 0) and (rem not in mp)):
mp[rem] = len(res)
rem = rem * 10
res_part = (rem // denominator)
res += str(res_part)
rem = rem % denominator
return ["-1", res[mp[rem]:]][rem != 0]
def isPrime(n):
for i in range(2, 1 + n // 2):
if (n % i == 0):
return False
return True
def Midys(str, n):
l = len(str)
part1 = 0
part2 = 0
if (not isPrime(n)):
print("Denominator is not prime, thus Midy's theorem is not applicable")
elif (l % 2 == 0):
for i in range(l // 2):
part1 = part1 * 10 + int(str[i])
part2 = part2 * 10 + int(str[(l // 2) + i])
print(part1, "+", part2, "=", (part1 + part2))
print("Midy's theorem holds!")
else:
print(
"The repeating decimal is of odd length thus Midy's theorem is not applicable")
numr = 2
denr = 11
res = fractionToDecimal(numr, denr)
if (res == "-1"):
print("The fraction does not have repeating decimal")
else:
print("Repeating decimal =", res)
Midys(res, denr)
|
C#
using System;
using System.Collections;
using System.Collections.Generic;
class GFG{
static String fractionToDecimal(int numerator,
int denominator)
{
String res = "";
Dictionary<int,int> mp = new Dictionary<int,int>();
int rem = numerator % denominator;
while ((rem != 0) && !mp.ContainsKey(rem))
{
mp[rem]= res.Length;
rem = rem * 10;
int res_part = rem / denominator;
res += res_part + "";
rem = rem % denominator;
}
return (rem == 0) ? "-1" : res.Substring(mp[rem]);
}
static bool isPrime(int n)
{
for(int i = 2; i <= n / 2; i++)
if (n % i == 0)
return false;
return true;
}
static void Midys(String str, int n)
{
int l = str.Length;
int part1 = 0, part2 = 0;
if (!isPrime(n))
{
Console.Write("Denominator is not prime, " +
"thus Midy's theorem is not " +
"applicable");
}
else if (l % 2 == 0)
{
for(int i = 0; i < l / 2; i++)
{
part1 = part1 * 10 + (str[i] - '0');
part2 = part2 * 10 + (str[l / 2 + i] - '0');
}
Console.WriteLine(part1 + " + " + part2 +
" = " + (part1 + part2));
Console.Write("Midy's theorem holds!");
}
else
{
Console.Write("The repeating decimal is " +
"of odd length thus Midy's "+
"theorem is not applicable");
}
}
public static void Main(string []args)
{
int numr = 2, denr = 11;
string res = fractionToDecimal(numr, denr);
if (res == "-1")
Console.Write("The fraction does not " +
"have repeating decimal");
else
{
Console.WriteLine("Repeating decimal = " + res);
Midys(res, denr);
}
}
}
|
Javascript
function fractionToDecimal(numerator, denominator)
{
let res = "";
let mp = {};
let rem = numerator % denominator;
while ((rem != 0) && (!mp.hasOwnProperty(rem)))
{
mp[rem] = res.length;
rem = rem * 10;
let res_part = Math.floor(rem / denominator);
res += (res_part.toString());
rem = rem % denominator;
}
return (rem == 0) ? "-1" : res.substr(mp[rem]);
}
function isPrime(n)
{
for (var i = 2; i <= n / 2; i++)
if (n % i == 0)
return false;
return true;
}
function Midys(str, n)
{
var l = str.length;
var part1 = 0, part2 = 0;
if (!isPrime(n))
{
console.log("Denominator is not prime, thus Midy's theorem is not applicable");
}
else if (l % 2 == 0)
{
for (var i = 0; i < l / 2; i++)
{
part1 = part1 * 10 + parseInt(str[i]);
part2 = part2 * 10 + parseInt(str[(Math.floor(l / 2) + i)]);
}
console.log(part1 + " + " + part2 + " = " + (part1 + part2));
console.log("Midy's theorem holds!");
}
else
{
console.log("The repeating decimal is of odd length thus Midy's theorem is not applicable");
}
}
let numr = 2;
let denr = 11;
let res = fractionToDecimal(numr, denr);
if (res == "-1")
console.log("The fraction does not have repeating decimal");
else
{
console.log("Repeating decimal = " + res);
Midys(res, denr);
}
|
Output :
Repeating decimal = 18
1 + 8 = 9
Midy's theorem holds!
Time Complexity: O(n*log(n))
Auxiliary Space: O(n)
More about Midy’s theorem can be found on
http://www.kurims.kyoto-u.ac.jp/EMIS/journals/INTEGERS/papers/h2/h2.pdf
http://digitalcommons.unl.edu/cgi/viewcontent.cgi?article=1047&context=mathfacpub
Like Article
Suggest improvement
Share your thoughts in the comments
Please Login to comment...