Master Theorem For Subtract and Conquer Recurrences
Last Updated :
31 May, 2021
Master theorem is used to determine the Big – O upper bound on functions which possess recurrence, i.e which can be broken into sub problems.
Master Theorem For Subtract and Conquer Recurrences:
Let T(n) be a function defined on positive n as shown below:
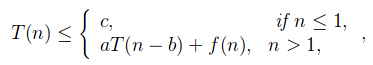
for some constants c, a>0, b>0, k>=0 and function f(n). If f(n) is O(nk), then
1. If a<1 then T(n) = O(nk)
2. If a=1 then T(n) = O(nk+1)
3. if a>1 then T(n) = O(nkan/b)
Proof of above theorem( By substitution method ):
From above function, we have:
T(n) = aT(n-b) + f(n)
T(n-b) = aT(n-2b) + f(n-b)
T(n-2b) = aT(n-3b) + f(n-2b)
Now,
T(n-b) = a2T(n-3b) + af(n-2b) + f(n-b)
T(n) = a3T(n-3b) + a2f(n-2b) + af(n-b) + f(n)
T(n) = ?i=0 to n ai f(n-ib) + constant, where f(n-ib) is O(n-ib)
T(n) = O(nk ?i=0 to n/b ai )
Where,
If a<1 then ?i=0 to n/b ai = O(1), T(n) = O(nk)
If a=1 then ?i=0 to n/b ai = O(n), T(n) = O(nk+1)
If a>1 then ?i=0 to n/b ai = O(an/b), T(n) = O(nkan/b)
Consider the following program for nth fibonacci number:
C++
#include<stdio.h>
int fib(int n)
{
if (n <= 1)
return n;
return fib(n-1) + fib(n-2);
}
int main ()
{
int n = 9;
printf("%d", fib(n));
getchar();
return 0;
}
|
Python3
def fib(n):
if (n <= 1):
return n
return fib(n - 1) + fib(n - 2)
n = 9
print(fib(n))
|
Java
class clg
{
static int fib(int n)
{
if (n <= 1)
return n;
return fib(n-1) + fib(n-2);
}
public static void main (String[] args)
{
int n = 9;
System.out.println( fib(n));
}
}
|
C#
using System;
class GFG
{
static int fib(int n)
{
if (n <= 1)
return n;
return fib(n - 1) + fib(n - 2);
}
public static void Main(String[] args)
{
int n = 9;
Console.WriteLine(fib(n));
}
}
|
PHP
<?php
function fib($n)
{
if ($n <= 1)
return $n;
return fib($n - 1) +
fib($n - 2);
}
$n = 9;
echo fib($n);
?>
|
Javascript
<script>
function fib(n)
{
if (n <= 1)
return n;
return fib(n - 1) + fib(n - 2);
}
let n = 9;
document.write(fib(n));
</script>
|
Output
34
Time complexity Analysis:
The recursive function can be defined as, T(n) = T(n-1) + T(n-2)
- For Worst Case, Let T(n-1) ? T(n-2)
T(n) = 2T(n-1) + c
where,f(n) = O(1)
? k=0, a=2, b=1;
T(n) = O(n02n/1)
= O(2n)
- For Best Case, Let T(n-2) ? T(n-1)
T(n) = 2T(n-2) + c
where,f(n) = O(1)
? k=0, a=2, b=2;
T(n) = O(n02n/2)
= O(2n/2)
More Examples:
- Example-1:
T(n) = 3T(n-1), n>0
= c, n<=0
Sol:a=3, b=1, f(n)=0 so k=0;
Since a>0, T(n) = O(nkan/b)
T(n)= O(n03n/1)
T(n)= 3n
- Example-2:
T(n) = T(n-1) + n(n-1), if n>=2
= 1, if n=1
Sol:a=1, b=1, f(n)=n(n-1) so k=2;
Since a=1, T(n) = O(nk+1)
T(n)= O(n2+1)
T(n)= O(n3)
- Example-3:
T(n) = 2T(n-1) – 1, if n>0
= 1, if n<=0
Sol: This recurrence can’t be solved using above method
since function is not of form T(n) = aT(n-b) + f(n)
Share your thoughts in the comments
Please Login to comment...