Regular Graph in Graph Theory
Last Updated :
04 Sep, 2019
Prerequisite: Graph Theory Basics – Set 1, Set 2
Regular Graph:
A graph is called regular graph if degree of each vertex is equal. A graph is called K regular if degree of each vertex in the graph is K.
Example:
Consider the graph below:

Degree of each vertices of this graph is 2. So, the graph is 2 Regular. Similarly, below graphs are 3 Regular and 4 Regular respectively.
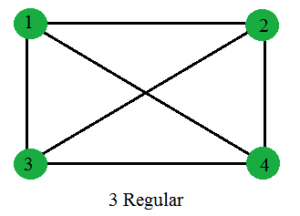
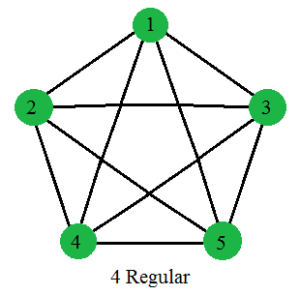
Properties of Regular Graphs:
- A complete graph N vertices is (N-1) regular.
Proof:
In a complete graph of N vertices, each vertex is connected to all (N-1) remaining vertices. So, degree of each vertex is (N-1). So the graph is (N-1) Regular.
- For a K Regular graph, if K is odd, then the number of vertices of the graph must be even.
Proof:
Lets assume, number of vertices, N is odd.
From Handshaking Theorem we know,
Sum of degree of all the vertices = 2 * Number of edges of the graph …….(1)
The R.H.S of the equation (1) is a even number.
For a K regular graph, each vertex is of degree K. Sum of degree of all the vertices = K * N, where K and N both are odd.So their product (sum of degree of all the vertices) must be odd. This makes L.H.S of the equation (1) is a odd number. So L.H.S not equals R.H.S. So our initial assumption that N is odd, was wrong. So, number of vertices(N) must be even.
- Cycle(Cn) is always 2 Regular.
Proof:
In Cycle (Cn) each vertex has two neighbors. So, they are 2 Regular.
- 2 Regular graphs consists of Disjoint union of cycles and Infinite Chains.


- Number of edges of a K Regular graph with N vertices = (N*K)/2.
Proof:
Let, the number of edges of a K Regular graph with N vertices be E.
From Handshaking Theorem we know,
Sum of degree of all the vertices = 2 * E
N * K = 2 * E
or, E = (N*K)/2
- A K-dimensional Hyper cube (Qk) is a K Regular graph.
Below is a 3-dimensional Hyper cube(Q3) which is a 3 Regular graph.

Share your thoughts in the comments
Please Login to comment...