Refractive Index is a property of any material which is used to define the ratio between the speed of light in a medium to the speed in a vacuum. It is denoted by the symbol μ. When travelling in a medium other than the vacuum light particles are absorbed and re-emit by the medium which slows down the speed of light.
Let’s discuss the refractive index and its application and others in detail in this article.
Refraction of Light
It sometimes appears or observed that when the light rays are travelling obliquely from one medium to another medium, the path or direction of the propagation of light in another or second medium somehow changes.
This certain phenomenon is what is known as the refraction of light. It is a very simple word that describes the change in the velocity or speed of light when it goes or travels from one medium to another medium.
The refraction of light depends upon the velocity of the material medium we use and the nature of another medium from which the light comes. There are certain laws for it also which this refraction phenomenon follows. The observable change in the velocity or speed of light rays causes refraction.
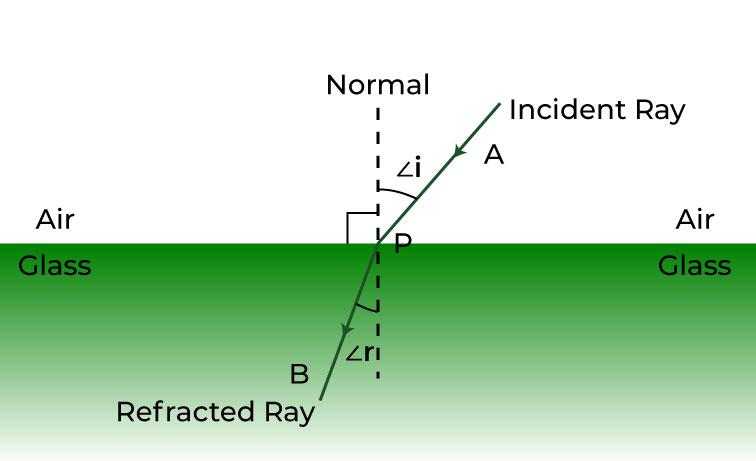
Refraction through two different media or mediums is shown above. The light ray has changed its path on travelling from air to glass, and it will again change when vice versa occurs.
Laws of Refraction
There are given two laws of refraction as stated below which at the sight of refraction the light follows and what we see is the refracted image formed of the object.
- The refracted ray, incident or what we call obliquely falling ray and the normal ray at the point of incidence all will tend to lie together in the same plane.
- Secondly, we have the ratio of the sin of the angle of the incidence and refraction as a constant or has a definite value which is stated or termed as Snell’s law.
sin i / sin r = constant
where
i is the angle of incidence,
r is the angle of refraction,
Constant value depends upon the refractive indexes of the two taken mediums. It is their ratio and is dimensionless.
What is Refractive Index?
Refractive Index first of all is a dimensionless quantity. The index of refraction or in other words refractive index enables us to know how fast light travels through the material medium. The refractive index gives an idea about the speed of light while travelling in a different medium. Whenever the light that tends to travel obliquely from one medium to another changes its direction while travelling from another, the extent of change in the direction of light rays is what we say and calculate as refractive index. The ratio of the velocities or speed of light in different media gives the refractive index.
Refractive index is of two types:
- Absolute Refractive Index
- Relative Refractive Index
The type of refractive index depends upon the two mediums in which the light is travelling. The absolute refractive index has one material medium and one vacuum in which the speed of light is 3 × 108 m/s. The relative refractive index is the relative change in speed or velocity of light upon travelling from one given medium to another.
Upon travelling from a rarer medium to denser the light rays tend to bend towards the normal and if it travels from denser to rarer then it bends away from the normal at the point of incidence.
Absolute Refractive Index
For a considered material medium, the refractive index is observed or considered to be the ratio between the speed or velocity of light in a vacuum (c) to the speed of light in the provided material medium (v) on which it falls. The refractive index or index of refraction for a medium is represented or denoted by small n, and it is given by the following formula:
nv = c / v
where
c is velocity of the light in vacuum
v is velocity of light in the provided medium
The velocity of light in a vacuum is 3 × 108 m/s. Its speed in air is also almost the same as that in a vacuum with a minimal difference. Hence, when travelling from air to the medium the speed is taken to be 3 × 108 m/s only. The absolute refractive index as the name suggests gives us a rough estimate of the optical density of the given material.
The table gives an idea about the absolute refractive indices of different mediums.
|
Material
|
Refractive Index
|
| Air |
1.0003 |
| Water |
1.333 |
| Diamond |
2.417 |
| Ice |
1.31 |
| Ethyl Alcohol |
1.36 |
The one with a higher refractive index is optically denser than a material with a low refractive index which becomes a rarer medium. A material having a higher optical density doesn’t mean it has a high mass by volume density as they are two different quantities.
For instance, kerosene has a lower density than water, but it is optically denser than water as we can see it has a higher value of the refractive index of 1.44 than water 1.33.
Relative Refractive Index
The relative refractive index refers to the refractive index of one material medium with respect to another one. The given velocities of light in different media can give the relative refractive index by the following also where the first medium is not a vacuum:
n21 = v1 / v2
where
n21 is refractive index of the speed of light in material medium 2 with respect to the velocity of light in medium 1
Similarly,
n12 = v2 / v1
where
n12 is refractive index of the speed of light in material medium 1 with respect to the velocity of light in medium 2
On travelling from a rarer to a denser medium, a light ray bends towards normal and vice versa, and on travelling from denser to rarer it bends away from normal. As can be observed and seen that the refractive index of ice is lower than that of kerosene so the light ray after travelling from ice to kerosene has bent towards the normal and so their ratio can give us the relative refractive index.
Check: Refraction Through a Rectangular Glass Slab
Optical Density
A medium, which has a higher refractive index with respect to vacuum is called the optically denser medium. In an optically denser medium, the speed of light is slow in comparison to an optically rarer medium.
Calculation of Refractive Index from the Speed of Light
Refractive Index can easily be calculated when the speed of light is given in two mediums. Let’s take an example, here symbol “n” denotes the refractive index.
Speed of Light (in 1st medium) = v1
Speed of Light (in 2nd medium) = v2
Now, the refractive index (n) of 2nd medium with respect to 1st medium is given by,
n21 = Speed of Light in 1st medium / Speed of light in 2nd medium
n21 = v1/v2
Now, the refractive index (n) of 1st medium with respect to 2nd medium is given by,
n12 = Speed of Light in 2nd medium / Speed of light in 1st medium
n12 = v2 / v1
Why is High Refractive Index Important for Optical Polymers?
High refractive index allows light rays to bend more within the material, which helps to lower the profile of the lens. Thus, by increasing the refractive index, the thickness of the lens decreases which results in lowering the weight of the Optical Polymer.
What is Refractive Index Gradient?
Refractive Index Gradient is the rate of change of the refractive index with respect to the distance travelled in the optical material. The refractive index gradient is expressed as the reciprocal of a unit of distance.
Refractive Index Gradient is the rate of change of refractive index at any point with respect to distance. Refractive Index Gradient is a vector point function.
How Does the Refractive Index Vary with Wavelength?
As we know, the speed of light is the product of frequency and wavelength. The frequency of the light wave is always constant irrespective of the medium it travels, but we know that the velocity of the light changes as it changes the medium, to compensate for the change in velocity wavelength of the light wave changes based on refraction. Hence, we can say that the refractive index of a material varies with the wavelength.
Check: Difference between Wavelength and Frequency
Applications on Refractive Index
Various applications of the Refractive Index are discussed below in the article.
- It is widely used or applied for identifying a particular substance, confirming its purity, or measuring the given concentration.
- Generally, and commonly, it is used for measuring the concentration of the solute in an aqueous solution. For instance, in a solution of sugar, its refractive index of it can be used to determine the sugar content.
- It can also be used also in the determination of the drug concentration in the pharmaceutical or pharmacy industry.
- It is widely used to calculate the focusing power of various lenses, and the dispersive power of prisms.
- It is generally applied for the estimation of the thermophysical properties of many hydrocarbons and petroleum mixtures.
Also, Check
Solved Examples on Refractive Index
Example 1: What is the value of the sin of the angle of incidence if the angle of refraction is given to be 35°? The constant is assumed to be 1.34.
Solution:
As we know,
sin i / sin r = constant
Given constant has value = 1.34 and sin r = sin 35° = 0.57
Putting the respective values of the angles from log table we get
sin i / sin 35° = 1.34
sin i = 1.34 × 0.57
sin i = 0.763
Hence, sin of angle of incidence or sin i = 0.763.
Example 2: What is the constant value if the angle of incidence is 45° and the angle of refraction is given to be 30°?
Solution:
As we know,
sin i / sin r = constant
Given, sin i = sin 45° and sin r = sin 30°
Putting the respective values of the given angles from log table we get
sin 45° / sin 30° = (1/√2) / (1/√3)
= 1.44
Hence, the value of the constant is found to be 1.44.
Example 3: Calculate the speed of light in water and also in ice. The absolute refractive index of ice is 1.31 and water is 1.53. In which medium is the speed highest?
Solution:
As we know,
n = c/v
Refractive index of water n= 1.53, c = 3 × 108 m/s
n = 3 × 108 / vg
vg = 3 × 108 / n
vg = 3 × 108 / 1.53
vg = 1.96 × 108 m/s
Hence, the velocity or speed of light in water is vw = 1.96 × 108 m/s.
Second case,
Refractive index of ice n = 1.31, c = 3 × 108 m/s
n = 3 × 108 / vg
vi = 3 × 108 / n
vi = 3 × 108 / 1.31
vi = 1.96 × 108 m/s
Hence, the velocity or speed of light in ice is vi = 2.29 × 108 m/s.
Therefore, the velocity of light is greater in case of ice than in water.
Example 4: Calculate the speed of light in benzene. The absolute refractive index of benzene is 1.50.
Solution:
As we know we can calculate the refractive index by the following formula,
n = c/v
Refractive index of benzene n= 1.5, c = 3 × 108 m/s
n = 3 × 108 / vb
vb = 3 × 108 / n
vb = 3 × 108 / 1.5
vb = 2 × 108 m/s
Hence, the velocity or speed of light in kerosene is vb = 2 × 108 m/s
Example 5: The velocity of light in kerosene is 2.08 × 108 m/s and in water is 1.96 × 108 m/s. By referring to the given values calculate or find the refractive index of the kerosene with respect to the water medium.
Solution:
As we know,
n21 = v1 / v2
nkw = vw / vk
vk = 2.08 × 108 m/s
vw = 1.96 × 108 m/s
nkw = 2.08 × 108 m/s / 1.96 × 108 m/s
nkw = 0.94
Hence, the refractive index ratio of kerosene in respect to second medium water is 0.94.
Related Article:
Conclusion of Refractive Index
The refractive index defines how light bends or changes direction as it travels through various materials. It is essential for many applications, such as the study of optical phenomena including dispersion and total internal reflection, as well as lenses, prisms, and fiber optics.
Refractive Index- FAQs
What is a Refractive Index?
Light travelling from one medium to another medium bends accordingly. The bending of a light ray is measured by the relative refractive index of the medium. It is also defined as the ratio of the velocity of a light ray in a vacuum to the velocity of light in the medium, It is denoted by n, n = c/v.
What is the Unit of Refractive Index?
The refractive index is defined as the ratio of two velocities. Thus, we can say that the refractive index is a dimensionless or unitless quantity.
What is the refractive index of water?
The refractive index of water with respect to vacuum is 1.333.
What is the formula to calculate the refractive index of a medium?
The formula to calculate the refractive index of a medium is given below,
n = c / v
where
n is the refractive index of the medium
c is the velocity of light in vacuum
v is the velocity of light in the medium
Is the speed of light faster in glass or water?
The refractive index of water is 1.3 and the refractive index of glass is 1.5. we know that a higher refractive index lowers the speed of light. Thus, it is evident that the speed of light is faster in water than in glass.
Share your thoughts in the comments
Please Login to comment...