The light gets reflected or refracted from the surfaces or medium. Any surface which is polished or in other words shiny always acts like a mirror be it of any kind. The observation of light bouncing off or getting back from the surfaces is termed as reflection. The light after the case of reflection travels or follows in the same medium from where the ray was incident on the surface. This phenomenon of reflection does not intend to change the velocity of light it only reverses the direction of light incident on it. This can be observed on any surface which is rough or smooth. The path of the reflected ray will depend upon the extent of smoothness of the surface, in the case of a smooth surface the reflected ray emerges with the same angle as of incidence and in the latter case suffers irregular reflection and so the reflected ray doesn’t emerge same as that of incidence angle. On the other view, light can also change its speed when traveling from one medium to another which is known as refraction of light.
Spherical Mirrors
The curved surface we see of a shining spoon can be considered a curved mirror. The most widely used type of curved mirror is the spherical mirror. The reflecting surface of such mirrors is considered to form a part of the surface of any sphere. Those mirrors which possess a reflecting surfaces which are spherical, are called spherical mirrors.
There are two types of spherical mirrors for which the mirror formula is used.
Concave mirror or also called the converging mirror which have an inward bent surface. They have a negative value of focal length in sign convention and can form both virtual and real images based on the position of the object.
|
| Within focus ( Between pole P and focus F) | Behind the mirror | Enlarged | Virtual and erect |
| At focus | At infinity | Highly Enlarge | Real and Inverted |
| Between F and C | Beyond C | Enlarged | Real and Inverted |
| At C | At C | Equal to object | Real and Inverted |
| Beyond C | Between F and C | Diminished | Real and Inverted |
| At Infinity | At focus | Highly diminished (Pointed Size) | Real and Inverted |
Convex mirror or also called the diverging mirror has a bulged outward surface. They have a positive value of focal length from sign convention. They can only form virtual and erect images which can be enlarged or diminished depending on the position of the object placed.
|
| Anywhere between pole P and Infinity | Behind the mirror between P and F | Diminished | Virtual and erect |
| At infinity | Behind the mirror at Focus | Highly diminished | Virtual and erect |
Sign Convention Chart for Reference
These are to be noted very specifically while doing sums on mirror formula as well as on magnification. Remember to put the values using the sign conventions otherwise, there will be high chances of any error while solving questions related to the spherical mirrors concave or convex.

Mirror Formula
To do the sums related to the spherical mirrors, the formula used is known as mirror formula. It is used to calculate the focal length, image distance, object distance and also the magnification or any other thing required. We usually put the formula first and then put the signs so as to do the sums to minimize any error which can be generated. The sign conventions which are to be followed while using mirror formula are fixed so from the above given diagram we can easily put the signs according to the requirement to get the required result.
Usually if the object is located on the left side of principal axis from the mirror then the object distance is taken negative. While if it is located on the right side it is taken to be positive. The sign of focal length depends on the type of the mirror we are using, as for the concave mirror it is negative and for the convex mirror on the other hand is positive always. It is to be mentioned again that we have to follow the sign conventions strictly to get the correct answer.
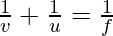
Where u = object distance, v = image distance, f = focal length of mirror
What is Magnification?
Magnification is termed as the increase in the image size produced by spherical mirrors concave or convex with respect to the object size. It is considered to be the ratio of the height of the image to the height of the object and is denoted as m.
Magnification Formula
The magnification which is represented by the letter small m produced by a spherical mirror can be expressed or represented as:
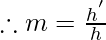
Where the letter h is the height of the image and h’ is the height of the object.
Magnification is also equal to the ratio of the image distance from the pole of the mirror to the object distance taken from the pole of the mirror.
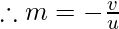
As the object lies always above the main principal axis, the height of the object is taken always as positive. But the sign for the image height may change according to the type of image formed in case of any type of mirror chosen. The height of the virtual images formed should be taken as positive while the height of the real images formed should be taken as negative.
Uses of Magnification
- A precision magnifier performs the role of a very simple magnifier, but it holds multiple elements to erase the aberrations and yield a sharper image for us.
- A tiny water droplet acts as a very simple magnifier that magnifies the object present behind it. The water forms small spherical droplets due to the influence of the surface tension. When the water droplet is in contact with any object, a spherical shape is distorted but capable of forming a good image of the object.
Points to Remember
- The positive magnitude or value of the magnification indicates or tells that a virtual and erect image is formed.
- The negative magnitude or value of the magnification indicates or tells that a real and inverted image is formed.
Examples on Magnification Formula
Example 1: What is the magnification produced if the image distance is 6 cm and the object is located at 12 cm in case of concave mirror?
Solution:
As we know the magnification can be calculated using the following formula;
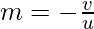
Given, v= -6cm and u= -12cm the signs are given using sign convention.
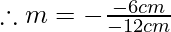
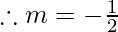
m = -0.5
Hence, there is a decrease by a factor of 0.5.
Example 2: What is the image distance in case of convex mirror if the object is placed at 12cm? Determine it if the height of the image if 4 cm and height of the object is 2 cm.
Solution:
As we know the magnification can be calculated using the following formulas;
m 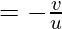 and also m
and also m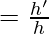
Given, height of image h’ = 4cm, height of object{h}= 2cm and u= -12cm the signs are given using sign convention.
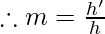
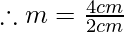
m = +2
Hence, there is an increase by a factor of 2.
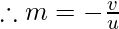
Putting m= 2 and u=-12cm we get
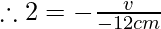
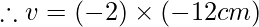
v= 24cm
Hence, the image distance is 24cm.
Example 3: What is the magnification produced if the image distance is 12 cm and the object is located at 6 cm in case of convex mirror?
Solution:
As we know the magnification can be calculated using the following formula;
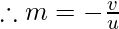
Given, v= 12cm and u= -6cm the signs are given using sign convention.
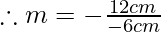
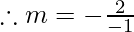
m = 2
Hence, the magnification is 2.
Example 4: What is the increase or decrease in the magnification if the object is located at 7 cm in front of a concave mirror and the image is formed at 14 cm?
Solution:
As we know the magnification can be calculated using the following formula;
m=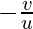
Given, v= -14 cm and u= -7 cm the signs are given using sign convention.
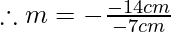
m=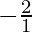
m=-2
Hence, there is an increase by a factor of 0.5.
Example 5: What is the magnification if the object height is 6 cm and the image height is 24 cm below the principal axis?
Solution:
As we know the magnification can be calculated using the following formula;
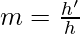
Given, height of image h’ = -24 cm, height of object{h}= 6cm the signs are given using sign convention.
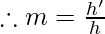
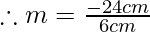
m=-4
Hence, the magnification is (-4).
Example 6: What is the magnification if the object height is 6 cm and the image height is 18 cm above the principal axis?
Solution:
As we know the magnification can be calculated using the following formula;
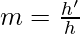
Given, height of image h’ = 18cm, height of object{h}= 6cm the signs are given using sign convention.
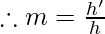
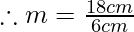
m=+3
Hence, the magnification is 3.
Example 7: What is the image distance in case of concave mirror if the object distance is 8 cm? It is given that the focal length of the mirror is 4 cm.
Solution:
As we know from mirror formula,
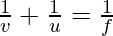
Where u= object distance= -8cm
v= image distance=?
f= focal length of mirror= -4cm
Putting values we get
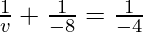
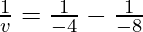
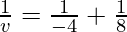
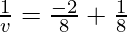
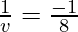
v= -8 cm
Hence, the object is located 8 cm in front of the mirror.
Example 8: What is the image distance in case of convex mirror if the object distance is 10 cm? It is given that the focal length of the mirror is 10 cm.
Solution:
As we know from mirror formula,
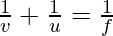
Where u= object distance= -10cm
v= image distance=?
f= focal length of mirror= +10cm
Putting values we get
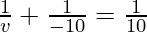
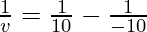
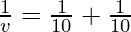
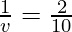
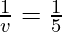
v= 5 cm
Hence, the image is located 5 cm behind the mirror.
Example 9: What is the image distance in case of concave mirror if the object distance is 11 cm? It is given that the focal length of the mirror is 11 cm.
Solution:
As we know from mirror formula,
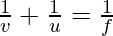
Where u = object distance= -11cm
v= image distance=?
f= focal length of mirror= -11cm
Putting values we get
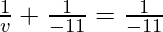
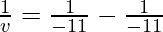
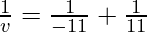
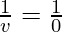
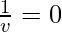
v= infinity
Hence, the image will be formed at infinity.
Share your thoughts in the comments
Please Login to comment...