Quotient and remainder dividing by 2^k (a power of 2)
Last Updated :
23 Sep, 2022
Given a positive integer n as a dividend and another number m (a form of 2^k), find the quotient and remainder without performing actual division
Examples:
Input : n = 43, m = 8
Output : Quotient = 5, Remainder = 3
Input : n = 58, m = 16
Output : Quotient = 3, Remainder = 10
An approach using bitwise operation
In this, we are using a bitwise representation of a number for understanding the role of division of any number by divisor of form 2^k. All numbers which are power of two include only 1 set bits in their representation and we will use this property.
For finding the remainder we will take logical AND of the dividend (n) and divisor minus 1 (m-1), this will give only the set bits of dividend right to the set bit of divisor which is our actual remainder in that case.
Further, the left part of the dividend (from the position of set bit in divisor) would be considered for quotient. So, from dividend (n) removing all bits right from the position of set bit of divisor will result in the quotient, and right shifting the dividend log2(m) times will do this job for finding the quotient.
- Remainder = n & (m-1)
- Quotient = (n >> log2(m) )
Note: Log2(m) will give the number of bits present in the binary representation of m.
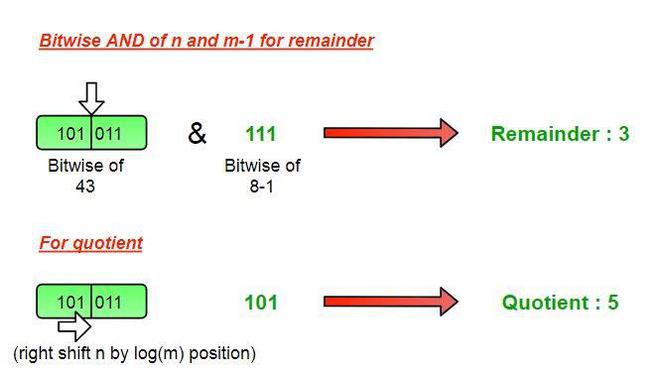
Finding Quotient and Remainder
Below is the implementation:
C++
#include<bits/stdc++.h>
using namespace std;
void divide(int n,int m)
{
cout <<"Remainder = " << ((n) &(m-1));
cout <<"\nQuotient = " <<(n >> (int)(log2(m)));
}
int main()
{
int n = 43, m = 8;
divide(n, m);
return 0;
}
|
Java
import java.io.*;
public class GFG {
static void divide(int n, int m)
{
System.out.println("Remainder = "
+ ((n) &(m-1)));
System.out.println("Quotient = "
+ (n >> (int)(Math.log(m) / Math.log(2))));
}
static public void main (String[] args)
{
int n = 43, m = 8;
divide(n, m);
}
}
|
Python 3
import math
def divide(n, m):
print("Remainder = ",
((n) &(m-1)))
print("Quotient = " ,(n >>
(int)(math.log2(m))))
n = 43
m = 8
divide(n, m)
|
C#
using System;
public class GFG
{
static void divide(int n,int m)
{
Console.WriteLine("Remainder = " +((n) & (m - 1)));
Console.WriteLine("Quotient = "
+ (n >> (int)(Math.Log(m))));
}
static public void Main ()
{
int n = 43, m = 8;
divide(n, m);
}
}
|
PHP
<?php
function divide($n,$m)
{
echo "Remainder = ". (($n) &($m - 1));
echo "\nQuotient = ".($n >> (int)(log($m, 2)));
}
$n = 43;
$m = 8;
divide($n, $m);
?>
|
Javascript
<script>
function divide(n, m)
{
document.write("Remainder = "
+ ((n) &(m-1)) + "<br/>");
document.write("Quotient = "
+ (n >> (Math.log(m) / Math.log(2))));
}
let n = 43, m = 8;
divide(n, m);
</script>
|
Output
Remainder = 3
Quotient = 5
Time Complexity: O(1)
Auxiliary Space: O(1)
Share your thoughts in the comments
Please Login to comment...