Queries to count points lying on or inside an isosceles Triangle with given length of equal sides

Given an array arr[][] of dimension N * 2 representing the co-ordinates of N points and an array Q[] consisting of M integers, the task for every element in the Q[i] is to find the number of points lying inside or on the right-angled isosceles triangle formed on the positive co-ordinate axis with two equal sides of length Q[i]in each query.

Examples:

Input: N = 4, arr[][] = { {2.1, 3.0}, {3.7, 1.2}, {1.5, 6.5}, {1.2, 0.0} }, Q[] = { 2, 8, 5}, M = 3
Output: 1 4 2
Explanation:

• First query: The point (1.2, 0.0) lies inside the triangle.
• Second query: The points { (2.1, 3.0), (3.7, 1.2), (1.2, 0.0) } lies inside the triangle and point (1.5, 6.5) lies on the triangle.
• Third query: The points {(3.7, 1.2), (1.2, 0.0)} lies inside the triangle.

Input: N = 3, arr[][] = { {0, 0}, {1, 1}, {2, 1} }, Q[] = {1, 2, 3}, M = 3
Output: 1 2 3
Explanation:

• First query: The point (0, 0) lies inside the triangle.
• Second query: The points { (0, 0), (1, 1) } lies inside the triangle.
• Third query: All the points lies inside the triangle.

Naive Approach: The simplest approach is to in each query traverse the array of points and checks if it lies inside the right-angled triangle formed. After completing the above steps, print the count. 
Time Complexity: O(N * M)
Auxiliary Space: O(1)

Efficient Approach: The above approach can be optimized based on the following observations:

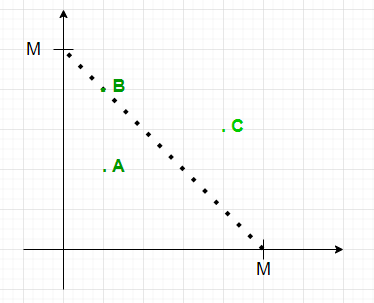
• A point (x, y) lies inside the isosceles right angle triangle formed on co-ordinate axis whose two equal sides are X if :
  • x ≥ 0 && y ≥ 0 && x + y ≤ X
• By pre-storing the count of points with coordinates sum ≤ X, the query can be answered in constant time.

Follow the steps below to solve the problem:

• Initialize an array, say pre[] of max size, to store the count of points whose sum of coordinates is less than or equal to the index of the array.
• Traverse the array arr[][] and increment the count of ceil(arr[i][0] + arr[i][1]) by 1.
• Calculate the prefix sum array of array pre[].
• Traverse the array Q[] and print the pre[Q[i]].

Below is the implementation of the above approach:

C++

// C++ implementation of above approach

#include <bits/stdc++.h>
using namespace std;

int const MAX = 1e6 + 5;

// Function to find answer of each query
int query(vector<vector<float> > arr,
          vector<int> Q)
{
    // Stores the count of points with sum
    // less than or equal to their indices
    int pre[MAX] = { 0 };

    // Traverse the array
    for (int i = 0; i < arr.size(); i++) {

        // If both x and y-coordinate < 0
        if (arr[i][0] < 0 || arr[i][1] < 0)
            continue;

        // Stores the sum of co-ordinates
        int sum = ceil((arr[i][0] + arr[i][1]));

        // Increment count of sum by 1
        pre[sum]++;
    }

    // Prefix array
    for (int i = 1; i < MAX; i++)
        pre[i] += pre[i - 1];

    // Perform queries
    for (int i = 0; i < Q.size(); i++) {
        cout << pre[Q[i]] << " ";
    }
    cout << endl;
}
// Drivers Code
int main()
{
    vector<vector<float> > arr = { { 2.1, 3.0 },
                                   { 3.7, 1.2 },
                                   { 1.5, 6.5 },
                                   { 1.2, 0.0 } };
    vector<int> Q = { 2, 8, 5 };
    int N = arr.size();
    int M = Q.size();

    query(arr, Q);
}

Java

// Java implementation of above approach
import java.util.*;
class GFG
{

static int MAX = (int) (1e6 + 5);

// Function to find answer of each query
static void query(double [][]arr,
          int []Q)
{

    // Stores the count of points with sum
    // less than or equal to their indices
    int pre[] = new int[MAX];

    // Traverse the array
    for (int i = 0; i < arr.length; i++)
    {

        // If both x and y-coordinate < 0
        if (arr[i][0] < 0 || arr[i][1] < 0)
            continue;

        // Stores the sum of co-ordinates
        int sum = (int) Math.ceil((arr[i][0] + arr[i][1]));

        // Increment count of sum by 1
        pre[sum]++;
    }

    // Prefix array
    for (int i = 1; i < MAX; i++)
        pre[i] += pre[i - 1];

    // Perform queries
    for (int i = 0; i < Q.length; i++)
    {
        System.out.print(pre[Q[i]]+ " ");
    }
    System.out.println();
}

// Drivers Code
public static void main(String[] args)
{
    double[][] arr = { { 2.1, 3.0 },
                                   { 3.7, 1.2 },
                                   { 1.5, 6.5 },
                                   { 1.2, 0.0 } };
    int []Q = { 2, 8, 5 };
    int N = arr.length;
    int M = Q.length;

    query(arr, Q);
}
}

// This code is contributed by 29AjayKumar

Python3

# Python3 implementation of above approach
MAX = 10**6 + 5
from math import ceil

# Function to find answer of each query
def query(arr, Q):

    # Stores the count of points with sum
    # less than or equal to their indices
    pre = [0]*(MAX)

    # Traverse the array
    for i in range(len(arr)):

        #` If both x and y-coordinate < 0
        if (arr[i][0] < 0 or arr[i][1] < 0):
            continue

        # Stores the sum of co-ordinates
        sum = ceil((arr[i][0] + arr[i][1]));

        # Increment count of sum by 1
        pre[sum] += 1

    # Prefix array
    for i in range(1, MAX):
        pre[i] += pre[i - 1]

    # Perform queries
    for i in range(len(Q)):
        print(pre[Q[i]], end = " ")

# Drivers Code
if __name__ == '__main__':
    arr = [[ 2.1, 3.0],
          [ 3.7, 1.2],
          [ 1.5, 6.5],
          [ 1.2, 0.0]]
    Q = [2, 8, 5]
    N = len(arr)
    M = len(Q)

    query(arr, Q)

    # This code is contributed by mohit kumar 29.

C#

// C# implementation of above approach
using System;
public class GFG
{

  static int MAX = (int) (1e6 + 5);

  // Function to find answer of each query
  static void query(double [,]arr,
                    int []Q)
  {

    // Stores the count of points with sum
    // less than or equal to their indices
    int []pre = new int[MAX];

    // Traverse the array
    for (int i = 0; i < arr.GetLength(0); i++)
    {

      // If both x and y-coordinate < 0
      if (arr[i,0] < 0 || arr[i,1] < 0)
        continue;

      // Stores the sum of co-ordinates
      int sum = (int) Math.Ceiling((arr[i,0] + arr[i,1]));

      // Increment count of sum by 1
      pre[sum]++;
    }

    // Prefix array
    for (int i = 1; i < MAX; i++)
      pre[i] += pre[i - 1];

    // Perform queries
    for (int i = 0; i < Q.Length; i++)
    {
      Console.Write(pre[Q[i]]+ " ");
    }
    Console.WriteLine();
  }

  // Drivers Code
  public static void Main(String[] args)
  {
    double[,] arr = { { 2.1, 3.0 },
                     { 3.7, 1.2 },
                     { 1.5, 6.5 },
                     { 1.2, 0.0 } };
    int []Q = { 2, 8, 5 };
    int N = arr.GetLength(0);
    int M = Q.Length;
    query(arr, Q);
  }
}

// This code is contributed by 29AjayKumar

Javascript

<script>
// Javascript implementation of above approach

let MAX =  (1e6 + 5)

// Function to find answer of each query
function query(arr,Q)
{
    // Stores the count of points with sum
    // less than or equal to their indices
    let pre = new Array(MAX);
     for(let i=0;i<MAX;i++)
        pre[i]=0;
    // Traverse the array
    for (let i = 0; i < arr.length; i++)
    {

        // If both x and y-coordinate < 0
        if (arr[i][0] < 0 || arr[i][1] < 0)
            continue;

        // Stores the sum of co-ordinates
        let sum = Math.ceil((arr[i][0] + arr[i][1]));

        // Increment count of sum by 1
        pre[sum]++;
    }

    // Prefix array
    for (let i = 1; i < MAX; i++)
        pre[i] += pre[i - 1];

    // Perform queries
    for (let i = 0; i < Q.length; i++)
    {
        document.write(pre[Q[i]]+ " ");
    }
    document.write("<br>");
}
// Drivers Code
let arr=[[ 2.1, 3.0 ],
                                   [ 3.7, 1.2 ],
                                   [ 1.5, 6.5 ],
                                   [ 1.2, 0.0 ] ];

let Q=[2, 8, 5];
let N = arr.length;
let M = Q.length;
query(arr, Q);

// This code is contributed by unknown2108
</script>

Output:

1 4 2

Time Complexity: O(N)
Auxiliary Space: O(N)