Python Program to check Involutory Matrix
Last Updated :
30 Dec, 2022
Given a matrix and the task is to check matrix is an involutory matrix or not.
Involutory Matrix: A matrix is said to be an involutory matrix if the matrix multiplies by itself and returns the identity matrix. The involutory matrix is the matrix that is its own inverse. The matrix A is said to be an involutory matrix if A * A = I. Where I is the identity matrix.
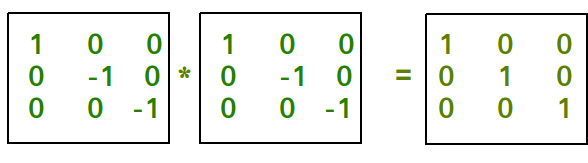
Examples:
Input : mat[N][N] = {{1, 0, 0},
{0, -1, 0},
{0, 0, -1}}
Output : Involutory Matrix
Input : mat[N][N] = {{1, 0, 0},
{0, 1, 0},
{0, 0, 1}}
Output : Involutory Matrix
Python3
N = 3;
def multiply(mat, res):
for i in range(N):
for j in range(N):
res[i][j] = 0;
for k in range(N):
res[i][j] += mat[i][k] * mat[k][j];
return res;
def InvolutoryMatrix(mat):
res=[[0 for i in range(N)]
for j in range(N)];
res = multiply(mat, res);
for i in range(N):
for j in range(N):
if (i == j and res[i][j] != 1):
return False;
if (i != j and res[i][j] != 0):
return False;
return True;
mat = [[1, 0, 0], [0, -1, 0], [0, 0, -1]];
if (InvolutoryMatrix(mat)):
print("Involutory Matrix");
else:
print("Not Involutory Matrix");
|
Time Complexity: O(N3)
Auxiliary Space: O(N2)
Please refer complete article on Program to check Involutory Matrix for more details!
Using Numpy:
Note: Before running the code please install the Numpy library using the command below
pip install numpy
Another approach is to use the numpy library to check if the matrix is involutory. This can be done by using the numpy.allclose function to compare the matrix with its inverse.
For example, the following code snippet checks if a matrix is involutory:
Python3
import numpy as np
def is_involutory(matrix):
inverse = np.linalg.inv(matrix)
return np.allclose(matrix, inverse)
matrix = np.array([[1, 0, 0], [0, -1, 0], [0, 0, -1]])
print(is_involutory(matrix))
|
Output: True
This approach has the advantage of being more concise and easier to read, and it also takes advantage of the optimized linear algebra routines provided by numpy. Space complexity is O(N^2) and the time complexity of this approach will depend on the complexity of the matrix inverse calculation, which is generally O(N^3) for dense matrices.
Share your thoughts in the comments
Please Login to comment...