Python | Implementing 3D Vectors using dunder methods

Last Updated : 31 May, 2021

Dunder methods (double underscore) in Python are methods which are commonly used for operator overloading. Some examples of dunder methods are __init__ , __repr__ , __add__ , __str__ etc. These methods are useful to modify the behavior of an object.
For example, when ‘+’ operator is used between two numbers, the result obtained is simply the addition of the two numbers whereas when ‘+’ is used between two strings, the result obtained is the concatenation of the two strings.
Commonly used Vector operations:
Consider two vectors vec1 and vec2 with co-ordinates: vec1 = (x1, y1, z1) and vec2 = (x2, y2, z2).

Magnitude: Magnitude of vec1 = $\sqrt{(x1)^2 + (y1)^2 + (z1)^2}$ .
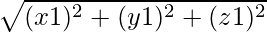Addition: For this operation, we need __add__ method to add two Vector objects.
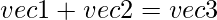$vec1 + vec2 = vec3$ where co-ordinates of vec3 are $(x1+x2, y1+y2, z1+z2)$ .
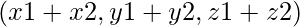Subtraction: For this operation, we need __sub__ method to subtract two Vector objects.
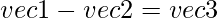$vec1 - vec2 = vec3$ where co-ordinates of vec3 are $(x1-x2, y1-y2, z1-z2)$ .
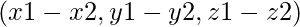Dot Product: For this operation, we need the __xor__ method as we are using ‘^’ symbol to denote the dot product. 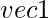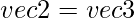$vec1$ ^ $vec2 = vec3$ where co-ordinates of vec3 are $(x1*x2, y1*y2, z1*z2)$ .
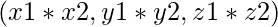Cross Product: For this operation, we need the __mul__ method as we are using ‘*’ symbol to denote the cross product. 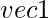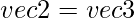$vec1$ * $vec2 = vec3$ where co-ordinates of vec3 are $(y1*z2 - y2*z1, x1*z2 - x2*z1, x1*y2 - x2*y1)$ .

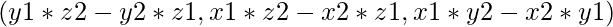Finally, we also need a __init__ method to initialize the Vector co-ordinates and the __repr__ method to define the representation of the Vector object. So when we print our Vector object, the output should be something like this. print(Vector(1, -2, 3)) ==> Output: 1i -2j + 3k
Below is the implementation :

Python3

# Python3 program to implement 3-D Vectors.
from math import sqrt
 
# Definition of Vector class
class Vector:
 
    # Initialize 3D Coordinates of the Vector
    def __init__(self, x, y, z):
        self.x = x
        self.y = y
        self.z = z
 
    # Method to calculate magnitude of a Vector
    def magnitude(self):
 
        return sqrt(self.x ** 2 + self.y ** 2 + self.z ** 2)
 
    # Method to add to Vector
    def __add__(self, V):
 
        return Vector(self.x + V.x, self.y + V.y, self.z + V.z)
 
    # Method to subtract 2 Vectors
    def __sub__(self, V):
 
        return Vector(self.x - V.x, self.y - V.y, self.z - V.z)
 
    # Method to calculate the dot product of two Vectors
    def __xor__(self, V):
 
        return self.x * V.x + self.y * V.y + self.z * V.z
 
    # Method to calculate the cross product of 2 Vectors
    def __mul__(self, V):
 
        return Vector(self.y * V.z - self.z * V.y,
                      self.z * V.x - self.x * V.z,
                      self.x * V.y - self.y * V.x)
 
    # Method to define the representation of the Vector
    def __repr__(self):
 
        out = str(self.x) + "i "
 
        if self.y >= 0:
            out += "+ "
        out += str(self.y) + "j "
        if self.z >= 0:
            out += "+ "
        out += str(self.z) + "k"
 
        return out
 
 
if __name__ == "__main__":
 
    vec1 = Vector(1, 2, 2)
    vec2 = Vector(3, 1, 2)
 
    # Magnitude of vector1
    print("Magnitude of vector1:", vec1.magnitude())
 
    # String representation of vector
    print("String representation of vector1: " + str(vec1))
 
    # Addition of two vectors
    print("Addition of vector1 and vector2: " + str(vec1 + vec2))
 
    # Subtraction of two vectors
    print("Subtraction of vector1 and vector2: " + str(vec1 - vec2))
 
    # Dot product of two vectors
    print("Dot Product of vector1 and vector2: " + str(vec1 ^ vec2))
 
    # Cross product of two vectors
    print("Cross Product of vector1 and vector2: " + str(vec1 * vec2))

Output

Magnitude of vector1: 3.0
String representation of vector1: 1i + 2j + 2k
Addition of vector1 and vector2: 4i + 3j + 4k
Subtraction of vector1 and vector2: -2i + 1j + 0k
Dot Product of vector1 and vector2: 9
Cross Product of vector1 and vector2: 2i + 4j -5k

Attention geek! Strengthen your foundations with the Python Programming Foundation Course and learn the basics.

To begin with, your interview preparations Enhance your Data Structures concepts with the Python DS Course. And to begin with your Machine Learning Journey, join the Machine Learning – Basic Level Course

My Personal Notes

Related Articles

Python | Implementing 3D Vectors using dunder methods

Python3