Puzzle | 1000 light bulbs switched on/off by 1000 people passing by
Last Updated :
05 Jul, 2021
There are 1000 light bulbs and 1000 people. All light bulbs are initially off. Person 1 goes flipping light bulb 1, 2, 3, 4, … person 2 then flips 2, 4, 6, 8, … person 3 then 3, 6, 9, … etc until all 1000 persons have done this. What is the status of light bulbs 25, 93, 576, 132, 605, 26, 45, 37, 36 after all people have flipped their respective light bulbs? Is there a general solution to predict the status of a light bulb? How many light bulbs are on after all 1000 people have gone by?
Explanation: The key observations are:
- Person 1 flips the light bulb 1, 2, 3, … which are multiples of 1.
- Person 2 flips the light bulb 2, 4, 6, … which are multiples of 2.
- Person 3 flips the light bulb 3, 6, 9, … which are multiples of 3.
- Similarly, Person 1000 flips the light bulb 1000, which is a multiple of 1000.
- From the above observations, we can say that person i will flip light bulbs which are multiples of i,
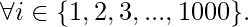
- Thus, a light bulb j will be flipped by all persons for whom j is a multiple of their person number. In other words, light bulb j will be flipped by all people whose for person number i is a factor of j,

- Examples:
- (i) Light Bulb 10 will be flipped by persons 1, 2, 5, 10 whose person numbers are factors of 10.
- (ii) Light Bulb 12 will be flipped by persons 1, 2, 3, 4, 6, 12 whose person numbers are factors of 12.
- Thus, light bulb 25 will be flipped by persons 1, 5, 25, so it will be flipped 3 times, which is odd and since initially, all bulbs were “off”, now light bulb 25 will be “on”.
- The light bulb 93 will be flipped by persons 1, 3, 31, 93, so it will be flipped 4 times, which is even and since initially, all bulbs were “off”, now light bulb 93 will be “off”.
- The light bulb 576 will be flipped by persons 1, 2, 3, 4, 6, 8, 9, 12, 16, 18, 24, 32, 36, 48, 64, 72, 96, 144, 192, 288, 576, so it will be flipped 21 times, which is odd and since initially, all bulbs were “off”, now light bulb 576 will be “on”.
- The light bulb 132 will be flipped by persons 1, 2, 3, 4, 6, 11, 12, 22, 33, 44, 66, 132, so it will be flipped 12 times, which is even and since initially, all bulbs were “off”, now light bulb 132 will be “off”.
- The light bulb 605 will be flipped by persons 1, 5, 11, 55, 121, 605, so it will be flipped 6 times, which is even and since initially, all bulbs were “off”, now light bulb 605 will be “off”.
- The light bulb 26 will be flipped by persons 1, 2, 13, 26, so it will be flipped 4 times, which is even and since initially, all bulbs were “off”, now light bulb 26 will be “off”.
- The light bulb 45 will be flipped by persons 1, 3, 5, 9, 15, 45, so it will be flipped 6 times, which is even and since initially, all bulbs were “off”, now light bulb 45 will be “off”.
- The light bulb 37, being the prime numbered bulb, will be flipped by persons 1, 37, so it will be flipped 2 times, which is even and since initially, all bulbs were “off”, now light bulb 37 will be “off”.
- The light bulb 36 will be flipped by persons 1, 2, 3, 4, 6, 9, 12, 18, 36, so it will be flipped 9 times, which is odd and, since initially, all bulbs were “off”, now light bulb 36 will be “on”.
To find out the status of a given light bulb:
We count the number of factors of the light bulb number, and as per the above observations, if the number of factors is odd, then the light bulb will be “on”, and if it’s even, then it will be “off” in the end.
Algorithm to find how many light bulbs will be “on” in the end:
We count the factors of each number from 1 to 1000. If the number of factors for any number is odd, the corresponding light bulb is “on” so we update the result, and finally, print it.
Below is the code implementing the above algorithm.
C++
#include <iostream>
using namespace std;
int findOnBulbs(int numberOfBulbs)
{
int onBulbs = 0;
int bulb = 1;
int person = 1;
for (bulb = 1; bulb <= numberOfBulbs; bulb++) {
int factors = 0;
for (person = 1; person * person <= numberOfBulbs; person++) {
if (bulb % person == 0)
{
factors++;
if (bulb / person != person)
{
factors++;
}
}
}
if (factors % 2 == 1)
{
cout << "Light bulb "
<< bulb
<< " will be on"
<< "\n";
onBulbs++;
}
}
return onBulbs;
}
int main()
{
int numberOfBulbs = 1000;
int onBulbs = findOnBulbs(numberOfBulbs);
cout << "Total "
<< onBulbs
<< " light bulbs will be on in the end out of "
<< numberOfBulbs
<< " light bulbs"
<< "\n";
return 0;
}
|
Java
public class GFG
{
static int findOnBulbs(int numberOfBulbs)
{
int onBulbs = 0;
int bulb = 1;
int person = 1;
for (bulb = 1; bulb <= numberOfBulbs; bulb++) {
int factors = 0;
for (person = 1; person * person <= numberOfBulbs; person++) {
if (bulb % person == 0)
{
factors++;
if (bulb / person != person)
{
factors++;
}
}
}
if (factors % 2 == 1)
{
System.out.println("Light bulb " + bulb + " will be on");
onBulbs++;
}
}
return onBulbs;
}
public static void main(String [] args)
{
int numberOfBulbs = 1000;
int onBulbs = findOnBulbs(numberOfBulbs);
System.out.println("Total " + onBulbs
+ " light bulbs will be on in the end out of "
+ numberOfBulbs + " light bulbs");
}
}
|
Python3
def findOnBulbs(numberOfBulbs):
onBulbs = 0
bulb = 1
person = 1
for bulb in range(1, numberOfBulbs + 1):
factors = 0
for person in range(1, int(numberOfBulbs**(0.5)) + 1):
if bulb % person == 0:
factors += 1
if bulb // person != person:
factors += 1
if factors % 2 == 1:
print("Light bulb", bulb, "will be on")
onBulbs += 1
return onBulbs
if __name__ == "__main__":
numberOfBulbs = 1000
onBulbs = findOnBulbs(numberOfBulbs)
print("Total", onBulbs, "light bulbs will",
"be on in the end out of",
numberOfBulbs, "light bulbs")
|
C#
using System;
class GFG
{
static int findOnBulbs(int numberOfBulbs)
{
int onBulbs = 0;
int bulb = 1;
int person = 1;
for (bulb = 1; bulb <= numberOfBulbs; bulb++) {
int factors = 0;
for (person = 1; person * person <= numberOfBulbs; person++) {
if (bulb % person == 0)
{
factors++;
if (bulb / person != person)
{
factors++;
}
}
}
if (factors % 2 == 1)
{
Console.WriteLine("Light bulb " + bulb + " will be on");
onBulbs++;
}
}
return onBulbs;
}
public static void Main()
{
int numberOfBulbs = 1000;
int onBulbs = findOnBulbs(numberOfBulbs);
Console.WriteLine("Total " + onBulbs
+ " light bulbs will be on in the end out of "
+ numberOfBulbs + " light bulbs");
}
}
|
PHP
<?php
function findOnBulbs($numberOfBulbs)
{
$onBulbs = 0;
$bulb = 1;
$person = 1;
for ($bulb = 1;
$bulb <= $numberOfBulbs; $bulb++)
{
$factors = 0;
for ($person = 1;
$person * $person <= $numberOfBulbs; $person++)
{
if ($bulb % $person == 0)
{
$factors++;
if ($bulb / $person != $person)
{
$factors++;
}
}
}
if ($factors % 2 == 1)
{
echo "Light bulb " . $bulb .
" will be on" ."\n";
$onBulbs++;
}
}
return $onBulbs;
}
$numberOfBulbs = 1000;
$onBulbs = findOnBulbs($numberOfBulbs);
echo "Total " . $onBulbs . " light bulbs will " .
"be on in the end out of " . $numberOfBulbs .
" light bulbs" ."\n";
?>
|
Javascript
<script>
function findOnBulbs(numberOfBulbs)
{
let onBulbs = 0;
let bulb = 1;
let person = 1;
for (bulb = 1; bulb <= numberOfBulbs; bulb++) {
let factors = 0;
for (person = 1; person * person <= numberOfBulbs; person++) {
if (bulb % person == 0)
{
factors++;
if (bulb / person != person)
{
factors++;
}
}
}
if (factors % 2 == 1)
{
document.write("Light bulb " + bulb + " will be on<br>");
onBulbs++;
}
}
return onBulbs;
}
let numberOfBulbs = 1000;
let onBulbs = findOnBulbs(numberOfBulbs);
document.write("Total " + onBulbs
+ " light bulbs will be on in the end out of "
+ numberOfBulbs + " light bulbs");
</script>
|
The previous program is written in O(n*sqrt(n)).
From observation, it is clear that whenever the number of factors is odd, the bulb will be on.
For any non-square number with each divisor, there is a corresponding quotient, so the number of factors will be even.
For every square number, when we divide it by its square root, the quotient will be the same number, i.e. its square root. So it has an odd number of factors.
Therefore, we can write an efficient code for this problem which computes in O(sqrt(n)).
C++
#include<iostream>
#include<math.h>
using namespace std;
int main()
{
int numberOfBulbs = 1000;
int root = sqrt(numberOfBulbs);
for (int i = 1; i < root + 1; i++)
{
cout << "Light bulb " << (i * i)
<< " will be on" << endl;
}
cout << "Total " << root
<< " light bulbs will be on in the end out of "
<< numberOfBulbs << " light bulbs" << endl;
return 0;
}
|
Java
import java.io.*;
class GFG {
public static void main (String[] args) {
int numberOfBulbs = 1000;
int root = (int) Math.sqrt(numberOfBulbs);
for (int i = 1; i < root + 1; i++)
{
System.out.println("Light bulb " + (i * i) +" will be on");
}
System.out.println("Total " + root
+ " light bulbs will be on in the end out of "
+ numberOfBulbs + " light bulbs");
}
}
|
Python3
import math
root = int(math.sqrt(1000))
for i in range(1, root + 1):
print("Light bulb %d will be on"%(i * i))
print(
%root)
|
C#
using System;
using System.Collections.Generic;
class GFG
{
public static void Main(String [] args)
{
int numberOfBulbs = 1000;
int root = (int) Math.Sqrt(numberOfBulbs);
for (int i = 1; i < root + 1; i++)
{
Console.WriteLine("Light bulb " + (i * i) +" will be on");
}
Console.WriteLine("Total " + root
+ " light bulbs will be on in the end out of "
+ numberOfBulbs + " light bulbs");
}
}
|
Javascript
<script>
var numberOfBulbs = 1000;
var root = parseInt( Math.sqrt(numberOfBulbs));
for (i = 1; i < root + 1; i++) {
document.write("Light bulb " + (i * i) + " will be on<br/>");
}
document.write(
"Total " + root + " light bulbs will be on in the end out of "
+ numberOfBulbs + " light bulbs<br/>");
</script>
|
Output:
Light bulb 1 will be on
Light bulb 4 will be on
Light bulb 9 will be on
Light bulb 16 will be on
Light bulb 25 will be on
Light bulb 36 will be on
Light bulb 49 will be on
Light bulb 64 will be on
Light bulb 81 will be on
Light bulb 100 will be on
Light bulb 121 will be on
Light bulb 144 will be on
Light bulb 169 will be on
Light bulb 196 will be on
Light bulb 225 will be on
Light bulb 256 will be on
Light bulb 289 will be on
Light bulb 324 will be on
Light bulb 361 will be on
Light bulb 400 will be on
Light bulb 441 will be on
Light bulb 484 will be on
Light bulb 529 will be on
Light bulb 576 will be on
Light bulb 625 will be on
Light bulb 676 will be on
Light bulb 729 will be on
Light bulb 784 will be on
Light bulb 841 will be on
Light bulb 900 will be on
Light bulb 961 will be on
Total 31 light bulbs will be on in the end out of 1000 light bulbs
Share your thoughts in the comments
Please Login to comment...