Program to find the LCM of two prime numbers
Last Updated :
27 Jun, 2021
Given two prime numbers N and M, the task is to find the Least Common Multiple(LCM) of the two given prime numbers.
Examples:
Input: N = 3, M = 7
Output: 21
Explanation:
The least numbers greater than equals to 3 and 7 which is a multiple of 3 and 7 is 21.
Input: N = 5, M = 5
Output: 5
Explanation:
The least numbers greater than equals to 5 and 5 which is a multiple of 5 and 5 is 5.
Approach: As we know that product of two numbers equals to the product of their Greatest Common Divisor(GCD) and Least Common Multiple(LCM). So, the LCM of the two given prime numbers can be given by: 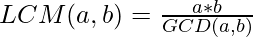 .
.
Since the GCD two different prime numbers are 1, Therefore 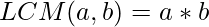 , and if the two given numbers are same then the LCM is the number itself.
, and if the two given numbers are same then the LCM is the number itself.
Below is the implementation of the above approach:
C++
#include <bits/stdc++.h>
using namespace std;
int findLCMPrime(int a, int b)
{
if (a == b) {
return a;
}
return a * b;
}
int main()
{
int a = 3, b = 5;
cout << findLCMPrime(a, b);
return 0;
}
|
Java
class GFG{
static int findLCMPrime(int a, int b)
{
if (a == b)
{
return a;
}
return a * b;
}
public static void main (String[] args)
{
int a = 3, b = 5;
System.out.println(findLCMPrime(a, b));
}
}
|
Python3
def findLCMPrime(a, b):
if (a == b):
return a;
return a * b;
if __name__ == "__main__":
a = 3; b = 5;
print(findLCMPrime(a, b));
|
C#
using System;
class GFG{
static int findLCMPrime(int a, int b)
{
if (a == b)
{
return a;
}
return a * b;
}
public static void Main (string[] args)
{
int a = 3, b = 5;
Console.WriteLine(findLCMPrime(a, b));
}
}
|
Javascript
<script>
function findLCMPrime(a, b)
{
if (a == b)
{
return a;
}
return a * b;
}
let a = 3, b = 5;
document.write(findLCMPrime(a, b));
</script>
|
Time Complexity: O(1)
Auxiliary Space: O(1)
Share your thoughts in the comments
Please Login to comment...