Program for Method Of False Position
Given a function f(x) on floating number x and two numbers ‘a’ and ‘b’ such that f(a)*f(b) < 0 and f(x) is continuous in [a, b]. Here f(x) represents algebraic or transcendental equation. Find root of function in interval [a, b] (Or find a value of x such that f(x) is 0).
Input: A function of x, for example x3 – x2 + 2.
And two values: a = -200 and b = 300 such that
f(a)*f(b) < 0, i.e., f(a) and f(b) have
opposite signs.
Output: The value of root is : -1.00
OR any other value close to root.We strongly recommend to refer below post as a prerequisite of this post.
Solution of Algebraic and Transcendental Equations | Set 1 (The Bisection Method)
In this post The Method Of False Position is discussed. This method is also known as Regula Falsi or The Method of Chords.
Similarities with Bisection Method:
- Same Assumptions: This method also assumes that function is continuous in [a, b] and given two numbers ‘a’ and ‘b’ are such that f(a) * f(b) < 0.
- Always Converges: like Bisection, it always converges, usually considerably faster than Bisection–but sometimes very much more slowly than Bisection.
Differences with Bisection Method:
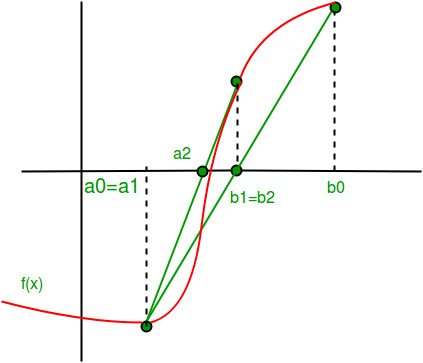
It differs in the fact that we make a chord joining the two points [a, f(a)] and [b, f(b)]. We consider the point at which the chord touches the x axis and named it as c.
Steps:
- Write equation of the line connecting the two points.
y – f(a) = ( (f(b)-f(a))/(b-a) )*(x-a) Now we have to find the point which touches x axis. For that we put y = 0. so x = a - (f(a)/(f(b)-f(a))) * (b-a) x = (a*f(b) - b*f(a)) / (f(b)-f(a)) This will be our c that is c = x.
- If f(c) == 0, then c is the root of the solution.
- Else f(c) != 0
- If value f(a)*f(c) < 0 then root lies between a and c. So we recur for a and c
- Else If f(b)*f(c) < 0 then root lies between b and c. So we recur b and c.
- Else given function doesn’t follow one of assumptions.
Since root may be a floating point number and may converge very slow in worst case, we iterate for a very large number of times such that the answer becomes closer to the root.
Following is the implementation.
C++
// C++ program for implementation of Bisection Method for// solving equations#include<bits/stdc++.h>using namespace std;#define MAX_ITER 1000000// An example function whose solution is determined using// Bisection Method. The function is x^3 - x^2 + 2double func(double x){ return x*x*x - x*x + 2;}// Prints root of func(x) in interval [a, b]void regulaFalsi(double a, double b){ if (func(a) * func(b) >= 0) { cout << "You have not assumed right a and b\n"; return; } double c = a; // Initialize result for (int i=0; i < MAX_ITER; i++) { // Find the point that touches x axis c = (a*func(b) - b*func(a))/ (func(b) - func(a)); // Check if the above found point is root if (func(c)==0) break; // Decide the side to repeat the steps else if (func(c)*func(a) < 0) b = c; else a = c; } cout << "The value of root is : " << c;}// Driver program to test above functionint main(){ // Initial values assumed double a =-200, b = 300; regulaFalsi(a, b); return 0;} |
Java
// java program for implementation// of Bisection Method for// solving equationsimport java.io.*;class GFG { static int MAX_ITER = 1000000; // An example function whose // solution is determined using // Bisection Method. The function // is x^3 - x^2 + 2 static double func(double x) { return (x * x * x - x * x + 2); } // Prints root of func(x) // in interval [a, b] static void regulaFalsi(double a, double b) { if (func(a) * func(b) >= 0) { System.out.println("You have not assumed right a and b"); } // Initialize result double c = a; for (int i = 0; i < MAX_ITER; i++) { // Find the point that touches x axis c = (a * func(b) - b * func(a)) / (func(b) - func(a)); // Check if the above found point is root if (func(c) == 0) break; // Decide the side to repeat the steps else if (func(c) * func(a) < 0) b = c; else a = c; } System.out.println("The value of root is : " + (int)c); } // Driver program public static void main(String[] args) { // Initial values assumed double a = -200, b = 300; regulaFalsi(a, b); }}// This article is contributed by vt_m |
Python3
# Python3 implementation of Bisection# Method for solving equationsMAX_ITER = 1000000# An example function whose solution# is determined using Bisection Method.# The function is x^3 - x^2 + 2def func( x ): return (x * x * x - x * x + 2)# Prints root of func(x) in interval [a, b]def regulaFalsi( a , b): if func(a) * func(b) >= 0: print("You have not assumed right a and b") return -1 c = a # Initialize result for i in range(MAX_ITER): # Find the point that touches x axis c = (a * func(b) - b * func(a))/ (func(b) - func(a)) # Check if the above found point is root if func(c) == 0: break # Decide the side to repeat the steps elif func(c) * func(a) < 0: b = c else: a = c print("The value of root is : " , '%.4f' %c)# Driver code to test above function# Initial values assumeda =-200b = 300regulaFalsi(a, b)# This code is contributed by "Sharad_Bhardwaj". |
C#
// C# program for implementation// of Bisection Method for// solving equationsusing System;class GFG { static int MAX_ITER = 1000000; // An example function whose // solution is determined using // Bisection Method. The function // is x^3 - x^2 + 2 static double func(double x) { return (x * x * x - x * x + 2); } // Prints root of func(x) // in interval [a, b] static void regulaFalsi(double a, double b) { if (func(a) * func(b) >= 0) { Console.WriteLine("You have not assumed right a and b"); } // Initialize result double c = a; for (int i = 0; i < MAX_ITER; i++) { // Find the point that touches x axis c = (a * func(b) - b * func(a)) / (func(b) - func(a)); // Check if the above found point is root if (func(c) == 0) break; // Decide the side to repeat the steps else if (func(c) * func(a) < 0) b = c; else a = c; } Console.WriteLine("The value of root is : " + (int)c); } // Driver program public static void Main(String []args) { // Initial values assumed double a = -200, b = 300; regulaFalsi(a, b); }}// This code is contributed by Sam007. |
Javascript
<script>// JavaScript program for implementation of Bisection Method for// solving equations let MAX_ITER = 1000000 // An example function whose solution is determined using // Bisection Method. The function is x^3 - x^2 + 2 function func(x){ return x*x*x - x*x + 2; } // Prints root of func(x) in interval [a, b] function regulaFalsi( a, b){ if (func(a) * func(b) >= 0){ document.write("You have not assumed right a and b\n"); return; }// Initialize result let c = a; for (let i=0; i < MAX_ITER; i++) { // Find the point that touches x axis c = Math.floor((a*func(b) - b*func(a))/ (func(b) - func(a))); // Check if the above found point is root if (func(c)==0){ break; } // Decide the side to repeat the steps else if (func(c)*func(a) < 0){ b = c; } else{ a = c; } } document.write("The value of root is : " + c); } // Driver program to test above function // Initial values assumed let a =-200; let b = 300; regulaFalsi(a, b); </script> |
Output:
The value of root is : -1
This method always converges, usually considerably faster than Bisection. But worst case can be very slow.
We will soon be discussing other methods to solve algebraic and transcendental equations.
References:
Introductory Methods of Numerical Analysis by S.S. Sastry
https://en.wikipedia.org/wiki/False_position_method
This article is contributed by Abhiraj Smit. Please write comments if you find anything incorrect, or you want to share more information about the topic discussed above
