Printing triangle star pattern using a single loop

Given a number N, the task is to print the star pattern in single loop.

Examples:

Input: N = 9
Output:                    
          * 
         * * 
        * * * 
       * * * * 
      * * * * * 
     * * * * * * 
    * * * * * * * 
   * * * * * * * * 
  * * * * * * * * * 

Input: N = 5
Output:
     * 
    * * 
   * * * 
  * * * * 
 * * * * * 

Please Refer article for printing the pattern in two loops as:
Triangle pattern in Java

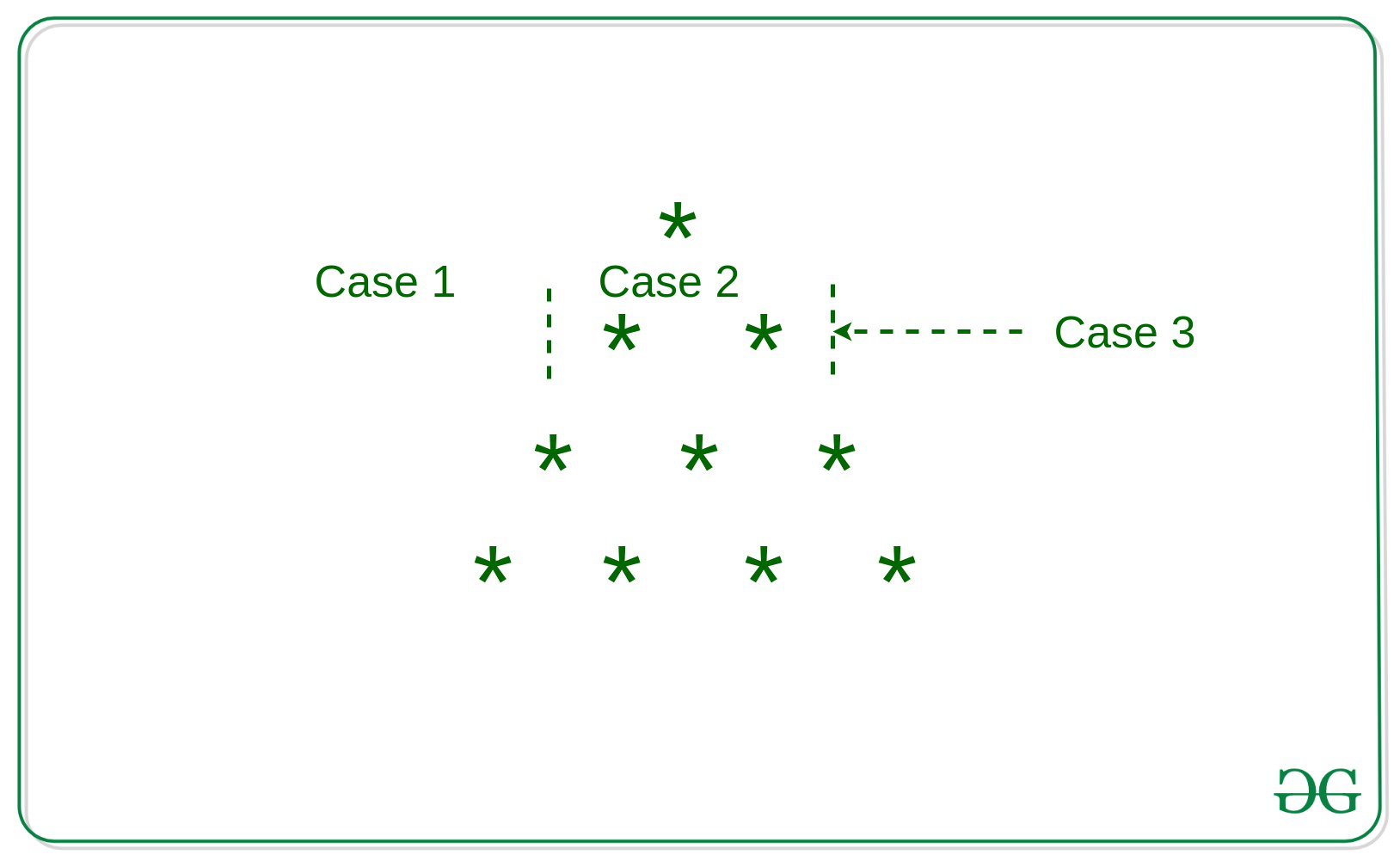
Approach: The idea is to break a column into three parts and solve each part independently of the others.

• Case 1: Spaces before the first *, which takes care of printing white spaces.
• Case 2: Starting of the first * and the ending of the last * in the row, which takes care of printing alternating white spaces and *.
• Case 3: The ending star essentially tells to print a new line or end the program if we have already finished n rows.
  Refer to the image below

Below is the implementation of the above approach:

C++

// C++ implementation of printing
// star pattern in single loop

#include <iostream>
using namespace std;

// Function to print the star
// pattern in single loop
void pattern(int n)
{
    int i, k, flag = 1;

    // Loop to handle number of rows and
    // columns in this case
    for (i = 1, k = 0; i <= 2 * n - 1; i++) {
        // Handles case 1
        if (i < n - k)
            cout << " ";

        // Handles case 2
        else {
            if (flag)
                cout << "*";
            else
                cout << " ";

            flag = 1 - flag;
        }

        // Condition to check case 3
        if (i == n + k) {
            k++;
            cout << endl;

            // Since for nth row we have
            // 2 * n- 1 columns
            if (i == 2 * n - 1)
                break;

            // Reinitializing i as 0,
            // for next row
            i = 0;
            flag = 1;
        }
    }
}

// Driver Code
int main()
{
    int n = 6;

    // Function Call
    pattern(n);
    return 0;
}

Java

// Java implementation of printing
// star pattern in single loop
import java.util.*;

class GFG{

// Function to print the star
// pattern in single loop
static void pattern(int n)
{
    int i, k, flag = 1;

    // Loop to handle number of rows and
    // columns in this case
    for(i = 1, k = 0; i <= 2 * n - 1; i++)
    {

        // Handles case 1
        if (i < n - k)
            System.out.print(" ");

        // Handles case 2
        else
        {
            if (flag == 1)
                System.out.print("*");
            else
                System.out.print(" ");

            flag = 1 - flag;
        }

        // Condition to check case 3
        if (i == n + k)
        {
            k++;
            System.out.println();

            // Since for nth row we have
            // 2 * n- 1 columns
            if (i == 2 * n - 1)
                break;

            // Reinitializing i as 0,
            // for next row
            i = 0;
            flag = 1;
        }
    }
}

// Driver code
public static void main(String[] args)
{
    int n = 6;

    // Function Call
    pattern(n);
}
}

// This code is contributed by offbeat

Python3

# Python3 implementation of
# printing star pattern in
# single loop

# Function to print the star
# pattern in single loop
def pattern(n):

    flag = 1

    # Loop to handle number
    # of rows and columns
    # in this case
    i = 1
    k = 0
    while i <= 2 * n - 1:

        # Handles case 1
        if (i < n - k):
            print(" ", end = "")

        # Handles case 2
        else:
            if (flag):
                print("*", end = "")
            else:
                print(" ", end = "")

            flag = 1 - flag

        # Condition to check case 3
        if (i == n + k):
            k += 1
            print()

            # Since for nth row we
            # have 2 * n- 1 columns
            if (i == 2 * n - 1):
                break

            # Reinitializing i as 0,
            # for next row
            i = 0
            flag = 1

        i += 1

# Driver Code
if __name__ == "__main__":

    n = 6

    # Function Call
    pattern(n)

# This code is contributed by Chitranayal

C#

// C# implementation of printing
// star pattern in single loop
using System;

class GFG{

// Function to print the star
// pattern in single loop
static void pattern(int n)
{
    int i, k, flag = 1;

    // Loop to handle number of rows and
    // columns in this case
    for(i = 1, k = 0; i <= 2 * n - 1; i++)
    {

        // Handles case 1
        if (i < n - k)
            Console.Write(" ");

        // Handles case 2
        else
        {
            if (flag == 1)
                Console.Write("*");
            else
                Console.Write(" ");

            flag = 1 - flag;
        }

        // Condition to check case 3
        if (i == n + k)
        {
            k++;
            Console.WriteLine();

            // Since for nth row we have
            // 2 * n- 1 columns
            if (i == 2 * n - 1)
                break;

            // Reinitializing i as 0,
            // for next row
            i = 0;
            flag = 1;
        }
    }
}

// Driver code
public static void Main()
{
    int n = 6;

    // Function call
    pattern(n);
}
}

// This code is contributed by sanjoy_62

Javascript

<script>

      // JavaScript implementation of printing
      // star pattern in single loop

      // Function to print the star
      // pattern in single loop
      function pattern(n) {
        var i,
          k,
          flag = 1;

        // Loop to handle number of rows and
        // columns in this case
        for (i = 1, k = 0; i <= 2 * n - 1; i++)
        {
          // Handles case 1
          if (i < n - k)
          document.write("  ");
          // Handles case 2
          else {
            if (flag)
            document.write("*");
            else
            document.write("  ");

            flag = 1 - flag;
          }

          // Condition to check case 3
          if (i == n + k) {
            k++;
            document.write("<br>");

            // Since for nth row we have
            // 2 * n- 1 columns
            if (i == 2 * n - 1) break;

            // Reinitializing i as 0,
            // for next row
            i = 0;
            flag = 1;
          }
        }
      }

      // Driver Code
      var n = 6;

      // Function Call
      pattern(n);

</script>

Output

     *
    * *
   * * *
  * * * *
 * * * * *
* * * * * *

Time complexity: O(n^2) for given n
Auxiliary space: O(1)