Print N numbers such that their sum is a Perfect Cube

Given a number N, the task is to find the N numbers such that their sum is a perfect cube.

Examples:

Input: N = 3 
Output: 1 7 19 
Explanation:
Sum of numbers = 1 + 7 + 19 = 27, 
which is the perfect cube of 3 => 3³ = 27

Input: N = 4 
Output: 1 7 19 37 
Sum of numbers = 1 + 7 + 19 + 37 = 64, 
which is the perfect cube of 4 => 4³ = 64 

Approach:
Upon considering Centered Hexagonal Numbers which states that: 

The sum of first N Centered Hexagonal Numbers is a perfect cube of N

So from Centered Hexagonal Numbers, the first N terms of the series will give the N numbers such that their sum is a perfect cube.

For example:

For N = 1,
    Centered Hexagonal Series = 1
    and 13 = 1
    Hence, {1} is the required N number

For N = 2,
    Centered Hexagonal Series = 1, 7
    and 23 = 1 + 7 = 8
    Hence, {1, 7} are the required N number

For N = 3,
    Centered Hexagonal Series = 1, 7, 19
    and 33 = 1 + 7 + 19 = 27
    Hence, {1, 7, 19} are the required N number
.
.
and so on.

Therefore it can be said that printing the first N terms of the Centered Hexagonal Numbers will give the required N numbers.
Also, the Nth term of the Centered Hexagonal Numbers is: 

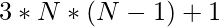
Algorithm:

• Iterate a loop with a loop variable (say i) from 1 to N and for each of the iteration – 
  
  1. Find the N^th term of the centered hexagonal number using the formulae 3*i*(i-1) + 1.
  2. Append the i^th term in an array.

Below is the implementation of the above approach: 

C++

// C++ implementation to find the N
// numbers such that their
// sum is a perfect cube

#include <bits/stdc++.h>
using namespace std;

// Function to find the N
// numbers such that their
// sum is a perfect cube
void findNumbers(int n)
{
    int i = 1;
    // Loop to find the Ith term
    // of the Centered Hexagonal number
    while (i <= n) {
        cout << (3 * i * (i - 1) + 1)
             << " ";
        i++;
    }
}

// Driver Code
int main()
{
    int n = 4;

    // Function Call
    findNumbers(n);
}

Java

// Java implementation to find the N
// numbers such that their
// sum is a perfect cube
import java.io.*;
public class GFG
{

    // Function to find the N
    // numbers such that their
    // sum is a perfect cube
    static void findNumbers(int n)
    {
        int i = 1;

        // Loop to find the Ith term
        // of the Centered Hexagonal number
        while (i <= n)
        {
            System.out.print((3 * i * (i - 1) + 1) + " ");
            i++;
        }
    }

    // Driver Code
    public static void main (String[] args)
    {
        int n = 4;

        // Function Call
        findNumbers(n);
    }
}

// This code is contributed by AnkitRai01

C#

// C# implementation to find the N
// numbers such that their
// sum is a perfect cube
using System;

public class GFG
{

    // Function to find the N
    // numbers such that their
    // sum is a perfect cube
    static void findNumbers(int n)
    {
        int i = 1;

        // Loop to find the Ith term
        // of the Centered Hexagonal number
        while (i <= n)
        {
            Console.Write((3 * i * (i - 1) + 1) + " ");
            i++;
        }
    }

    // Driver Code
    public static void Main()
    {
        int n = 4;

        // Function Call
        findNumbers(n);
    }
}

// This code is contributed by AnkitRai01

Python3

# Python3 implementation to find the N
# numbers such that their
# sum is a perfect cube

# Function to find the N
# numbers such that their
# sum is a perfect cube
def findNumbers(n):
    i = 1

    # Loop to find the Ith term
    # of the Centered Hexagonal number
    while (i <= n):
        print((3 * i * (i - 1) + 1), end=" ")
        i += 1

# Driver Code
n = 4

# Function Call
findNumbers(n)

# This code is contributed by mohit kumar 29

Javascript

<script>

// Javascript implementation to find
// the N numbers such that their sum
// is a perfect cube

// Function to find the N
// numbers such that their
// sum is a perfect cube
function findNumbers(n)
{
    let i = 1;

    // Loop to find the Ith term
    // of the Centered Hexagonal number
    while (i <= n)
    {
        document.write((3 * i * (i - 1) +
                       1) + " ");
        i++;
    }
}

// Driver Code
let n = 4;

// Function Call
findNumbers(n);

// This code is contributed by Surbhi Tyagi.

</script>

Output:

1 7 19 37

Performance Analysis:

• Time Complexity: As in the above approach, we are finding all the N Centered hexagonal numbers, So it will take O(N).
• Auxiliary Space: As in the above approach, there are no extra space used, So the Auxiliary Space used will be O(1)