Permutation of numbers such that sum of two consecutive numbers is a perfect square

Prerequisite: Hamiltonian Cycle Given an integer n(>=2), find a permutation of numbers from 1 to n such that the sum of two consecutive numbers of that permutation is a perfect square. If that kind of permutation is not possible to print “No Solution”.

Examples:

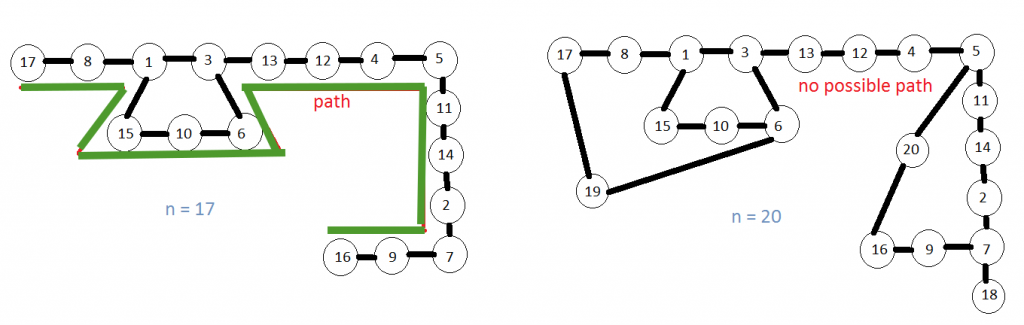
Input : 17
Output : [16, 9, 7, 2, 14, 11, 5, 4, 12, 13, 3, 6, 10, 15, 1, 8, 17]
Explanation : 16+9 = 25 = 5*5, 9+7 = 16 = 4*4, 7+2 = 9 = 3*3 and so on.

Input: 20
Output: No Solution

Input : 25
Output : [2, 23, 13, 12, 24, 25, 11, 14, 22, 3, 1, 8,  
          17, 19, 6, 10, 15, 21, 4, 5, 20, 16, 9, 7, 18]

Method: We can represent a graph, where numbers from 1 to n are the nodes of the graph and there is an edge between ith and jth node if (i+j) is a perfect square. Then we can search if there is any Hamiltonian Path in the graph. If there is at least one path then we print a path otherwise we print “No Solution”. 

Approach:

1. First list up all the perfect square numbers 
   which we can get by adding two numbers.
   We can get at max (2*n-1). so we will take 
   only the squares up to (2*n-1).
2. Take an adjacency matrix to represent the graph.
3. For each number from 1 to n find out numbers with 
   which it can add upto a perfect square number.
   Fill respective cells of the adjacency matrix by 1.
4. Now find if there is any Hamiltonian path in the 
   graph using backtracking as discussed earlier.  

Implementation:

C++

#include <bits/stdc++.h>
using namespace std;

// Function to check if a node is safe to visit in the
// current Hamiltonian path
bool issafe(int v, int graph[][20], int path[], int pos)
{
    // Check if the current node is connected to the
    // previous node in the path
    if (graph[path[pos - 1]][v] == 0)
        return false;

    // Check if the current node has already been visited in
    // the current path
    for (int i = 0; i < pos; i++)
        if (path[i] == v)
            return false;

    // If the current node is connected to the previous node
    // and has not been visited yet, return true
    return true;
}

// Function to form the Hamiltonian path by visiting nodes
// recursively
bool formpath(int graph[][20], int path[], int pos, int n)
{
    // If all the nodes have been visited, return true
    if (pos == n + 1)
        return true;

    // Try visiting each node and see if it forms a
    // Hamiltonian path
    for (int v = 1; v < n + 1; v++) {
        if (issafe(v, graph, path, pos)) {
            path[pos] = v;
            if (formpath(graph, path, pos + 1, n) == true)
                return true;
            path[pos] = -1;
        }
    }
    // If none of the nodes form a Hamiltonian path, return
    // false
    return false;
}

// Function to find a Hamiltonian path in a given graph
void hampath(int n)
{
    // Adjacency matrix to store the graph
    int graph[20][20];
    // Array to store the Hamiltonian path
    int path[20];
    // Temporary variable used to store square root of 2n-1
    int k = 0;

    // If there is only 1 node in the graph, there is no
    // Hamiltonian path
    if (n == 1) {
        cout << "No Solution";
        return;
    }

    // Vector to store the squares of the numbers from 1 to
    // sqrt(2n-1)
    vector<int> l;
    int nsqrt = sqrt(2 * n - 1);
    for (int i = 1; i <= nsqrt + 1; i++) {
        l.push_back(i * i);
    }

    // Initialize the graph to 0
    memset(graph, 0, sizeof(graph));

    // Form the graph using the squares stored in the vector
    // 'l'
    for (int i = 1; i < n + 1; i++) {
        for (auto ele : l) {
            // Check if the difference between the square
            // and the current node is greater than 0 and
            // less than or equal to n Also, make sure that
            // the difference is not equal to 2 times the
            // current node (to avoid repeated edges)
            if ((ele - i) > 0 && (ele - i) <= n
                && (2 * i != ele)) {
                graph[i][ele - i] = 1;
                graph[ele - i][i] = 1;
            }
        }
    }

    // Loop through all vertices starting from vertex 1
    for (int j = 1; j < n + 1; j++) {
        // Reset the path array
        memset(path, -1, sizeof(path));
        // Start the path from vertex j
        path[1] = j;
        // Check if a Hamiltonian path can be formed
        // starting from vertex j
        if (formpath(graph, path, 2, n) == true) {
            cout << "Hamiltonian Path: ";
            // Print the path
            for (int i = 1; i < n + 1; i++) {
                cout << path[i] << " ";
            }
            // Return the path
            return;
        }
    }

    // If no solution is found, print "No Solution"
    cout << "No Solution";
    return;
}
// Driver Function
    int main()
    {
        cout << "17 -> ";
        hampath(17);
        cout << endl << "20 -> ";
        hampath(20);
        cout << endl << "25 -> ";
        hampath(25);
        return 0;
    }

Java

import java.util.*;

public class HamiltonianPath {

    // Function to check if a node is safe to visit in the
    // current Hamiltonian path
    static boolean issafe(int v, int[][] graph, int[] path,
                          int pos)
    {
        // Check if the current node is connected to the
        // previous node in the path
        if (graph[path[pos - 1]][v] == 0) {
            return false;
        }

        // Check if the current node has already been
        // visited in the current path
        for (int i = 0; i < pos; i++) {
            if (path[i] == v) {
                return false;
            }
        }

        // If the current node is connected to the previous
        // node and has not been visited yet, return true
        return true;
    }

    // Function to form the Hamiltonian path by visiting
    // nodes recursively
    static boolean formpath(int[][] graph, int[] path,
                            int pos, int n)
    {
        // If all the nodes have been visited, return true
        if (pos == n + 1) {
            return true;
        }

        // Try visiting each node and see if it forms a
        // Hamiltonian path
        for (int v = 1; v < n + 1; v++) {
            if (issafe(v, graph, path, pos)) {
                path[pos] = v;
                if (formpath(graph, path, pos + 1, n)
                    == true) {
                    return true;
                }
                path[pos] = -1;
            }
        }
        // If none of the nodes form a Hamiltonian path,
        // return false
        return false;
    }

    // Function to find a Hamiltonian path in a given graph
    static void hampath(int n)
    {
        // Adjacency matrix to store the graph
        int[][] graph = new int[n+1][n+1];
        // Array to store the Hamiltonian path
        int[] path = new int[n+1];

        // If there is only 1 node in the graph, there is no
        // Hamiltonian path
        if (n == 1) {
            System.out.println("No Solution");
            return;
        }

        // Vector to store the squares of the numbers from 1
        // to sqrt(2n-1)
        ArrayList<Integer> l = new ArrayList<Integer>();
        int nsqrt = (int)Math.sqrt(2 * n - 1);
        for (int i = 1; i <= nsqrt + 1; i++) {
            l.add(i * i);
        }

        // Initialize the graph to 0
        for (int i = 1; i < n + 1; i++) {
            for (int j = 1; j < n + 1; j++) {
                graph[i][j] = 0;
            }
        }

        // Form the graph using the squares stored in the
        // vector 'l'
        for (int i = 1; i < n + 1; i++) {
            for (int ele : l) {
                // Check if the difference between the
                // square and the current node is greater
                // than 0 and less than or equal to n Also,
                // make sure that the difference is not
                // equal to 2 times the current node (to
                // avoid repeated edges)
                if ((ele - i) > 0 && (ele - i) <= n
                    && (2 * i != ele)) {
                    graph[i][ele - i] = 1;
                    graph[ele - i][i] = 1;
                }
            }
        }

        for (int j = 1; j < n + 1; j++) {
            // Reset the path array
            Arrays.fill(path, -1);
            // Start the path from vertex j
            path[1] = j;
            // Check if a Hamiltonian path can be formed
            // starting from vertex j
            if (formpath(graph, path, 2, n) == true) {
                System.out.print("Hamiltonian Path: ");
                // Print the path
                for (int i = 1; i < n + 1; i++) {
                    System.out.print(path[i] + " ");
                }
                // Return the path
                return;
            }
        }
        // If no solution is found, print "No Solution"
        System.out.print("No Solution");
    }
    public static void main(String[] args)
    {
        System.out.print("17 -> ");
        hampath(17);
        System.out.println();
        System.out.print("20 -> ");
        hampath(20);
        System.out.println();
        System.out.print("25 -> ");
        hampath(25);
    }
}

Python3

# Python3 program for Sum-square series using
# hamiltonian path concept and backtracking

# Function to check whether we can add number
# v with the path in the position pos.


def issafe(v, graph, path, pos):

    # if there is no edge between v and the
    # last element of the path formed so far
    # return false.
    if (graph[path[pos - 1]][v] == 0):
        return False

    # Otherwise if there is an edge between
    # v and last element of the path formed so
    # far, then check all the elements of the
    # path. If v is already in the path return
    # false.
    for i in range(pos):

        if (path[i] == v):
            return False

    # If none of the previous cases satisfies
    # then we can add v to the path in the
    # position pos. Hence return true.
    return True

# Function to form a path based on the graph.


def formpath(graph, path, pos):

    # If all the elements are included in the
    # path i.e. length of the path is n then
    # return true i.e. path formed.
    n = len(graph) - 1
    if (pos == n + 1):
        return True

    # This loop checks for each element if it
    # can be fitted as the next element of the
    # path and recursively finds the next
    # element of the path.
    for v in range(1, n + 1):

        if issafe(v, graph, path, pos):
            path[pos] = v

            # Recurs for next element of the path.
            if (formpath(graph, path, pos + 1) == True):
                return True

            # If adding v does not give a solution
            # then remove it from path
            path[pos] = -1

    # if any vertex cannot be added with the
    # formed path then return false and
    # backtracks.
    return False

# Function to find out sum-square series.


def hampath(n):

    # base case: if n = 1 there is no solution
    if n == 1:
        return 'No Solution'

    # Make an array of perfect squares from 1
    # to (2 * n-1)
    l = list()

    for i in range(1, int((2 * n-1) ** 0.5) + 1):
        l.append(i**2)

    # Form the graph where sum of two adjacent
    # vertices is a perfect square
    graph = [[0 for i in range(n + 1)] for j in range(n + 1)]

    for i in range(1, n + 1):
        for ele in l:

            if ((ele-i) > 0 and (ele-i) <= n
                    and (2 * i != ele)):
                graph[i][ele - i] = 1
                graph[ele - i][i] = 1

    # starting from 1 upto n check for each
    # element i if any path can be formed
    # after taking i as the first element.
    for j in range(1, n + 1):
        path = [-1 for k in range(n + 1)]
        path[1] = j

        # If starting from j we can form any path
        # then we will return the path
        if formpath(graph, path, 2) == True:
            return path[1:]

    # If no path can be formed at all return
    # no solution.
    return 'No Solution'


# Driver Function
print(17, '->', hampath(17))
print(20, '->', hampath(20))
print(25, '->', hampath(25))

C#

//C# Equivalent of above code
using System;
using System.Collections.Generic;

public class HamiltonianPath
{
  // Function to check if a node is safe to visit in the
  // current Hamiltonian path
  static bool issafe(int v, int[,] graph, int[] path,
                     int pos)
  {

    // Check if the current node is connected to the
    // previous node in the path
    if (graph[path[pos - 1], v] == 0)
    {
      return false;
    }

    // Check if the current node has already been
    // visited in the current path
    for (int i = 0; i < pos; i++)
    {
      if (path[i] == v)
      {
        return false;
      }
    }

    // If the current node is connected to the previous
    // node and has not been visited yet, return true
    return true;
  }

  // Function to form the Hamiltonian path by visiting
  // nodes recursively
  static bool formpath(int[,] graph, int[] path,
                       int pos, int n)
  {
    // If all the nodes have been visited, return true
    if (pos == n + 1)
    {
      return true;
    }

    // Try visiting each node and see if it forms a
    // Hamiltonian path
    for (int v = 1; v < n + 1; v++)
    {
      if (issafe(v, graph, path, pos))
      {
        path[pos] = v;
        if (formpath(graph, path, pos + 1, n)
            == true)
        {
          return true;
        }
        path[pos] = -1;
      }
    }

    // If none of the nodes form a Hamiltonian path,
    // return false
    return false;
  }

  // Function to find a Hamiltonian path in a given graph
  static void hampath(int n)
  {

    // Adjacency matrix to store the graph
    int[,] graph = new int[n + 1, n + 1];

    // Array to store the Hamiltonian path
    int[] path = new int[n + 1];

    // If there is only 1 node in the graph, there is no
    // Hamiltonian path
    if (n == 1)
    {
      Console.WriteLine("No Solution");
      return;
    }

    // List to store the squares of the numbers from 1
    // to sqrt(2n-1)
    List<int> l = new List<int>();
    int nsqrt = (int)Math.Sqrt(2 * n - 1);
    for (int i = 1; i <= nsqrt + 1; i++)
    {
      l.Add(i * i);
    }

    // Initialize the graph to 0
    for (int i = 1; i < n + 1; i++)
    {
      for (int j = 1; j < n + 1; j++)
      {
        graph[i, j] = 0;
      }
    }

    // Form the graph using the squares stored in the
    // List 'l'
    for (int i = 1; i < n + 1; i++)
    {
      foreach (int ele in l)
      {
        // Check if the difference between the
        // square and the current node is greater
        // than 0 and less than or equal to n Also,
        // make sure that the difference is not
        // equal to 2 times the current node (to
        // avoid repeated edges)
        if ((ele - i) > 0 && (ele - i) <= n
            && (2 * i != ele))
        {
          graph[i, ele - i] = 1;
          graph[ele - i, i] = 1;
        }
      }
    }

    for (int j = 1; j < n + 1; j++)
    {
      // Reset the path array
      Array.Fill(path, -1);
      // Start the path from vertex j
      path[1] = j;

      // Check if a Hamiltonian path can be formed
      // starting from vertex j
      if (formpath(graph, path, 2, n) == true)
      {
        Console.Write("Hamiltonian Path: ");
        // Print the path
        for (int i = 1; i < n + 1; i++)
        {
          Console.Write(path[i] + " ");
        }
        // Return the path
        return;
      }
    }

    // If no solution is found, print "No Solution"
    Console.Write("No Solution");
  }
  public static void Main(string[] args)
  {
    Console.Write("17 -> ");
    hampath(17);
    Console.WriteLine();
    Console.Write("20 -> ");
    hampath(20);
    Console.WriteLine();
    Console.Write("25 -> ");
    hampath(25);
  }
}

Javascript

function issafe(v, graph, path, pos) {
    if (graph[path[pos - 1]][v] === 0) {
        return false;
    }
    for (let i = 0; i < pos; i++) {
        if (path[i] === v) {
            return false;
        }
    }
    return true;
}

function formpath(graph, path, pos, n) {
    if (pos === n + 1) {
        return true;
    }
    for (let v = 1; v < n + 1; v++) {
        if (issafe(v, graph, path, pos)) {
            path[pos] = v;
            if (formpath(graph, path, pos + 1, n)) {
                return true;
            }
            path[pos] = -1;
        }
    }
    return false;
}

function hampath(n) {
    const graph = new Array(n + 1).fill(0).map(() => new Array(n + 1).fill(0));
    const path = new Array(n + 1).fill(-1);
    if (n === 1) {
        console.log("No Solution");
        return;
    }
    const l = [];
    const nsqrt = Math.floor(Math.sqrt(2 * n - 1));
    for (let i = 1; i <= nsqrt + 1; i++) {
        l.push(i * i);
    }
    for (let i = 1; i < n + 1; i++) {
        for (let j = 1; j < n + 1; j++) {
            graph[i][j] = 0;
        }
    }
    for (let i = 1; i < n + 1; i++) {
        for (let ele of l) {
            if ((ele - i) > 0 && (ele - i) <= n && (2 * i !== ele)) {
                graph[i][ele - i] = 1;
                graph[ele - i][i] = 1;
            }
        }
    }

    for (let j = 1; j < n + 1; j++) {
        path[1] = j;
        if (formpath(graph, path, 2, n)) {
            console.log("Hamiltonian Path: " + path.slice(1).join(" "));
            return;
        }
    }
    console.log("No Solution");
}

console.log("17 -> ");
hampath(17);
console.log();
console.log("20 -> ");
hampath(20);
console.log();
console.log("25 -> ");
hampath(25);

Output

17 -> [16, 9, 7, 2, 14, 11, 5, 4, 12, 13, 3, 6, 10, 15, 1, 8, 17]
20 -> No Solution
25 -> [2, 23, 13, 12, 24, 25, 11, 14, 22, 3, 1, 8, 17, 19, 6, 10, 15, 21, 4, 5, 20, 16, 9, 7, 18]

Discussion:

• This backtracking algorithm takes exponential time to find Hamiltonian Path. 
• Hence the time complexity of this algorithm is exponential. In the last part of the hampath(n) function if we just print the path rather returning it then it will print all possible Hamiltonian Path i.e. all possible representations. Actually we will first get a representation like this for n = 15. For n<15 there is no representation. 
• For n = 18, 19, 20, 21, 22, 24 there is also no Hamiltonian Path. For rest of the numbers it works well.