Input: graph[][] = {{0, 1, 1, 0, 0, 1}, {1, 0, 1, 0, 1, 1}, {1, 1, 0, 1, 0, 0}, {0, 0, 1, 0, 1, 0}, {0, 1, 0, 1, 0, 1}, {1, 1, 0, 0, 1, 0}}
Output:
0 1 2 3 4 5 0
0 1 5 4 3 2 0
0 2 3 4 1 5 0
0 2 3 4 5 1 0
0 5 1 4 3 2 0
0 5 4 3 2 1 0
Explanation:
All Possible Hamiltonian Cycles for the following graph (with the starting vertex as 0) are
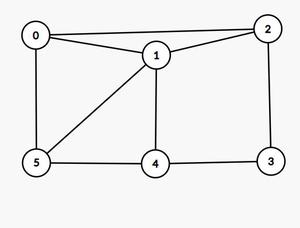
- {0 ? 1 ? 2 ? 3 ? 4 ? 5 ? 0}
- {0 ? 1 ? 5 ? 4 ? 3 ? 2 ? 0}
- {0 ? 2 ? 3 ? 4 ? 1 ? 5 ? 0}
- {0 ? 2 ? 3 ? 4 ? 5 ? 1 ? 0}
- {0 ? 5 ? 1 ? 4 ? 3 ? 2 ? 0}
- {0 ? 5 ? 4 ? 3 ? 2 ? 1 ? 0}
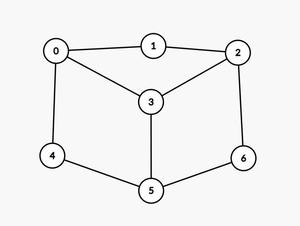
Input: graph[][] = {{0, 1, 0, 1, 1, 0, 0}, {1, 0, 1, 0, 0, 0, 0}, {0, 1, 0, 1, 0, 0, 1}, {1, 0, 1, 0, 0, 1, 0}, {1, 0, 0, 0, 0, 1, 0}, {0, 0, 0, 1, 1, 0, 1}, {0, 0, 1, 0, 0, 1, 0}}
Output: No Hamiltonian Cycle possible
Explanation:
For the given graph, no Hamiltonian Cycle is possible: