Permutation of numbers such that sum of two consecutive numbers is a perfect square
Last Updated :
10 Mar, 2023
Prerequisite: Hamiltonian Cycle Given an integer n(>=2), find a permutation of numbers from 1 to n such that the sum of two consecutive numbers of that permutation is a perfect square. If that kind of permutation is not possible to print “No Solution”.
Examples:
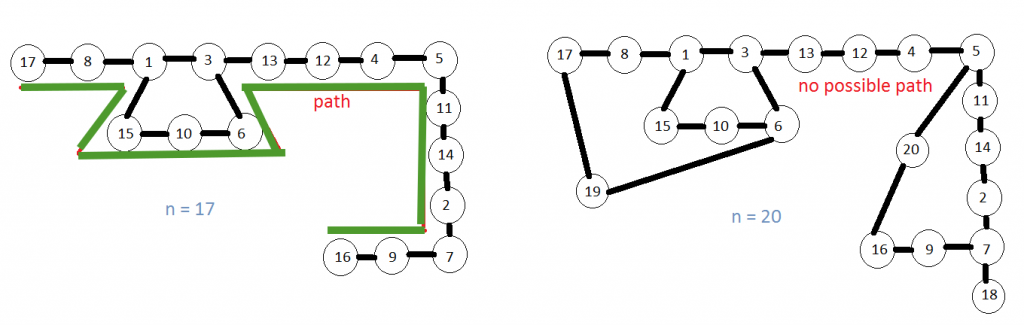
Input : 17
Output : [16, 9, 7, 2, 14, 11, 5, 4, 12, 13, 3, 6, 10, 15, 1, 8, 17]
Explanation : 16+9 = 25 = 5*5, 9+7 = 16 = 4*4, 7+2 = 9 = 3*3 and so on.
Input: 20
Output: No Solution
Input : 25
Output : [2, 23, 13, 12, 24, 25, 11, 14, 22, 3, 1, 8,
17, 19, 6, 10, 15, 21, 4, 5, 20, 16, 9, 7, 18]
Method: We can represent a graph, where numbers from 1 to n are the nodes of the graph and there is an edge between ith and jth node if (i+j) is a perfect square. Then we can search if there is any Hamiltonian Path in the graph. If there is at least one path then we print a path otherwise we print “No Solution”.
Approach:
1. First list up all the perfect square numbers
which we can get by adding two numbers.
We can get at max (2*n-1). so we will take
only the squares up to (2*n-1).
2. Take an adjacency matrix to represent the graph.
3. For each number from 1 to n find out numbers with
which it can add upto a perfect square number.
Fill respective cells of the adjacency matrix by 1.
4. Now find if there is any Hamiltonian path in the
graph using backtracking as discussed earlier.
Implementation:
C++
#include <bits/stdc++.h>
using namespace std;
bool issafe(int v, int graph[][20], int path[], int pos)
{
if (graph[path[pos - 1]][v] == 0)
return false;
for (int i = 0; i < pos; i++)
if (path[i] == v)
return false;
return true;
}
bool formpath(int graph[][20], int path[], int pos, int n)
{
if (pos == n + 1)
return true;
for (int v = 1; v < n + 1; v++) {
if (issafe(v, graph, path, pos)) {
path[pos] = v;
if (formpath(graph, path, pos + 1, n) == true)
return true;
path[pos] = -1;
}
}
return false;
}
void hampath(int n)
{
int graph[20][20];
int path[20];
int k = 0;
if (n == 1) {
cout << "No Solution";
return;
}
vector<int> l;
int nsqrt = sqrt(2 * n - 1);
for (int i = 1; i <= nsqrt + 1; i++) {
l.push_back(i * i);
}
memset(graph, 0, sizeof(graph));
for (int i = 1; i < n + 1; i++) {
for (auto ele : l) {
if ((ele - i) > 0 && (ele - i) <= n
&& (2 * i != ele)) {
graph[i][ele - i] = 1;
graph[ele - i][i] = 1;
}
}
}
for (int j = 1; j < n + 1; j++) {
memset(path, -1, sizeof(path));
path[1] = j;
if (formpath(graph, path, 2, n) == true) {
cout << "Hamiltonian Path: ";
for (int i = 1; i < n + 1; i++) {
cout << path[i] << " ";
}
return;
}
}
cout << "No Solution";
return;
}
int main()
{
cout << "17 -> ";
hampath(17);
cout << endl << "20 -> ";
hampath(20);
cout << endl << "25 -> ";
hampath(25);
return 0;
}
|
Java
import java.util.*;
public class HamiltonianPath {
static boolean issafe(int v, int[][] graph, int[] path,
int pos)
{
if (graph[path[pos - 1]][v] == 0) {
return false;
}
for (int i = 0; i < pos; i++) {
if (path[i] == v) {
return false;
}
}
return true;
}
static boolean formpath(int[][] graph, int[] path,
int pos, int n)
{
if (pos == n + 1) {
return true;
}
for (int v = 1; v < n + 1; v++) {
if (issafe(v, graph, path, pos)) {
path[pos] = v;
if (formpath(graph, path, pos + 1, n)
== true) {
return true;
}
path[pos] = -1;
}
}
return false;
}
static void hampath(int n)
{
int[][] graph = new int[n+1][n+1];
int[] path = new int[n+1];
if (n == 1) {
System.out.println("No Solution");
return;
}
ArrayList<Integer> l = new ArrayList<Integer>();
int nsqrt = (int)Math.sqrt(2 * n - 1);
for (int i = 1; i <= nsqrt + 1; i++) {
l.add(i * i);
}
for (int i = 1; i < n + 1; i++) {
for (int j = 1; j < n + 1; j++) {
graph[i][j] = 0;
}
}
for (int i = 1; i < n + 1; i++) {
for (int ele : l) {
if ((ele - i) > 0 && (ele - i) <= n
&& (2 * i != ele)) {
graph[i][ele - i] = 1;
graph[ele - i][i] = 1;
}
}
}
for (int j = 1; j < n + 1; j++) {
Arrays.fill(path, -1);
path[1] = j;
if (formpath(graph, path, 2, n) == true) {
System.out.print("Hamiltonian Path: ");
for (int i = 1; i < n + 1; i++) {
System.out.print(path[i] + " ");
}
return;
}
}
System.out.print("No Solution");
}
public static void main(String[] args)
{
System.out.print("17 -> ");
hampath(17);
System.out.println();
System.out.print("20 -> ");
hampath(20);
System.out.println();
System.out.print("25 -> ");
hampath(25);
}
}
|
Python3
def issafe(v, graph, path, pos):
if (graph[path[pos - 1]][v] == 0):
return False
for i in range(pos):
if (path[i] == v):
return False
return True
def formpath(graph, path, pos):
n = len(graph) - 1
if (pos == n + 1):
return True
for v in range(1, n + 1):
if issafe(v, graph, path, pos):
path[pos] = v
if (formpath(graph, path, pos + 1) == True):
return True
path[pos] = -1
return False
def hampath(n):
if n == 1:
return 'No Solution'
l = list()
for i in range(1, int((2 * n-1) ** 0.5) + 1):
l.append(i**2)
graph = [[0 for i in range(n + 1)] for j in range(n + 1)]
for i in range(1, n + 1):
for ele in l:
if ((ele-i) > 0 and (ele-i) <= n
and (2 * i != ele)):
graph[i][ele - i] = 1
graph[ele - i][i] = 1
for j in range(1, n + 1):
path = [-1 for k in range(n + 1)]
path[1] = j
if formpath(graph, path, 2) == True:
return path[1:]
return 'No Solution'
print(17, '->', hampath(17))
print(20, '->', hampath(20))
print(25, '->', hampath(25))
|
C#
using System;
using System.Collections.Generic;
public class HamiltonianPath
{
static bool issafe(int v, int[,] graph, int[] path,
int pos)
{
if (graph[path[pos - 1], v] == 0)
{
return false;
}
for (int i = 0; i < pos; i++)
{
if (path[i] == v)
{
return false;
}
}
return true;
}
static bool formpath(int[,] graph, int[] path,
int pos, int n)
{
if (pos == n + 1)
{
return true;
}
for (int v = 1; v < n + 1; v++)
{
if (issafe(v, graph, path, pos))
{
path[pos] = v;
if (formpath(graph, path, pos + 1, n)
== true)
{
return true;
}
path[pos] = -1;
}
}
return false;
}
static void hampath(int n)
{
int[,] graph = new int[n + 1, n + 1];
int[] path = new int[n + 1];
if (n == 1)
{
Console.WriteLine("No Solution");
return;
}
List<int> l = new List<int>();
int nsqrt = (int)Math.Sqrt(2 * n - 1);
for (int i = 1; i <= nsqrt + 1; i++)
{
l.Add(i * i);
}
for (int i = 1; i < n + 1; i++)
{
for (int j = 1; j < n + 1; j++)
{
graph[i, j] = 0;
}
}
for (int i = 1; i < n + 1; i++)
{
foreach (int ele in l)
{
if ((ele - i) > 0 && (ele - i) <= n
&& (2 * i != ele))
{
graph[i, ele - i] = 1;
graph[ele - i, i] = 1;
}
}
}
for (int j = 1; j < n + 1; j++)
{
Array.Fill(path, -1);
path[1] = j;
if (formpath(graph, path, 2, n) == true)
{
Console.Write("Hamiltonian Path: ");
for (int i = 1; i < n + 1; i++)
{
Console.Write(path[i] + " ");
}
return;
}
}
Console.Write("No Solution");
}
public static void Main(string[] args)
{
Console.Write("17 -> ");
hampath(17);
Console.WriteLine();
Console.Write("20 -> ");
hampath(20);
Console.WriteLine();
Console.Write("25 -> ");
hampath(25);
}
}
|
Javascript
function issafe(v, graph, path, pos) {
if (graph[path[pos - 1]][v] === 0) {
return false;
}
for (let i = 0; i < pos; i++) {
if (path[i] === v) {
return false;
}
}
return true;
}
function formpath(graph, path, pos, n) {
if (pos === n + 1) {
return true;
}
for (let v = 1; v < n + 1; v++) {
if (issafe(v, graph, path, pos)) {
path[pos] = v;
if (formpath(graph, path, pos + 1, n)) {
return true;
}
path[pos] = -1;
}
}
return false;
}
function hampath(n) {
const graph = new Array(n + 1).fill(0).map(() => new Array(n + 1).fill(0));
const path = new Array(n + 1).fill(-1);
if (n === 1) {
console.log("No Solution");
return;
}
const l = [];
const nsqrt = Math.floor(Math.sqrt(2 * n - 1));
for (let i = 1; i <= nsqrt + 1; i++) {
l.push(i * i);
}
for (let i = 1; i < n + 1; i++) {
for (let j = 1; j < n + 1; j++) {
graph[i][j] = 0;
}
}
for (let i = 1; i < n + 1; i++) {
for (let ele of l) {
if ((ele - i) > 0 && (ele - i) <= n && (2 * i !== ele)) {
graph[i][ele - i] = 1;
graph[ele - i][i] = 1;
}
}
}
for (let j = 1; j < n + 1; j++) {
path[1] = j;
if (formpath(graph, path, 2, n)) {
console.log("Hamiltonian Path: " + path.slice(1).join(" "));
return;
}
}
console.log("No Solution");
}
console.log("17 -> ");
hampath(17);
console.log();
console.log("20 -> ");
hampath(20);
console.log();
console.log("25 -> ");
hampath(25);
|
Output
17 -> [16, 9, 7, 2, 14, 11, 5, 4, 12, 13, 3, 6, 10, 15, 1, 8, 17]
20 -> No Solution
25 -> [2, 23, 13, 12, 24, 25, 11, 14, 22, 3, 1, 8, 17, 19, 6, 10, 15, 21, 4, 5, 20, 16, 9, 7, 18]
Discussion:
- This backtracking algorithm takes exponential time to find Hamiltonian Path.
- Hence the time complexity of this algorithm is exponential. In the last part of the hampath(n) function if we just print the path rather returning it then it will print all possible Hamiltonian Path i.e. all possible representations. Actually we will first get a representation like this for n = 15. For n<15 there is no representation.
- For n = 18, 19, 20, 21, 22, 24 there is also no Hamiltonian Path. For rest of the numbers it works well.
Like Article
Suggest improvement
Share your thoughts in the comments
Please Login to comment...