Prime Subset Product Problem
Last Updated :
09 Jun, 2023
Given an array arr[] of N integers. The value of a subset of array A is defined as the product of all prime numbers in that subset. If there are no primes in the subset then the value of that subset is 1. The task is to calculate the product of values of all possible non-empty subsets of the given array modulus 100000007.
Examples:
Input: arr[] = {3, 7}
Output: 441
val({3}) = 3
val({7}) = 7
val({3, 7}) = 3 * 7 = 21
3 * 7 * 21 = 441
Input: arr[] = {1, 1, 1}
Output: 1
Approach: Since it is known that a number occurs 2N – 1 times in all the subsets of the given array of size N. So if a number X is prime then the contribution of X will be X * X * X * ….. * 2N – 1 time i.e.
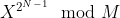
Since 2N – 1 will also be a large number, it cannot be calculated directly. Fermat’s Theorem will be used to calculate the power here.
)&space;}&space;\mod&space;M)
After that, the value of each element can be calculated easily.
Below is the implementation of the above approach:
C++
#include<bits/stdc++.h>
using namespace std;
int power(int a, int b, int mod)
{
int aa = 1;
while(b)
{
if(b & 1)
{
aa = aa * a;
aa %= mod;
}
a = a * a;
a %= mod;
b /= 2;
}
return aa;
}
int product(int A[], int n)
{
int N = 100010;
int mod = 1000000007;
vector<int> prime(N, 1);
prime[0] = prime[1] = 0;
int i = 2;
while (i * i < N)
{
if (prime[i])
for (int j = 2 * i;
j <= N;j += i)
prime[j] = 0;
i += 1;
}
int t = power(2, n - 1, mod - 1);
int ans = 1;
for (int j = 0; j < n; j++)
{
int i = A[j];
if( prime[i])
{
ans *= power(i, t, mod);
ans %= mod;
}
}
return ans;
}
int main()
{
int A[] = {3, 7};
int n = sizeof(A) / sizeof(A[0]);
printf("%d", product(A, n));
}
|
Java
class GFG
{
static int power(int a, int b, int mod)
{
int aa = 1;
while(b > 0)
{
if(b % 2 == 1)
{
aa = aa * a;
aa %= mod;
}
a = a * a;
a %= mod;
b /= 2;
}
return aa;
}
static int product(int A[], int n)
{
int N = 100010;
int mod = 1000000007;
int []prime = new int[N];
for (int j = 0; j < N; j++)
{
prime[j] = 1;
}
prime[0] = prime[1] = 0;
int i = 2;
while (i * i < N)
{
if (prime[i] == 1)
for (int j = 2 * i;
j < N;j += i)
prime[j] = 0;
i += 1;
}
int t = power(2, n - 1, mod - 1);
int ans = 1;
for (int j = 0; j < n; j++)
{
i = A[j];
if( prime[i] == 1)
{
ans *= power(i, t, mod);
ans %= mod;
}
}
return ans;
}
public static void main (String[] args)
{
int A[] = {3, 7};
int n = A.length;
System.out.printf("%d", product(A, n));
}
}
|
Python3
def product(A):
N = 100010
mod = 1000000007
prime = [1] * N
prime[0] = prime[1] = 0
i = 2
while i * i < N:
if prime[i]:
for j in range(i * i, N, i):
prime[j] = 0
i += 1
n = len(A)
t = pow(2, n-1, mod-1)
ans = 1
for i in A:
if prime[i]:
ans *= pow(i, t, mod)
ans %= mod
return ans
A = [3, 7]
print(product(A))
|
C#
using System;
class GFG
{
static int power(int a, int b, int mod)
{
int aa = 1;
while(b > 0)
{
if(b % 2 == 1)
{
aa = aa * a;
aa %= mod;
}
a = a * a;
a %= mod;
b /= 2;
}
return aa;
}
static int product(int []A, int n)
{
int N = 100010;
int mod = 1000000007;
int []prime = new int[N];
for (int j = 0; j < N; j++)
{
prime[j] = 1;
}
prime[0] = prime[1] = 0;
int i = 2;
while (i * i < N)
{
if (prime[i] == 1)
for (int j = 2 * i;
j < N; j += i)
prime[j] = 0;
i += 1;
}
int t = power(2, n - 1, mod - 1);
int ans = 1;
for (int j = 0; j < n; j++)
{
i = A[j];
if( prime[i] == 1)
{
ans *= power(i, t, mod);
ans %= mod;
}
}
return ans;
}
public static void Main(String[] args)
{
int []A = {3, 7};
int n = A.Length;
Console.Write("{0}", product(A, n));
}
}
|
Javascript
<script>
function power(a, b, mod) {
let aa = 1;
while (b) {
if (b & 1) {
aa = aa * a;
aa %= mod;
}
a = a * a;
a %= mod;
b = Math.floor(b / 2);
}
return aa;
}
function product(A, n) {
let N = 100010;
let mod = 1000000007;
let prime = new Array(N).fill(1);
prime[0] = prime[1] = 0;
let i = 2;
while (i * i < N) {
if (prime[i])
for (let j = 2 * i;
j <= N; j += i)
prime[j] = 0;
i += 1;
}
let t = power(2, n - 1, mod - 1);
let ans = 1;
for (let j = 0; j < n; j++) {
let i = A[j];
if (prime[i]) {
ans *= power(i, t, mod);
ans %= mod;
}
}
return ans;
}
let A = [3, 7];
let n = A.length;
document.write(product(A, n));
</script>
|
Time Complexity: O(n), where n is the size of the given array.
Auxiliary Space: O(100010) ? O(1), no extra space is required, so it is a constant.
Share your thoughts in the comments
Please Login to comment...