Find maximum subset sum formed by partitioning any subset of array into 2 partitions with equal sum
Last Updated :
04 Oct, 2023
Given an array A containing N elements. Partition any subset of this array into two disjoint subsets such that both the subsets have an identical sum. Obtain the maximum sum that can be obtained after partitioning.
Note: It is not necessary to partition the entire array, that is any element might not contribute to any of the partition.
Examples:
Input: A = [1, 2, 3, 6]
Output: 6
Explanation: We have two disjoint subsets {1, 2, 3} and {6}, which have the same sum = 6
Input: A = [1, 2, 3, 4, 5, 6]
Output: 10
Explanation: We have two disjoint subsets {2, 3, 5} and {4, 6}, which have the same sum = 10.
Input: A = [1, 2]
Output: 0
Explanation: No subset can be partitioned into 2 disjoint subsets with identical sum
Naive Approach:
The above problem can be solved by brute force method using recursion. All the elements have three possibilities. Either it will contribute to partition 1 or partition 2 or will not be included in any of the partitions. We will perform these three operations on each of the elements and proceed to the next element in each recursive step.
Below is the implementation of the above approach:
C++
#include <bits/stdc++.h>
using namespace std;
int maxSum(int p0, int p1, int a[], int pos, int n)
{
if (pos == n) {
if (p0 == p1)
return p0;
else
return 0;
}
int ans = maxSum(p0, p1, a, pos + 1, n);
ans = max(ans, maxSum(p0 + a[pos], p1, a, pos + 1, n));
ans = max(ans, maxSum(p0, p1 + a[pos], a, pos + 1, n));
return ans;
}
int main()
{
int n = 4;
int a[n] = { 1, 2, 3, 6 };
cout << maxSum(0, 0, a, 0, n);
return 0;
}
|
Java
class GFG {
static int maxSum(int p0, int p1, int a[], int pos, int n)
{
if (pos == n) {
if (p0 == p1)
return p0;
else
return 0;
}
int ans = maxSum(p0, p1, a, pos + 1, n);
ans = Math.max(ans, maxSum(p0 + a[pos], p1, a, pos + 1, n));
ans = Math.max(ans, maxSum(p0, p1 + a[pos], a, pos + 1, n));
return ans;
}
public static void main (String[] args)
{
int n = 4;
int a[] = { 1, 2, 3, 6 };
System.out.println(maxSum(0, 0, a, 0, n));
}
}
|
Python3
def maxSum(p0, p1, a, pos, n) :
if (pos == n) :
if (p0 == p1) :
return p0;
else :
return 0;
ans = maxSum(p0, p1, a, pos + 1, n);
ans = max(ans, maxSum(p0 + a[pos], p1, a, pos + 1, n));
ans = max(ans, maxSum(p0, p1 + a[pos], a, pos + 1, n));
return ans;
if __name__ == "__main__" :
n = 4;
a = [ 1, 2, 3, 6 ];
print(maxSum(0, 0, a, 0, n));
|
C#
using System;
public class GFG {
static int maxSum(int p0, int p1, int []a, int pos, int n)
{
if (pos == n) {
if (p0 == p1)
return p0;
else
return 0;
}
int ans = maxSum(p0, p1, a, pos + 1, n);
ans = Math.Max(ans, maxSum(p0 + a[pos], p1, a, pos + 1, n));
ans = Math.Max(ans, maxSum(p0, p1 + a[pos], a, pos + 1, n));
return ans;
}
public static void Main (string[] args)
{
int n = 4;
int []a = { 1, 2, 3, 6 };
Console.WriteLine(maxSum(0, 0, a, 0, n));
}
}
|
Javascript
<script>
function maxSum(p0, p1, a, pos, n)
{
if (pos == n)
{
if (p0 == p1)
return p0;
else
return 0;
}
var ans = maxSum(p0, p1, a, pos + 1, n);
ans = Math.max(ans, maxSum(
p0 + a[pos], p1, a, pos + 1, n));
ans = Math.max(ans, maxSum(
p0, p1 + a[pos], a, pos + 1, n));
return ans;
}
var n = 4;
var a = [ 1, 2, 3, 6 ];
document.write(maxSum(0, 0, a, 0, n));
</script>
|
Time Complexity: 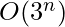
Auxiliary Space: O(n)
Memoization: Aa we can see there are multiple overlapping subproblems so instead of solving them again and again we can store each recursive call result in an array and use it .
C++
#include <bits/stdc++.h>
using namespace std;
int maxSum(int p0, int p1, int a[], int pos, int n,
vector<vector<int> >& dp)
{
if (pos == n) {
if (p0 == p1)
return p0;
else
return 0;
}
if (dp[pos][p0] != -1) {
return dp[pos][p0];
}
int ans = maxSum(p0, p1, a, pos + 1, n, dp);
ans = max(ans,
maxSum(p0 + a[pos], p1, a, pos + 1, n, dp));
ans = max(ans,
maxSum(p0, p1 + a[pos], a, pos + 1, n, dp));
return dp[pos][p0] = ans;
}
int maxSum(int p0, int p1, int a[], int pos, int n)
{
int sum = 0;
for (int i = 0; i < n; i++) {
sum += a[i];
}
vector<vector<int> > dp(n, vector<int>(sum + 1, -1));
return maxSum(p0, p1, a, pos, n, dp);
}
int main()
{
int n = 4;
int a[n] = { 1, 2, 3, 6 };
cout << maxSum(0, 0, a, 0, n);
return 0;
}
|
Java
import java.util.Arrays;
class GFG {
static int maxSum(int p0, int p1, int a[], int pos,
int n, int[][] dp)
{
if (pos == n) {
if (p0 == p1)
return p0;
else
return 0;
}
if (dp[pos][p0] != -1) {
return dp[pos][p0];
}
int ans = maxSum(p0, p1, a, pos + 1, n, dp);
ans = Math.max(
ans, maxSum(p0 + a[pos], p1, a, pos + 1, n,dp));
ans = Math.max(
ans, maxSum(p0, p1 + a[pos], a, pos + 1, n,dp));
return dp[pos][p0] = ans;
}
static int maxSum(int p0, int p1, int a[], int pos,
int n)
{
int sum = 0;
for (int i = 0; i < n; i++) {
sum += a[i];
}
int dp[][] = new int[n][sum + 1];
for (int row[] : dp) {
Arrays.fill(row, -1);
}
return maxSum(p0, p1, a, pos, n, dp);
}
public static void main(String[] args)
{
int n = 4;
int a[] = { 1, 2, 3, 6 };
System.out.println(maxSum(0, 0, a, 0, n));
}
}
|
Python3
def maxSum(p0, p1, a, pos, n, dp):
if pos == n:
if p0 == p1:
return p0
else:
return 0
if dp[pos][p0] != -1:
return dp[pos][p0]
ans = maxSum(p0, p1, a, pos + 1, n, dp)
ans = max(ans, maxSum(p0 + a[pos], p1, a, pos + 1, n, dp))
ans = max(ans, maxSum(p0, p1 + a[pos], a, pos + 1, n, dp))
dp[pos][p0] = ans
return dp[pos][p0]
def maxSumWrapper(a,n):
sum = 0
for i in range(n):
sum += a[i]
dp = [[-1 for i in range(sum+1)] for j in range(n)]
return maxSum(0, 0, a, 0, n, dp)
if __name__ == '__main__':
n = 4
a = [1, 2, 3, 6]
print(maxSumWrapper(a, n))
|
C#
using System;
class GFG
{
static int maxSum(int p0, int p1, int[] a, int pos,
int n, int[,] dp)
{
if (pos == n)
{
if (p0 == p1)
return p0;
else
return 0;
}
if (dp[pos, p0] != -1)
{
return dp[pos, p0];
}
int ans = maxSum(p0, p1, a, pos + 1, n, dp);
ans = Math.Max(
ans, maxSum(p0 + a[pos], p1, a, pos + 1, n, dp));
ans = Math.Max(
ans, maxSum(p0, p1 + a[pos], a, pos + 1, n, dp));
return dp[pos, p0] = ans;
}
static int maxSum(int p0, int p1, int[] a, int pos,
int n)
{
int sum = 0;
for (int i = 0; i < n; i++)
{
sum += a[i];
}
int[,] dp = new int[n, sum + 1];
for (int i = 0; i < n; i++)
{
for (int j = 0; j < sum + 1; j++)
{
dp[i, j] = -1;
}
}
return maxSum(p0, p1, a, pos, n, dp);
}
public static void Main(string[] args)
{
int n = 4;
int[] a = { 1, 2, 3, 6 };
Console.WriteLine(maxSum(0, 0, a, 0, n));
}
}
|
Javascript
function maxSum(p0, p1, a, pos, n,
dp) {
if (pos == n) {
if (p0 == p1)
return p0;
else
return 0;
}
if (dp[pos][p0] != -1) {
return dp[pos][p0];
}
let ans = maxSum(p0, p1, a, pos + 1, n, dp);
ans = Math.max(ans,
maxSum(p0 + a[pos], p1, a, pos + 1, n, dp));
ans = Math.max(ans,
maxSum(p0, p1 + a[pos], a, pos + 1, n, dp));
return dp[pos][p0] = ans;
}
function maxsum(p0, p1, a, pos, n) {
let sum = 0;
for (let i = 0; i < n; i++) {
sum += a[i];
}
let dp=new Array(n);
for(let i=0;i<n;i++)
{
dp[i]=new Array(sum+1);
for(let j=0;j<sum+1;j++)
dp[i][j]=-1;
}
return maxSum(p0, p1, a, pos, n, dp);
}
let n = 4;
let a = [1, 2, 3, 6];
console.log(maxsum(0, 0, a, 0, n));
|
Time Complexity: O(N*Sum), where Sum represents sum of all array elements.
Auxiliary Space: O(N*Sum) + O(N) .
Efficient Approach:
The above method can be optimized using Dynamic Programming method.
We will define our DP state as follows :
dp[i][j] = Max sum of group g0 considering the first i elements such that,
the difference between the sum of g0 and g1 is (sum of all elements – j), where j is the difference.
So, the answer would be dp[n][sum]
Now we might encounter, the difference between the sums is negative, lying in the range [-sum, +sum], where the sum is a summation of all elements. The minimum and maximum ranges occurring when one of the subsets is empty and the other one has all the elements. Due to this, in the DP state, we have defined j as (sum – diff). Thus, j will range from [0, 2*sum].
Below is the implementation of the above approach:
C++
#include <bits/stdc++.h>
using namespace std;
int maxSum(int a[], int n)
{
int sum = 0;
for (int i = 0; i < n; i++)
sum += a[i];
int limit = 2 * sum + 1;
int dp[n + 1][limit];
for (int i = 0; i < n + 1; i++) {
for (int j = 0; j < limit; j++)
dp[i][j] = INT_MIN;
}
dp[0][sum] = 0;
for (int i = 1; i <= n; i++) {
for (int j = 0; j < limit; j++) {
if ((j - a[i - 1]) >= 0 && dp[i - 1][j - a[i - 1]] != INT_MIN)
dp[i][j] = max(dp[i][j], dp[i - 1][j - a[i - 1]]
+ a[i - 1]);
if ((j + a[i - 1]) < limit && dp[i - 1][j + a[i - 1]] != INT_MIN)
dp[i][j] = max(dp[i][j], dp[i - 1][j + a[i - 1]]);
if (dp[i - 1][j] != INT_MIN)
dp[i][j] = max(dp[i][j], dp[i - 1][j]);
}
}
return dp[n][sum];
}
int main()
{
int n = 4;
int a[n] = { 1, 2, 3, 6 };
cout << maxSum(a, n);
return 0;
}
|
Java
class GFG {
final static int INT_MIN = Integer.MIN_VALUE;
static int maxSum(int a[], int n)
{
int sum = 0;
for (int i = 0; i < n; i++)
sum += a[i];
int limit = 2 * sum + 1;
int dp[][] = new int[n + 1][limit];
for (int i = 0; i < n + 1; i++) {
for (int j = 0; j < limit; j++)
dp[i][j] = INT_MIN;
}
dp[0][sum] = 0;
for (int i = 1; i <= n; i++) {
for (int j = 0; j < limit; j++) {
if ((j - a[i - 1]) >= 0 && dp[i - 1][j - a[i - 1]] != INT_MIN)
dp[i][j] = Math.max(dp[i][j], dp[i - 1][j - a[i - 1]]
+ a[i - 1]);
if ((j + a[i - 1]) < limit && dp[i - 1][j + a[i - 1]] != INT_MIN)
dp[i][j] = Math.max(dp[i][j], dp[i - 1][j + a[i - 1]]);
if (dp[i - 1][j] != INT_MIN)
dp[i][j] = Math.max(dp[i][j], dp[i - 1][j]);
}
}
return dp[n][sum];
}
public static void main (String[] args)
{
int n = 4;
int []a = { 1, 2, 3, 6 };
System.out.println(maxSum(a, n));
}
}
|
Python3
import numpy as np
import sys
INT_MIN = -(sys.maxsize - 1)
def maxSum(a, n) :
sum = 0;
for i in range(n) :
sum += a[i];
limit = 2 * sum + 1;
dp = np.zeros((n + 1,limit));
for i in range(n + 1) :
for j in range(limit) :
dp[i][j] = INT_MIN;
dp[0][sum] = 0;
for i in range(1, n + 1) :
for j in range(limit) :
if ((j - a[i - 1]) >= 0 and dp[i - 1][j - a[i - 1]] != INT_MIN) :
dp[i][j] = max(dp[i][j], dp[i - 1][j - a[i - 1]]
+ a[i - 1]);
if ((j + a[i - 1]) < limit and dp[i - 1][j + a[i - 1]] != INT_MIN) :
dp[i][j] = max(dp[i][j], dp[i - 1][j + a[i - 1]]);
if (dp[i - 1][j] != INT_MIN) :
dp[i][j] = max(dp[i][j], dp[i - 1][j]);
return dp[n][sum];
if __name__ == "__main__" :
n = 4;
a = [ 1, 2, 3, 6 ];
print(maxSum(a, n));
|
C#
using System;
class GFG {
static int INT_MIN = int.MinValue;
static int maxSum(int []a, int n)
{
int sum = 0;
for (int i = 0; i < n; i++)
sum += a[i];
int limit = 2 * sum + 1;
int [,]dp = new int[n + 1,limit];
for (int i = 0; i < n + 1; i++) {
for (int j = 0; j < limit; j++)
dp[i,j] = INT_MIN;
}
dp[0,sum] = 0;
for (int i = 1; i <= n; i++) {
for (int j = 0; j < limit; j++) {
if ((j - a[i - 1]) >= 0 && dp[i - 1,j - a[i - 1]] != INT_MIN)
dp[i,j] = Math.Max(dp[i,j], dp[i - 1,j - a[i - 1]]
+ a[i - 1]);
if ((j + a[i - 1]) < limit && dp[i - 1,j + a[i - 1]] != INT_MIN)
dp[i,j] = Math.Max(dp[i,j], dp[i - 1,j + a[i - 1]]);
if (dp[i - 1,j] != INT_MIN)
dp[i,j] = Math.Max(dp[i,j], dp[i - 1,j]);
}
}
return dp[n,sum];
}
public static void Main()
{
int n = 4;
int []a = { 1, 2, 3, 6 };
Console.WriteLine(maxSum(a, n));
}
}
|
Javascript
<script>
function maxSum(a, n)
{
var sum = 0;
for (var i = 0; i < n; i++)
sum += a[i];
var limit = 2 * sum + 1;
var dp = Array.from(Array(n+1), ()=>Array(limit));
for (var i = 0; i < n + 1; i++) {
for (var j = 0; j < limit; j++)
dp[i][j] = -1000000000;
}
dp[0][sum] = 0;
for (var i = 1; i <= n; i++) {
for (var j = 0; j < limit; j++) {
if ((j - a[i - 1]) >= 0 &&
dp[i - 1][j - a[i - 1]] != -1000000000)
dp[i][j] = Math.max(dp[i][j],
dp[i - 1][j - a[i - 1]] + a[i - 1]);
if ((j + a[i - 1]) < limit &&
dp[i - 1][j + a[i - 1]] != -1000000000)
dp[i][j] = Math.max(dp[i][j],
dp[i - 1][j + a[i - 1]]);
if (dp[i - 1][j] != -1000000000)
dp[i][j] = Math.max(dp[i][j], dp[i - 1][j]);
}
}
return dp[n][sum];
}
var n = 4;
var a = [1, 2, 3, 6];
document.write( maxSum(a, n));
</script>
|
Time Complexity: 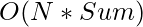 , where Sum represents sum of all array elements.
, where Sum represents sum of all array elements.
Auxiliary Space: 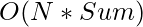
Efficient Approach : using array instead of 2d matrix to optimize space complexity
In previous code we can se that dp[i][j] is dependent upon dp[i-1] or dp[i] so we can assume that dp[i-1] is previous row and dp[i] is current row.
Implementations Steps :
- Create two vectors prev and curr each of size limit+1, where limit is a 2 * sum + 1.
- Initialize them with base cases.
- Now In previous code change dp[i] to curr and change dp[i-1] to prev to keep track only of the two main rows.
- After every iteration update previous row to current row to iterate further.
Implementation :
C++
#include <bits/stdc++.h>
using namespace std;
int maxSum(int a[], int n)
{
int sum = 0;
for (int i = 0; i < n; i++)
sum += a[i];
int limit = 2 * sum + 1;
vector<int>prev(limit +1 , INT_MIN);
vector<int>curr(limit +1 , INT_MIN);
prev[sum] = 0;
for (int i = 1; i <= n; i++) {
for (int j = 0; j < limit; j++) {
if ((j - a[i - 1]) >= 0 && prev[j - a[i - 1]] != INT_MIN)
curr[j] = max(curr[j], prev[j - a[i - 1]]
+ a[i - 1]);
if ((j + a[i - 1]) < limit && prev[j + a[i - 1]] != INT_MIN)
curr[j] = max(curr[j], prev[j + a[i - 1]]);
if (prev[j] != INT_MIN)
curr[j] = max(curr[j], prev[j]);
}
prev = curr;
}
return curr[sum];
}
int main()
{
int n = 4;
int a[n] = { 1, 2, 3, 6 };
cout << maxSum(a, n);
return 0;
}
|
Java
import java.util.*;
public class Main
{
public static int maxSum(int[] a, int n)
{
int sum = 0;
for (int i = 0; i < n; i++)
sum += a[i];
int limit = 2 * sum + 1;
int[] prev = new int[limit + 1];
int[] curr = new int[limit + 1];
Arrays.fill(prev, Integer.MIN_VALUE);
Arrays.fill(curr, Integer.MIN_VALUE);
prev[sum] = 0;
for (int i = 1; i <= n; i++) {
for (int j = 0; j < limit; j++) {
if ((j - a[i - 1]) >= 0
&& prev[j - a[i - 1]]
!= Integer.MIN_VALUE)
curr[j] = Math.max(curr[j],
prev[j - a[i - 1]]
+ a[i - 1]);
if ((j + a[i - 1]) < limit
&& prev[j + a[i - 1]]
!= Integer.MIN_VALUE)
curr[j] = Math.max(curr[j],
prev[j + a[i - 1]]);
if (prev[j] != Integer.MIN_VALUE)
curr[j] = Math.max(curr[j], prev[j]);
}
prev = curr.clone();
}
return curr[sum];
}
public static void main(String[] args)
{
int n = 4;
int[] a = { 1, 2, 3, 6 };
System.out.println(maxSum(a, n));
}
}
|
Python
def max_sum(a, n):
total_sum = sum(a)
limit = 2 * total_sum + 1
prev = [float('-inf')] * (limit + 1)
curr = [float('-inf')] * (limit + 1)
prev[total_sum] = 0
for i in range(1, n + 1):
for j in range(limit):
if (j - a[i - 1]) >= 0 and prev[j - a[i - 1]] != float('-inf'):
curr[j] = max(curr[j], prev[j - a[i - 1]] + a[i - 1])
if (j + a[i - 1]) < limit and prev[j + a[i - 1]] != float('-inf'):
curr[j] = max(curr[j], prev[j + a[i - 1]])
if prev[j] != float('-inf'):
curr[j] = max(curr[j], prev[j])
prev = curr[:]
return curr[total_sum]
if __name__ == "__main__":
n = 4
a = [1, 2, 3, 6]
print(max_sum(a, n))
|
C#
using System;
using System.Collections.Generic;
class GFG
{
static int MaxSum(int[] a, int n)
{
int sum = 0;
for (int i = 0; i < n; i++)
sum += a[i];
int limit = 2 * sum + 1;
List<int> prev = new List<int>();
List<int> curr = new List<int>();
for (int i = 0; i <= limit; i++)
{
prev.Add(int.MinValue);
curr.Add(int.MinValue);
}
prev[sum] = 0;
for (int i = 1; i <= n; i++)
{
for (int j = 0; j < limit; j++)
{
if ((j - a[i - 1]) >= 0 && prev[j - a[i - 1]] != int.MinValue)
curr[j] = Math.Max(curr[j], prev[j - a[i - 1]] + a[i - 1]);
if ((j + a[i - 1]) < limit && prev[j + a[i - 1]] != int.MinValue)
curr[j] = Math.Max(curr[j], prev[j + a[i - 1]]);
if (prev[j] != int.MinValue)
curr[j] = Math.Max(curr[j], prev[j]);
}
prev = new List<int>(curr);
}
return curr[sum];
}
static void Main(string[] args)
{
int n = 4;
int[] a = { 1, 2, 3, 6 };
Console.WriteLine(MaxSum(a, n));
}
}
|
Javascript
function maxSum(a, n) {
let sum = 0;
for (let i = 0; i < n; i++)
sum += a[i];
let limit = 2 * sum + 1;
let prev = new Array(limit + 1).fill(Number.MIN_SAFE_INTEGER);
let curr = new Array(limit + 1).fill(Number.MIN_SAFE_INTEGER);
prev[sum] = 0;
for (let i = 1; i <= n; i++) {
for (let j = 0; j < limit; j++) {
if ((j - a[i - 1]) >= 0 && prev[j - a[i - 1]] != Number.MIN_SAFE_INTEGER)
curr[j] = Math.max(curr[j], prev[j - a[i - 1]] + a[i - 1]);
if ((j + a[i - 1]) < limit && prev[j + a[i - 1]] != Number.MIN_SAFE_INTEGER)
curr[j] = Math.max(curr[j], prev[j + a[i - 1]]);
if (prev[j] != Number.MIN_SAFE_INTEGER)
curr[j] = Math.max(curr[j], prev[j]);
}
prev = [...curr];
}
return curr[sum];
}
let n = 4;
let a = [1, 2, 3, 6];
console.log(maxSum(a, n));
|
Output:
6
Time Complexity: O(N*Sum)
Auxiliary Space: O(Sum)
Like Article
Suggest improvement
Share your thoughts in the comments
Please Login to comment...