Preparata Algorithm
Last Updated :
22 Mar, 2023
Preparata’s algorithm is a recursive Divide and Conquer Algorithm where the rank of each input key is computed and the keys are outputted according to their ranks.
C++
m[i, j] := M[i, j]
for 1 <= i, j <= n in parallel;
for
r : = 1 to logn do
{
Step 1. In parallel set q[i, j, k] := m[i, j] + m[j, k] for
1 <= i, j, k <= n.
Step 2. In parallel set m[i, j] := min
{
q[i, l, j], q[i, 2, j], ..., q[i, n, j]
}
for
1 <= i, j <= n.
}
Put M(i)(i):=0 for all i and M(i)(j):=m[i, j] for i≠j
|
In the above procedure O(N3) global memory is used by using the variables m[i, j] for 1 ≤ i, j ≤ N and q[i, j, k] for 1 ≤ i, j, k ≤ N.
- Initializing m[ ] that takes O(N2) time.
- Step 1 of the above algorithm takes O(1) time while using 3 processors.
- In Step 2, N2 number of different m[i, j]’s are computed.
The computation of a single m[z, j] involves computing a minimum of N numbers and hence can be completed in O(1) time using N2 CRCW PRAM processors. In fact, this minimum can also be computed in O(1) time using n(1 + e) processors for any fixed e > 0.
Step 2 can be completed in O(1) time using n(3 + e) common CRCW PRAM processors. Thus, the for loop runs in O(log N) time. The final computation of M also can be done in O(1) time using N2 processors.
The correctness of the above algorithm can be proven by induction on R. It can be shown that the value of m[i, j] at the end of the rth iteration of the for loop is min, and the minimum is taken over all the sequences of elements of {1, 2, …, N} such that k < 2R. The above algorithm can be specialized to solve several problems including the transitive closure, connected components, minimum spanning tree, and so on.
Let k1, k2, …, kn be the input sequence. Preparata’s algorithm partitions the input into log N parts K1, K2, …, if log N; where there are N/log N keys in each part.
If k is any key in the input, its rank in the input is computed as follows. First, the rank Ri of k is computed for each i, 1< i < log N. Then, the total rank of k is computed as 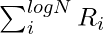 . One of the results that make the use of the above algorithm.
. One of the results that make the use of the above algorithm.
The details of Preparata’s algorithm are given below.
Consider T(N) to be the run time of Preparata’s algorithm using N*log N processors. Clearly, step 1 takes T(N/log N) time and steps 2 and 3 together take O(log(log N)) time. Thus, there is
T(n) = T(N/log N) + O(log(log N))
which can be solved by repeated substitution to get T(N) = O(log N). Also, the number of processors used in each step is N*log N.
Preparata’s Sorting Algorithm
Below are the steps for the Preparata’s Sorting Algorithm:
- If N is a small constant, sort the keys using any algorithm and quit.
- Partition the given N keys into log N parts, with N/(log N) keys in each part.
- Sort each part recursively and separately in parallel, assigning N processors to each part. Let S1, S2, …, Slog N be the sorted sequences.
- Merge Si with Sj for 1< i, j < log N in parallel. This can be done by allocating N/(log N) processors to each pair(i, j). That is, using N*log N processors, this step can be accomplished in O(log(log N)) time with the algorithm. As a by-product of this merging step, the rank is computed of each key in each one of the Si‘s(1 < i < log N).
- Allocate log N processors to compute the rank of each key in the original input. This is done in parallel for all the keys by adding the log N ranks computed (for each key) in step 2. This can be done in O(log(log N)) time using the prefix computation algorithm.
- Finally, the keys are written in the order of their ranks.
Below is the implementation of the above approach:
C++
#include <iostream>
#include <vector>
using namespace std;
class Point {
public:
int x, y;
Point(int x, int y) {
this->x = x;
this->y = y;
}
};
class LeftIndex {
public:
int leftMostIndex(Point points[], int n) {
int min = 0;
for (int i = 1; i < n; i++) {
if (points[i].x < points[min].x)
min = i;
else if (points[i].x == points[min].x) {
if (points[i].y > points[min].y)
min = i;
}
}
return min;
}
int parallel(Point p, Point q, Point r) {
int val = (q.y - p.y) * (r.x - q.x) - (q.x - p.x) * (r.y - q.y);
if (val == 0)
return 0;
else if (val > 0)
return 1;
else
return 2;
}
void preparata(Point points[], int n) {
if (n < 3)
return;
int l = leftMostIndex(points, n);
vector<Point> pre;
int p = l, q;
do {
pre.push_back(points[p]);
q = (p + 1) % n;
for (int i = 0; i < n; i++) {
if (parallel(points[p], points[i], points[q]) == 2)
q = i;
}
p = q;
} while (p != l);
for (int i = 0; i < pre.size(); i++)
cout << "(" << pre[i].x << ", " << pre[i].y << ")" << endl;
}
};
int main() {
Point points[] = {Point(0, 3), Point(2, 2), Point(1, 1), Point(2, 1), Point(3, 0), Point(0, 0), Point(3, 3)};
int n = sizeof(points) / sizeof(points[0]);
LeftIndex obj;
obj.preparata(points, n);
return 0;
}
|
Java
import java.util.*;
class Point
{
int x, y;
Point(int x, int y)
{
this.x = x;
this.y = y;
}
}
class LeftIndex
{
int leftMostIndex(Point points[], int n)
{
int min = 0;
for (int i = 1; i < n; i++)
{
if (points[i].x < points[min].x)
min = i;
else if (points[i].x == points[min].x)
{
if (points[i].y > points[min].y)
min = i;
}
}
return min;
}
int parallel(Point p, Point q, Point r)
{
int val = (q.y - p.y) * (r.x - q.x) -
(q.x - p.x) * (r.y - q.y);
if (val == 0)
return 0;
else if (val > 0)
return 1;
else
return 2;
}
void preparata(Point points[], int n)
{
if (n < 3)
return;
int l = leftMostIndex(points, n);
List<Point> pre = new ArrayList<Point>();
int p = l, q;
do
{
pre.add(points[p]);
q = (p + 1) % n;
for (int i = 0; i < n; i++)
{
if (parallel(points[p], points[i],
points[q]) == 2)
q = i;
}
p = q;
} while (p != l);
for (int i = 0; i < pre.size(); i++)
System.out.println("("+ pre.get(i).x +
", "+ pre.get(i).y +")");
}
public static void main(String[] args)
{
Point points[] = new Point[7];
points[0] = new Point(0, 3);
points[1] = new Point(2, 2);
points[2] = new Point(1, 1);
points[3] = new Point(2, 1);
points[4] = new Point(3, 0);
points[5] = new Point(0, 0);
points[6] = new Point(3, 3);
LeftIndex obj = new LeftIndex();
obj.preparata(points, 7);
} }
|
Python3
class func:
def __init__(self, x, y):
self.x = x
self.y = y
def Left_index(points):
minn = 0
for i in range(1, len(points)):
if points[i].x < points[minn].x:
minn = i
elif points[i].x == points[minn].x:
if points[i].y > points[minn].y:
minn = i
return minn
def parallel(p, q, r):
val = (q.y - p.y) * (r.x - q.x) - \
(q.x - p.x) * (r.y - q.y)
if val == 0:
return 0
elif val > 0:
return 1
else:
return 2
def preparata(points, n):
if n < 3:
return
l = Left_index(points)
pre = []
p = l
q = 0
while(True):
pre.append(p)
q = (p + 1) % n
for i in range(n):
if(parallel(points[p],
points[i], points[q]) == 2):
q = i
p = q
if(p == l):
break
for each in pre:
print(points[each].x, points[each].y)
algo = []
algo.append(func(0, 3))
algo.append(func(2, 2))
algo.append(func(1, 1))
algo.append(func(2, 1))
algo.append(func(3, 0))
algo.append(func(0, 0))
algo.append(func(3, 3))
preparata(algo, len(algo))
|
C#
using System;
using System.Collections.Generic;
public class Point
{
public int x, y;
public Point(int x, int y)
{
this.x = x;
this.y = y;
}
}
public class LeftIndex
{
public int leftMostIndex(Point[] points, int n)
{
int min = 0;
for (int i = 1; i < n; i++)
{
if (points[i].x < points[min].x)
min = i;
else if (points[i].x == points[min].x)
{
if (points[i].y > points[min].y)
min = i;
}
}
return min;
}
public int parallel(Point p, Point q, Point r)
{
int val = (q.y - p.y) * (r.x - q.x) - (q.x - p.x) * (r.y - q.y);
if (val == 0)
return 0;
else if (val > 0)
return 1;
else
return 2;
}
public void preparata(Point[] points, int n)
{
if (n < 3)
return;
int l = leftMostIndex(points, n);
List<Point> pre = new List<Point>();
int p = l, q;
do
{
pre.Add(points[p]);
q = (p + 1) % n;
for (int i = 0; i < n; i++)
{
if (parallel(points[p], points[i], points[q]) == 2)
q = i;
}
p = q;
} while (p != l);
for (int i = 0; i < pre.Count; i++)
Console.WriteLine("(" + pre[i].x + ", " + pre[i].y + ")");
}
}
class Program
{
static void Main(string[] args)
{
Point[] points = { new Point(0, 3), new Point(2, 2), new Point(1, 1), new Point(2, 1), new Point(3, 0), new Point(0, 0), new Point(3, 3) };
int n = points.Length;
LeftIndex obj = new LeftIndex();
obj.preparata(points, n);
Console.ReadLine();
}
}
|
Javascript
function Left_index(points) {
let minn = 0;
for (let i = 1; i < points.length; i++) {
if (points[i].x < points[minn].x) {
minn = i;
}
else if (points[i].x == points[minn].x) {
if (points[i].y > points[minn].y) {
minn = i;
}
}
}
return minn;
}
function parallel(p, q, r) {
let val = (q.y - p.y) * (r.x - q.x) -
(q.x - p.x) * (r.y - q.y);
if (val == 0) {
return 0;
}
else if (val > 0) {
return 1;
}
else {
return 2;
}
}
function preparata(points, n) {
if (n < 3) {
return;
}
let l = Left_index(points);
let pre = [];
let p = l;
let q = 0;
while(true) {
pre.push(p);
q = (p + 1) % n;
for (let i = 0; i < n; i++) {
if (parallel(points[p],
points[i], points[q]) == 2) {
q = i;
}
}
p = q;
if (p == l) {
break;
}
}
for (let each of pre) {
console.log(points[each].x, points[each].y);
}
}
let algo = [];
algo.push({x: 0, y: 3});
algo.push({x: 2, y: 2});
algo.push({x: 1, y: 1});
algo.push({x: 2, y: 1});
algo.push({x: 3, y: 0});
algo.push({x: 0, y: 0});
algo.push({x: 3, y: 3});
preparata(algo, algo.length);
|
Share your thoughts in the comments
Please Login to comment...