DFS traversal of a tree using recursion

Given a Binary tree, Traverse it using DFS using recursion.

Unlike linear data structures (Array, Linked List, Queues, Stacks, etc) which have only one logical way to traverse them, trees can be traversed in different ways. Generally there are 2 widely used ways for traversing trees:

• DFS or Depth First Search
• BFS or Breadth First Search

In this article, traversal using DFS has been discussed. Please see this post for Breadth First Traversal.

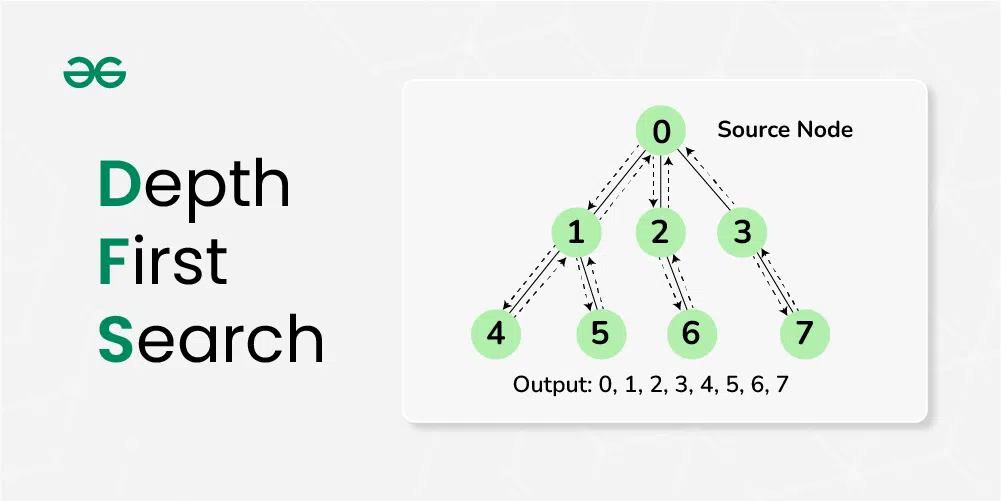
Depth-first search

DFS (Depth-first search) is technique used for traversing tree or graph. Here backtracking is used for traversal. In this traversal first the deepest node is visited and then backtracks to it’s parent node if no sibling of that node exist.

DFS Traversal of a Graph vs Tree

In graph, there might be cycles and dis-connectivity. Unlike graph, tree does not contain cycle and always connected. So DFS of a tree is relatively easier. We can simply begin from a node, then traverse its adjacent (or children) without caring about cycles. And if we begin from a single node (root), and traverse this way, it is guaranteed that we traverse the whole tree as there is no dis-connectivity,

Examples:

Tree:
Example Tree

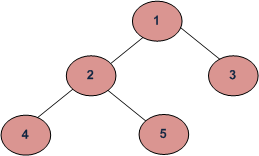
Therefore, the Depth First Traversals of this Tree will be:
(a) Inorder   (Left, Root, Right) : 4 2 5 1 3
(b) Preorder  (Root, Left, Right) : 1 2 4 5 3
(c) Postorder (Left, Right, Root) : 4 5 2 3 1

Below are the Tree traversals through DFS using recursion:

1. Inorder Traversal (Practice):

   Example: Inorder traversal for the above-given figure is 4 2 5 1 3.

   Algorithm Inorder(tree)
      1. Traverse the left subtree, i.e., call Inorder(left-subtree)
      2. Visit the root.
      3. Traverse the right subtree, i.e., call Inorder(right-subtree)
   

   Implementation:

   C++

   
   

   
   
   

   // C program for different tree traversals #include <iostream> using namespace std;    /* A binary tree node has data, pointer to left child and a pointer to right child */ struct Node {     int data;     struct Node *left, *right;     Node(int data)     {         this->data = data;         left = right = NULL;     } };    /* Given a binary tree, print its nodes in inorder*/ void printInorder(struct Node* node) {     if (node == NULL)         return;        /* first recur on left child */     printInorder(node->left);        /* then print the data of node */     cout << node->data << " ";        /* now recur on right child */     printInorder(node->right); }    /* Driver program to test above functions*/ int main() {     struct Node* root = new Node(1);     root->left = new Node(2);     root->right = new Node(3);     root->left->left = new Node(4);     root->left->right = new Node(5);        cout << "\nInorder traversal of binary tree is \n";     printInorder(root);        return 0; }

   C

   
   

   
   
   

   // C program for different tree traversals #include <stdio.h> #include <stdlib.h>    /* A binary tree node has data, pointer to left child    and a pointer to right child */ struct node {     int data;     struct node* left;     struct node* right; };    /* Helper function that allocates a new node with the    given data and NULL left and right pointers. */ struct node* newNode(int data) {     struct node* node = (struct node*)         malloc(sizeof(struct node));     node->data = data;     node->left = NULL;     node->right = NULL;        return (node); }    /* Given a binary tree, print its nodes in inorder*/ void printInorder(struct node* node) {     if (node == NULL)         return;        /* first recur on left child */     printInorder(node->left);        /* then print the data of node */     printf("%d ", node->data);        /* now recur on right child */     printInorder(node->right); }    /* Driver program to test above functions*/ int main() {     struct node* root = newNode(1);     root->left = newNode(2);     root->right = newNode(3);     root->left->left = newNode(4);     root->left->right = newNode(5);        printf("\nInorder traversal of binary tree is \n");     printInorder(root);        getchar();     return 0; }

   Java

   
   

   
   
   

   // Java program for different tree traversals    /* Class containing left and right child of current    node and key value*/ class Node {     int key;     Node left, right;        public Node(int item)     {         key = item;         left = right = null;     } }    class BinaryTree {     // Root of Binary Tree     Node root;        BinaryTree()     {         root = null;     }        /* Given a binary tree, print its nodes in inorder*/     void printInorder(Node node)     {         if (node == null)             return;            /* first recur on left child */         printInorder(node.left);            /* then print the data of node */         System.out.print(node.key + " ");            /* now recur on right child */         printInorder(node.right);     }        // Wrappers over above recursive functions     void printInorder() { printInorder(root); }        // Driver method     public static void main(String[] args)     {         BinaryTree tree = new BinaryTree();         tree.root = new Node(1);         tree.root.left = new Node(2);         tree.root.right = new Node(3);         tree.root.left.left = new Node(4);         tree.root.left.right = new Node(5);            System.out.println("\nInorder traversal of binary tree is ");         tree.printInorder();     } }

   Python

   
   

   
   
   

   # Python program to for tree traversals    # A class that represents an individual node in a # Binary Tree class Node:     def __init__(self, key):         self.left = None         self.right = None         self.val = key       # A function to do inorder tree traversal def printInorder(root):        if root:            # First recur on left child         printInorder(root.left)            # then print the data of node         print(root.val),            # now recur on right child         printInorder(root.right)               # Driver code root = Node(1) root.left = Node(2) root.right = Node(3) root.left.left = Node(4) root.left.right = Node(5)    print "\nInorder traversal of binary tree is" printInorder(root)

   C#

   
   

   
   
   

   // C# program for different tree traversals using System;        /* Class containing left and right child of current node and key value*/ class Node  {     public int key;     public Node left, right;        public Node(int item)     {         key = item;         left = right = null;     } }    public class BinaryTree  {     // Root of Binary Tree     Node root;        BinaryTree()     {         root = null;     }        /* Given a binary tree, print its nodes in inorder*/     void printInorder(Node node)     {         if (node == null)             return;            /* first recur on left child */         printInorder(node.left);            /* then print the data of node */         Console.Write(node.key + " ");            /* now recur on right child */         printInorder(node.right);     }        // Wrappers over above recursive functions     void printInorder()      {          printInorder(root);      }        // Driver code     public static void Main(String[] args)     {         BinaryTree tree = new BinaryTree();         tree.root = new Node(1);         tree.root.left = new Node(2);         tree.root.right = new Node(3);         tree.root.left.left = new Node(4);         tree.root.left.right = new Node(5);            Console.WriteLine("\nInorder traversal of binary tree is ");         tree.printInorder();     } }    // This code is contributed by PrinciRaj1992

   Output:

   Inorder traversal of binary tree is 
   4 2 5 1 3
   

   Uses of Inorder:
   In case of binary search trees (BST), Inorder traversal gives nodes in non-decreasing order. To get nodes of BST in non-increasing order, a variation of Inorder traversal where Inorder traversal s reversed can be used.

2. Preorder Traversal (Practice):

   Example: Preorder traversal for the above given figure is 1 2 4 5 3.

   
   
   
   

   Algorithm Preorder(tree)
      1. Visit the root.
      2. Traverse the left subtree, i.e., call Preorder(left-subtree)
      3. Traverse the right subtree, i.e., call Preorder(right-subtree)
   

   Implementation:

   C++

   
   

   
   
   

   // C program for different tree traversals #include <iostream> using namespace std;    /* A binary tree node has data, pointer to left child and a pointer to right child */ struct Node {     int data;     struct Node *left, *right;     Node(int data)     {         this->data = data;         left = right = NULL;     } };    /* Given a binary tree, print its nodes in preorder*/ void printPreorder(struct Node* node) {     if (node == NULL)         return;        /* first print data of node */     cout << node->data << " ";        /* then recur on left sutree */     printPreorder(node->left);        /* now recur on right subtree */     printPreorder(node->right); }    /* Driver program to test above functions*/ int main() {     struct Node* root = new Node(1);     root->left = new Node(2);     root->right = new Node(3);     root->left->left = new Node(4);     root->left->right = new Node(5);        cout << "\nPreorder traversal of binary tree is \n";     printPreorder(root);        return 0; }

   C

   
   

   
   
   

   // C program for different tree traversals #include <stdio.h> #include <stdlib.h>    /* A binary tree node has data, pointer to left child    and a pointer to right child */ struct node {     int data;     struct node* left;     struct node* right; };    /* Helper function that allocates a new node with the    given data and NULL left and right pointers. */ struct node* newNode(int data) {     struct node* node = (struct node*)         malloc(sizeof(struct node));     node->data = data;     node->left = NULL;     node->right = NULL;        return (node); }    /* Given a binary tree, print its nodes in preorder*/ void printPreorder(struct node* node) {     if (node == NULL)         return;        /* first print data of node */     printf("%d ", node->data);        /* then recur on left sutree */     printPreorder(node->left);        /* now recur on right subtree */     printPreorder(node->right); }    /* Driver program to test above functions*/ int main() {     struct node* root = newNode(1);     root->left = newNode(2);     root->right = newNode(3);     root->left->left = newNode(4);     root->left->right = newNode(5);        printf("\nPreorder traversal of binary tree is \n");     printPreorder(root);        getchar();     return 0; }

   Java

   
   

   
   
   

   // Java program for different tree traversals    /* Class containing left and right child of current    node and key value*/ class Node {     int key;     Node left, right;        public Node(int item)     {         key = item;         left = right = null;     } }    class BinaryTree {     // Root of Binary Tree     Node root;        BinaryTree()     {         root = null;     }        /* Given a binary tree, print its nodes in preorder*/     void printPreorder(Node node)     {         if (node == null)             return;            /* first print data of node */         System.out.print(node.key + " ");            /* then recur on left sutree */         printPreorder(node.left);            /* now recur on right subtree */         printPreorder(node.right);     }        // Wrappers over above recursive functions     void printPreorder() { printPreorder(root); }        // Driver method     public static void main(String[] args)     {         BinaryTree tree = new BinaryTree();         tree.root = new Node(1);         tree.root.left = new Node(2);         tree.root.right = new Node(3);         tree.root.left.left = new Node(4);         tree.root.left.right = new Node(5);            System.out.println("Preorder traversal of binary tree is ");         tree.printPreorder();     } }

   Python

   
   

   
   
   

   # Python program to for tree traversals    # A class that represents an individual node in a # Binary Tree class Node:     def __init__(self, key):         self.left = None         self.right = None         self.val = key    # A function to do preorder tree traversal def printPreorder(root):        if root:            # First print the data of node         print(root.val),            # Then recur on left child         printPreorder(root.left)            # Finally recur on right child         printPreorder(root.right)       # Driver code root = Node(1) root.left = Node(2) root.right = Node(3) root.left.left = Node(4) root.left.right = Node(5) print "Preorder traversal of binary tree is" printPreorder(root)

   C#

   
   

   
   
   

   // C# program for different tree traversals using System;    /* Class containing left and right child of current node and key value*/ public class Node  {     public int key;     public Node left, right;        public Node(int item)     {         key = item;         left = right = null;     } }    public class BinaryTree  {     // Root of Binary Tree     Node root;        BinaryTree()     {         root = null;     }        /* Given a binary tree, print its nodes in preorder*/     void printPreorder(Node node)     {         if (node == null)             return;            /* first print data of node */         Console.Write(node.key + " ");            /* then recur on left sutree */         printPreorder(node.left);            /* now recur on right subtree */         printPreorder(node.right);     }        // Wrappers over above recursive functions     void printPreorder() { printPreorder(root); }        // Driver method     public static void Main()     {         BinaryTree tree = new BinaryTree();         tree.root = new Node(1);         tree.root.left = new Node(2);         tree.root.right = new Node(3);         tree.root.left.left = new Node(4);         tree.root.left.right = new Node(5);            Console.WriteLine("Preorder traversal of binary tree is ");         tree.printPreorder();     } }    /* This code contributed by PrinciRaj1992 */

   Output:

   Preorder traversal of binary tree is 
   1 2 4 5 3
   

   Uses of Preorder:
   Preorder traversal is used to create a copy of the tree. Preorder traversal is also used to get prefix expression on of an expression tree. Please see http://en.wikipedia.org/wiki/Polish_notation to know why prefix expressions are useful.

3. Postorder Traversal (Practice):

   Example: Postorder traversal for the above given Tree is 4 5 2 3 1.

   Algorithm Postorder(tree)
      1. Traverse the left subtree, i.e., call Postorder(left-subtree)
      2. Traverse the right subtree, i.e., call Postorder(right-subtree)
      3. Visit the root.
   

   Implementation:

   C++

   
   

   
   
   

   // C program for different tree traversals #include <iostream> using namespace std;    /* A binary tree node has data, pointer to left child and a pointer to right child */ struct Node {     int data;     struct Node *left, *right;     Node(int data)     {         this->data = data;         left = right = NULL;     } };    /* Given a binary tree, print its nodes according to the "bottom-up" postorder traversal. */ void printPostorder(struct Node* node) {     if (node == NULL)         return;        // first recur on left subtree     printPostorder(node->left);        // then recur on right subtree     printPostorder(node->right);        // now deal with the node     cout << node->data << " "; }    /* Driver program to test above functions*/ int main() {     struct Node* root = new Node(1);     root->left = new Node(2);     root->right = new Node(3);     root->left->left = new Node(4);     root->left->right = new Node(5);        cout << "\nPostorder traversal of binary tree is \n";     printPostorder(root);        return 0; }

   C

   
   

   
   
   

   // C program for different tree traversals #include <stdio.h> #include <stdlib.h>    /* A binary tree node has data, pointer to left child    and a pointer to right child */ struct node {     int data;     struct node* left;     struct node* right; };    /* Helper function that allocates a new node with the    given data and NULL left and right pointers. */ struct node* newNode(int data) {     struct node* node = (struct node*)         malloc(sizeof(struct node));     node->data = data;     node->left = NULL;     node->right = NULL;        return (node); }    /* Given a binary tree, print its nodes according to the   "bottom-up" postorder traversal. */ void printPostorder(struct node* node) {     if (node == NULL)         return;        // first recur on left subtree     printPostorder(node->left);        // then recur on right subtree     printPostorder(node->right);        // now deal with the node     printf("%d ", node->data); }    /* Driver program to test above functions*/ int main() {     struct node* root = newNode(1);     root->left = newNode(2);     root->right = newNode(3);     root->left->left = newNode(4);     root->left->right = newNode(5);        printf("\nPostorder traversal of binary tree is \n");     printPostorder(root);        getchar();     return 0; }

   Java

   
   

   
   
   

   // Java program for different tree traversals    /* Class containing left and right child of current    node and key value*/ class Node {     int key;     Node left, right;        public Node(int item)     {         key = item;         left = right = null;     } }    class BinaryTree {     // Root of Binary Tree     Node root;        BinaryTree()     {         root = null;     }        /* Given a binary tree, print its nodes according to the       "bottom-up" postorder traversal. */     void printPostorder(Node node)     {         if (node == null)             return;            // first recur on left subtree         printPostorder(node.left);            // then recur on right subtree         printPostorder(node.right);            // now deal with the node         System.out.print(node.key + " ");     }        // Wrappers over above recursive functions     void printPostorder() { printPostorder(root); }        // Driver method     public static void main(String[] args)     {         BinaryTree tree = new BinaryTree();         tree.root = new Node(1);         tree.root.left = new Node(2);         tree.root.right = new Node(3);         tree.root.left.left = new Node(4);         tree.root.left.right = new Node(5);            System.out.println("\nPostorder traversal of binary tree is ");         tree.printPostorder();     } }

   Python

   
   

   
   
   

   # Python program to for tree traversals    # A class that represents an individual node in a # Binary Tree class Node:     def __init__(self, key):         self.left = None         self.right = None         self.val = key               # A function to do postorder tree traversal def printPostorder(root):        if root:            # First recur on left child         printPostorder(root.left)            # the recur on right child         printPostorder(root.right)            # now print the data of node         print(root.val),       # Driver code root = Node(1) root.left = Node(2) root.right = Node(3) root.left.left = Node(4) root.left.right = Node(5)    print "\nPostorder traversal of binary tree is" printPostorder(root)

   C#

   
   

   
   
   

   // C# program for different tree traversals using System;    /* Class containing left and right child of current node and key value*/ public class Node  {     public int key;     public Node left, right;        public Node(int item)     {         key = item;         left = right = null;     } }    public class BinaryTree  {     // Root of Binary Tree     Node root;        BinaryTree()     {         root = null;     }        /* Given a binary tree, print its nodes according to the     "bottom-up" postorder traversal. */     void printPostorder(Node node)     {         if (node == null)             return;            // first recur on left subtree         printPostorder(node.left);            // then recur on right subtree         printPostorder(node.right);            // now deal with the node         Console.Write(node.key + " ");     }        // Wrappers over above recursive functions     void printPostorder() { printPostorder(root); }        // Driver code     public static void Main(String[] args)     {         BinaryTree tree = new BinaryTree();         tree.root = new Node(1);         tree.root.left = new Node(2);         tree.root.right = new Node(3);         tree.root.left.left = new Node(4);         tree.root.left.right = new Node(5);            Console.WriteLine("\nPostorder traversal of binary tree is ");         tree.printPostorder();     } }    // This code contributed by Rajput-Ji

   Output:

   Postorder traversal of binary tree is 
   4 5 2 3 1
   

   Uses of Postorder:
   Postorder traversal is used to delete the tree. Please see the question for deletion of tree for details. Postorder traversal is also useful to get the postfix expression of an expression tree. Please see http://en.wikipedia.org/wiki/Reverse_Polish_notation to for the usage of postfix expression.

Implementing all traversals using DFS

Preorder traversal of binary tree is
1 2 4 5 3 
Inorder traversal of binary tree is
4 2 5 1 3 
Postorder traversal of binary tree is
4 5 2 3 1

Time Complexity: O(n)
Auxiliary Space : If we don’t consider size of stack for function calls then O(1) otherwise O(n).

Attention reader! Don’t stop learning now. Get hold of all the important DSA concepts with the DSA Self Paced Course at a student-friendly price and become industry ready.  To complete your preparation from learning a language to DS Algo and many more,  please refer Complete Interview Preparation Course.

In case you wish to attend live classes with experts, please refer DSA Live Classes for Working Professionals and Competitive Programming Live for Students.