Polynomials Class 10 Maths Notes Chapter 2

CBSE Class 10 Maths Notes Chapter 4 Polynomials are provided to support student’s education. We believe that students’ learning and development are of utmost importance, and that’s why we have created these comprehensive notes to help them comprehend the complex subject of Polynomials better.

The NCERT Class 10 Maths textbook’s Chapter 4 explores the realm of Polynomials and covers various concepts such as finding the polynomial degree, types of polynomials, zeros of polynomials, and more. Our notes aim to provide students with a complete summary of the entire chapter, including all essential topics, formulae, and concepts necessary to succeed in their exams.

What is Polynomials?

An algebraic expression in the form of a₀+a₁x¹+a₂x²+….+a_nxⁿ where a₀, a₁, a₂, …, a_n represents the real numbers, n represents the positive integers and x represents the variable.

A polynomial is a mathematical expression that contains variables and coefficients and is formed by using addition, subtraction, and multiplication operations. The variables in a polynomial are raised to whole-number exponents, and the coefficients can be any real number.

Some examples of Polynomials:

• 2x − 1 is a polynomial in variable x.
• 2x² + 2x + 1 is a polynomial in variable y.

Note: Expressions like 3x²+2√x+4, 1 / (x²+2x+1), and 3x³+2/x+4 are not polynomials because negative exponents, fractional exponents, radicals, and division by a variable are all prohibited in polynomials.

Degree of Polynomials

The highest exponent of the variable in the algebraic expression is called Degree of a Polynomial.

Some examples of the degree of polynomials:

• 2x² + 3x +1 is a polynomials of degree 2 in the variable x.
• 3y³ + 2y² + 4y + 1 is a polynomials of degree 3 in the variable y.

Types of Polynomials

Various types of Polynomials based on the number of terms that the polynomial has been,

Types	Definition	Representation	Example
Constant Polynomials	A polynomial of degree Zero	f(x) = k	f(x) = 2
Linear Polynomials	A polynomial of degree One	g(x) = ax + b, a ≠ 0	g(x) = 2x + 1
Quadratic Polynomials	A polynomial of degree Two	h(x) = ax2 + bx + c, a ≠ 0	h(x) = 2x2 − 2x + 4
Cubic Polynomials	A polynomial of degree Three	p(x) = ax3 + bx2 + cx + d, a ≠ 0	p(x) = 3x3 + 4x2 + 5x + 2
Bi-Quadratic Polynomials	A polynomial of degree Four	q(x) = ax4 + bx3 + cx2 + dx + e, a ≠ 0	q(x) = 5x4 + 3x3 + 2x2 + 4x + 1

Value of a Polynomials

If p(x) is a polynomial in x, and if k is any real number, then the value obtained by replacing x by k in p(x), is called the value of p(x) at x = k, and is denoted by p(k).

Example: What is the value of p(x) = 2x² − 3x + 1 at x = 2?

Substitute 2 for x in p(x)

p(2) = 2(2)² − 3(2) + 1

       = 8 − 6 + 1

       = 3

Therefore, the value of p(x) at x = 2 is 3.

Zeros of a Polynomial

We say that x = a is the zero of the polynomial if P(x) = 0 at that point. The process of finding zero is basically the process of finding out the solutions of any polynomial equation.

Example: Find the zeros of the quadratic polynomial f(x) = x² + 7x + 12.

Solution:

First, find the factor of x² + 7x +12.

x² + 7x + 12 = x² + (4 + 3)x + 12

                    = x² + 4x +3x + 12

                    = x (x + 4) + 3 (x + 4)

                    = (x + 3)(x + 4)

So, f(x) = (x + 3)(x + 4)

Zeros of polynomial f(x) are given by f(x) = 0.

(x + 3)(x + 4) = 0

x = −4 or x = −3

Therefore, the zeros of f(x) are −4 and −3.

Geometrical Meaning of Zeros of Polynomial

The geometrical meaning of the zeros of a polynomial is shown below:

• In general, for a linear polynomial ax + b, a ≠ 0, the graph of y = ax + b is a straight line that intersects the x-axis at exactly one point, namely, (−b / a, 0)
• Geometrically that a quadratic polynomial can have either two distinct zeroes or two equal zeroes (i.e., one zero), or no zero. This also means that a polynomial of degree 2 has at most two zeroes.

Possibilities of Quadratic Polynomial	Graphically Representation
Quadratic polynomial is factorizable into two distinct linear factors
Quadratic polynomial is factorizable into two equal linear factors
Quadratic polynomial is not factorizable

Note: The graph of the quadratic polynomial is always a parabola either opening upwards or opening downwards.

• The graph of the cubic polynomial will always cross the x-axis at least once and at most thrice.

Note: A polynomial p(x) of degree n crosses the x-axis at most ‘n’ points and can have a maximum of n zeros.

Relationship between Zeros and Coefficient of a Polynomial

The relationship between zeros and coefficient of a polynomial is shown below:

Type of polynomial	Number of zeros	General form	Relationship between zeros and coefficient of a polynomial
Linear	1	ax + b, a ≠ 0	k = −b / a
Quadratic	2	ax2 + bx + c, a ≠ 0	Sum of zeros (α + β) = −b / a
			Product of zeros (αβ) = c / a
Cubic	3	ax3 + bx2 + cx + d, a ≠ 0	Sum of zeros (α + β + γ) = −b / a
			Product of zeros (αβγ) = −d / a
			Sum of the product of zeros taken 2 at a time (αβ + βγ + αγ) = c / a

Derivations for Zeros and Coefficient of Quadratic Polynomial

Let us assume α and β represents the zeros of quadratic polynomial f(x) = ax² + bx + c.

Use the factor theorem, (x − α) and (x − β) are the factor of f(x).

f(x) = k(x − α)(x − β)

where k is a constant.

ax² + bx + c = k(x² − (α + β)x + αβ)

ax² + bx + c = kx² − kx(α + β) + kαβ

Now compare the Coefficient, we get

• a = k
• b = −k(α + β)
• c = kαβ

So using the above values we get,

• Sum of the roots = (α + β) = −b/a
• Product of the roots (αβ) = c/a

Derivations for Zeros and Coefficient of Cubic Polynomial

Let us assume α, β, and γ represents the zeros of cubic polynomial f(x) = ax³ + bx² + cx + d.

Use the factor theorem, (x − α), (x − β), and (x − γ) are the factor of f(x).

f(x) = k(x − α)(x − β)(x − γ)

where k is a constant.

ax³ + bx³ + cx + d = k(x² − (α + β)x + αβ)(x − γ)

ax³ + bx² + cx + d = kx³ −kx²γ − kx²(α + β) +  kγ(α + β)x + kαβx − kαβγ

Compare the coefficient, we get

• a = k
• b = −k(α + β + γ)
• c = k(αβ + βγ + αγ)
• d = −kαβγ

So using the above values we get,

• Sum of the Roots (α + β + γ) = −b/ a
• Sum of Roots two at a time (αβ + βγ + αγ) = c / a
• Product of the roots (αβγ) = −d/ a

Example 1: If α and β are the zeros of the polynomials 2x² − 4x + 5, then find the value of α² + β².

Solution:

Sum of zeros (α + β) = −(−4) / 2

                                 = 2

Product of zeros (αβ) = 5 / 2

Use the algebraic identity,

(a + b)² = a² + b² +2ab

(α + β)² = α² + β² + 2αβ

Substitute 2 for α + β and 5 / 2 for αβ in the above equation.

2² = α² + β² + 2 × (5 / 2)

4  =  α² + β² + 5

α² + β² = −1

Therefore, the value of α² + β² is −1.

Example 2: If α, β, and γ are the zeros of the polynomials 6x³ + 3x³ + −5x + 1, then find the value of α^-1 + β^-1 + γ^-1.

Solution:

Product of Zeros (αβγ) = −1 / 6

Sum of Product of Zeros taken 2 at a time (αβ + βγ + αγ) = −5 / 6

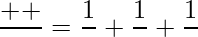
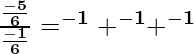
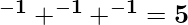
Division Algorithm for Polynomial

The division algorithm for polynomials is a method for dividing one polynomial by another. It is similar to the long division algorithm for integers but with some key differences. We can perform the division of polynomials using various steps that are,

Step 1: The first step is to write the dividend and divisor in decreasing order of their degrees. The dividend is the polynomial that is being divided, and the divisor is the polynomial that is doing the dividing.

Step 2: Next, we need to find the first term of the quotient. This is done by dividing the leading term of the dividend by the leading term of the divisor. The result is the first term of the quotient, and it is placed above the bar.

Step 3: Now, we need to subtract the product of the first term of the quotient and the divisor from the dividend. This gives us a new polynomial, which is called the remainder.

Step 4: If the degree of the remainder is less than the degree of the divisor, then we are finished. The quotient is the polynomial with the first term that we found, and the remainder is the polynomial that we just subtracted.

Step 5: If the degree of the remainder is equal to the degree of the divisor, then we need to repeat the process. We find the next term of the quotient by dividing the leading term of the remainder by the leading term of the divisor. We then subtract the product of the new term of the quotient and the divisor from the remainder. We continue this process until the degree of the remainder is less than the degree of the divisor.

The division algorithm for polynomials can be used to solve a variety of problems, such as finding the roots of a polynomial and finding the inverse of a polynomial.

Example: Divide the polynomial f(x) = 3x² − x³ − 3x + 5 by the polynomial g(x) = x − 1 − x² and verify the division algorithm.

Solution:

Rewrite the given polynomial in standard form.

f(x) = -x³ + 3x² – 3x + 5 and g(x) = -x² + x – 1

Use the long division method,

So, the remainder r(x) is 3.

Quotient × Divisor + Remainder = (x − 2)(−x² + x − 1) + 3

−x³ + x² − x + 2x² −2x +2 + 3

−x³ + 3x² − 3x + 5  (Dividend)

Hence, the division algorithm, is verified.

FAQs on Polynomial Class 10 Notes Chapter 4

Q1: What is a Polynomial?

Answer:

A polynomial is an algebraic expression consisting of variables, coefficients, and exponents, that can be added, subtracted, multiplied and divided.

Q2: What are Different Types of Polynomials?

Answer:

There are several types of polynomials, including monomials, binomials, trinomials, quadrinomials, and so on, based on the number of terms in the expression.

Q3: What is the Degree of a Polynomial?

Answer:

The degree of a polynomial is the highest power of the variable in the expression. For example, in the polynomial 

3x² + 4x + 1

The degree of the polynomial is 2.

Q4: What are Zeros of a Polynomial?

Answer:

Zeros of a polynomial are the values of the variable that make the polynomial equal to zero. These are also called roots or solutions of the polynomial.

Q5: What is the Factor Theorem?

Answer:

The factor theorem states that if a polynomial f(x) has a factor (x-a), then f(a) = 0.

Q6: What is the Remainder Theorem?

Answer:

The remainder theorem states that if a polynomial f(x) is divided by a linear polynomial (x-a), then the remainder is equal to f(a).

Q7: What are Algebraic Identities of Polynomials?

Answer:

Algebraic identities related to polynomials are formulas that help in the simplification and evaluation of polynomials. Examples of such identities include 

• (a + b)² = a² + 2ab + b²
• (a – b)² = a² – 2ab + b²

Q8: How can I Solve Problems related to Polynomials?

Answer:

To solve problems related to polynomials, it is important to understand the concepts and formulas related to polynomials. Practice solving different types of problems and equations related to polynomials, and refer to textbooks and study materials for guidance. You can also seek help from your teacher or tutor if you are having difficulty with a particular concept.