Pentadecagonal Number
Last Updated :
19 Sep, 2022
Given a number N, the task is to find the Nth Pentadecagonal number.
A Pentadecagonal number is a figurate number that extends the concept of triangular and square numbers to the pentadecagon(a 15-sided polygon). The Nth pentadecagonal number counts the number of dots in a pattern of N nested pentadecagons, all sharing a common corner, where the ith tridecagon in the pattern has sides made of ‘i’ dots spaced one unit apart from each other. The first few Pentadecagonal numbers are 1, 15, 42, 82, 135, 201, 280 …
Examples:
Input: N = 2
Output: 15
Explanation:
The second Pentadecagonal number is 15.
Input: N = 6
Output: 201

Approach: The Nth Pentadecagonal number is given by the formula:
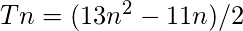
Below is the implementation of the above approach:
C++
#include <bits/stdc++.h>
using namespace std;
int Pentadecagonal_num(int n)
{
return (13 * n * n - 11 * n) / 2;
}
int main()
{
int n = 3;
cout << Pentadecagonal_num(n) << endl;
n = 10;
cout << Pentadecagonal_num(n) << endl;
return 0;
}
|
Java
import java.io.*;
import java.util.*;
class GFG{
static int Pentadecagonal_num(int n)
{
return (13 * n * n - 11 * n) / 2;
}
public static void main(String[] args)
{
int n = 3;
System.out.println(Pentadecagonal_num(n));
n = 10;
System.out.println(Pentadecagonal_num(n));
}
}
|
Python3
def Pentadecagonal_num(n):
return (13 * n * n - 11 * n) / 2
n = 3
print(int(Pentadecagonal_num(n)))
n = 10
print(int(Pentadecagonal_num(n)))
|
C#
using System;
class GFG{
static int Pentadecagonal_num(int n)
{
return (13 * n * n - 11 * n) / 2;
}
public static void Main(string[] args)
{
int n = 3;
Console.Write(Pentadecagonal_num(n) + "\n");
n = 10;
Console.Write(Pentadecagonal_num(n) + "\n");
}
}
|
Javascript
<script>
function Pentadecagonal_num(n)
{
return (13 * n * n - 11 * n) / 2;
}
let n = 3;
document.write(Pentadecagonal_num(n) + "</br>");
n = 10;
document.write(Pentadecagonal_num(n));
</script>
|
Time complexity: O(1) as it is doing constant operations
Auxiliary space: O(1) as it is using constant space for variables
Reference: https://en.wikipedia.org/wiki/Polygonal_number
Share your thoughts in the comments
Please Login to comment...