Parameters for Feature Selection
Last Updated :
29 Apr, 2018
Prerequisite :
Introduction to Dimensionality Reduction
Dimensionality reduction is the process of reducing the number of random variables under consideration, by obtaining a set of principal variables. It can be divided into
feature selection and
feature extraction.
Dimensionality Reduction is an important factor in predictive modeling. Various proposed methods have introduced different approaches to do so by either graphically or by various other methods like filtering, wrapping or embedding. However, most of these approaches are based on some threshold values and benchmark algorithms that determine the optimality of the features in the dataset.
One motivation for dimensionality reduction is that higher dimensional data sets increase the time complexity and also the space required will be more. Also, all the features in the dataset might not be useful. Some may contribute no information at all, while some may contribute similar information as the other features. Selecting the optimal set of features will help us hence reduce the space and time complexity as well as increase the accuracy or purity of classification (or regression) and clustering (or association) for supervised and unsupervised learning respectively.
Feature selection has four different approaches such as filter approach, wrapper approach, embedded approach, and hybrid approach.
- Wrapper approach :
This approach has high computational complexity. It uses a learning algorithm to evaluate the accuracy produced by the use of the selected features in classification. Wrapper methods can give high classification accuracy for particular classifiers.
- Filter approach :
A subset of features is selected by this approach without using any learning algorithm. Higher-dimensional datasets use this method and it is relatively faster than the wrapper-based approaches.
- Embedded approach :
The applied learning algorithms determine the specificity of this approach and it selects the features during the process of training the data set.
- Hybrid approach :
Both filter and wrapper-based methods are used in hybrid approach. This approach first selects the possible optimal feature set which is further tested by the wrapper approach. It hence uses the advantages of both filter and wrapper-based approach.
Parameters For Feature Selection :
The parameters are classified based on two factors –
The Similarity of information contributed by the features :
1. CORRELATION
The features are classified as associated or similar mostly based on their correlation factor. In the data set, we have many features which are correlated. Now the problem with having correlated features is that, if f1 and f2 are two correlated features of a data set, then the classifying or regression model including both f1 and f2 will give the same as the predictive model compared to the scenario where either f1 or f2 was included in the dataset. This is because both f1 and f2 are correlated and hence they contribute the same information regarding the model in the data set. There are various methods to calculate the correlation factor, however, Pearson’s correlation coefficient is most widely used. The formula for Pearson’s correlation coefficient(
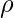
) is:

where
cov(X, Y) - covariance
sigma(X) - standard deviation of X
sigma(Y) - standard deviation of Y
Thus, the correlated features are irrelevant, as they all contribute similar information. Only one representative of the whole correlated or associated features would give the same classification or regression outcome. Hence these features are redundant and excluded for dimensionality reduction purposes after selecting a particular representative from each associated or correlated group of features using various algorithms.
Quantum of information contributed by the features :
1. ENTROPY
Entropy is the measure of the average information content. The higher the entropy, the higher is the information contribution by that feature. Entropy (H) can be formulated as:
![Rendered by QuickLaTeX.com {\displaystyle \mathrm {H} (X)=\mathrm {E} [\mathrm {I} (X)]=\mathrm {E} [-\ln(\mathrm {P} (X))]\newline}](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-f650ef4f9f18304bf852a159f8548947_l3.png)
where
X - discrete random variable X
P(X) - probability mass function
E - expected value operator,
I - information content of X.
I(X) - a random variable.
In Data Science, entropy of a feature f1 is calculated by excluding feature f1 and then calculating the entropy of the rest of the features. Now, the lower the entropy value (excluding f1) the higher will be the information content of f1. In this manner the entropy of all the features is calculated. At the end, either a threshold value or further relevancy check determines the optimality of the features on the basis of which features are selected. Entropy is mostly used for Unsupervised Learning as we do have a class field in the dataset and hence entropy of the features can give substantial information.
2. MUTUAL INFORMATION
In information theory, mutual information I(X;Y) is the amount of uncertainty in X due to the knowledge of Y. Mathematically, mutual information is defined as

where
p(x, y) - joint probability function of X and Y,
p(x) - marginal probability distribution function of X
p(y) - marginal probability distribution function of Y
Mutual Information in Data science is mostly calculated to know the amount of information shared about the class by a feature. Hence is mostly used for dimensionality reduction in
Supervised Learning. The features which have high mutual information value corresponding to the class in a supervised learning are considered optimal since they can influence the predictive model towards the right prediction and hence increase the accuracy of the model.
Reference : http://www.cs.uccs.edu/~jkalita/papers/2014/HoqueExpertSystems2014.pdf
Share your thoughts in the comments
Please Login to comment...