Number of loops of size k starting from a specific node
Last Updated :
14 Sep, 2022
Given two positive integer n, k. Consider an undirected complete connected graph of n nodes in a complete connected graph. The task is to calculate the number of ways in which one can start from any node and return to it by visiting K nodes.
Examples:
Input : n = 3, k = 3
Output : 2

Input : n = 4, k = 2
Output : 3
Lets f(n, k) be a function which return number of ways in which one can start from any node and return to it by visiting K nodes.
If we start and end from one node, then we have K – 1 choices to make for the intermediate nodes since we have already chosen one node in the beginning. For each intermediate choice, you have n – 1 options. So, this will yield (n – 1)k – 1 but then we have to remove all the choices cause smaller loops, so we subtract f(n, k – 1).
So, recurrence relation becomes,
f(n, k) = (n - 1)k - 1 - f(n, k - 1) with base case f(n, 2) = n - 1.
On expanding,
f(n, k) = (n - 1)k - 1 - (n - 1)k - 2 + (n - 1)k - 3 ..... (n - 1) (say eqn 1)
Dividing f(n, k) by (n - 1),
f(n, k)/(n - 1) = (n - 1)k - 2 - (n - 1)k - 3 + (n - 1)k - 4 ..... 1 (say eqn 2)
On adding eqn 1 and eqn 2,
f(n, k) + f(n, k)/(n - 1) = (n - 1)k - 1 + (-1)k
f(n, k) * ( (n -1) + 1 )/(n - 1) = (n - 1)k - 1 + (-1)k
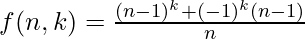
Below is the implementation of this approach:
C++
#include <bits/stdc++.h>
using namespace std;
int numOfways(int n, int k)
{
int p = 1;
if (k % 2)
p = -1;
return (pow(n - 1, k) + p * (n - 1)) / n;
}
int main()
{
int n = 4, k = 2;
cout << numOfways(n, k) << endl;
return 0;
}
|
Java
public class GFG {
static int numOfways(int n, int k)
{
int p = 1;
if (k % 2 != 0)
p = -1;
return (int)(Math.pow(n - 1, k)
+ p * (n - 1)) / n;
}
public static void main(String args[])
{
int n = 4, k = 2;
System.out.println(numOfways(n, k));
}
}
|
Python3
def numOfways(n,k):
p = 1
if (k % 2):
p = -1
return (pow(n - 1, k) +
p * (n - 1)) / n
n = 4
k = 2
print (numOfways(n, k))
|
C#
using System;
class GFG {
static int numOfways(int n, int k)
{
int p = 1;
if (k % 2 != 0)
p = -1;
return (int)(Math.Pow(n - 1, k)
+ p * (n - 1)) / n;
}
static void Main()
{
int n = 4, k = 2;
Console.Write( numOfways(n, k) );
}
}
|
PHP
<?php
function numOfways( $n, $k)
{
$p = 1;
if ($k % 2)
$p = -1;
return (pow($n - 1, $k) +
$p * ($n - 1)) / $n;
}
$n = 4;
$k = 2;
echo numOfways($n, $k);
?>
|
Javascript
<script>
function numOfways(n, k)
{
let p = 1;
if (k % 2 != 0)
p = -1;
return (Math.pow(n - 1, k)
+ p * (n - 1)) / n;
}
let n = 4, k = 2;
document.write(numOfways(n, k));
</script>
|
Share your thoughts in the comments
Please Login to comment...