Number of nodes greater than a given value in n-ary tree
Last Updated :
13 Mar, 2023
Given a n-ary tree and a number x, find and return the number of nodes which are greater than x.
Example:
In the given tree, x = 7
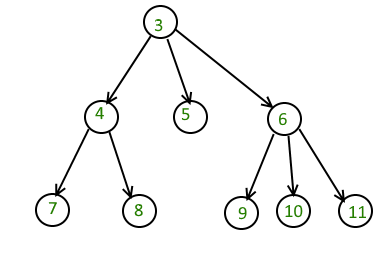
Number of nodes greater than x are 4.
Approach: The idea is maintain a count variable initialize to 0. Traverse the tree and compare root data with x. If root data is greater than x, increment the count variable and recursively call for all its children.
Below is the implementation of idea.
C++
#include <bits/stdc++.h>
using namespace std;
struct Node {
int key;
vector<Node*> child;
};
Node* newNode(int key)
{
Node* temp = new Node;
temp->key = key;
return temp;
}
int nodesGreaterThanX(Node* root, int x)
{
if (root == NULL)
return 0;
int count = 0;
if (root->key > x)
count++;
int numChildren = root->child.size();
for (int i = 0; i < numChildren; i++) {
Node* child = root->child[i];
count += nodesGreaterThanX(child, x);
}
return count;
}
int main()
{
Node* root = newNode(5);
(root->child).push_back(newNode(1));
(root->child).push_back(newNode(2));
(root->child).push_back(newNode(3));
(root->child[0]->child).push_back(newNode(15));
(root->child[1]->child).push_back(newNode(4));
(root->child[1]->child).push_back(newNode(5));
(root->child[2]->child).push_back(newNode(6));
int x = 5;
cout << "Number of nodes greater than "
<< x << " are ";
cout << nodesGreaterThanX(root, x)
<< endl;
return 0;
}
|
Java
import java.util.*;
class Node{
int key;
ArrayList<Node> child;
Node(int val)
{
key = val;
child = new ArrayList<>();
}
}
class GFG{
public static int nodesGreaterThanX(Node root, int x)
{
if (root == null)
return 0;
int count = 0;
if (root.key > x)
count++;
for(Node child : root.child)
{
count += nodesGreaterThanX(child, x);
}
return count;
}
public static void main(String[] args)
{
Node root = new Node(5);
root.child.add(new Node(1));
root.child.add(new Node(2));
root.child.add(new Node(3));
root.child.get(0).child.add(new Node(15));
root.child.get(1).child.add(new Node(4));
root.child.get(1).child.add(new Node(5));
root.child.get(2).child.add(new Node(6));
int x = 5;
System.out.print("Number of nodes greater than " +
x + " are ");
System.out.println(nodesGreaterThanX(root, x));
}
}
|
Python3
class Node:
def __init__(self, data):
self.key = data
self.child = []
def nodesGreaterThanX(root: Node, x: int) -> int:
if root is None:
return 0
count = 0
if root.key > x:
count += 1
numChildren = len(root.child)
for i in range(numChildren):
child = root.child[i]
count += nodesGreaterThanX(child, x)
return count
if __name__ == "__main__":
ans = 0
k = 25
root = Node(5)
(root.child).append(Node(1))
(root.child).append(Node(2))
(root.child).append(Node(3))
(root.child[0].child).append(Node(15))
(root.child[1].child).append(Node(4))
(root.child[1].child).append(Node(5))
(root.child[2].child).append(Node(6))
x = 5
print("Number of nodes greater than % d are % d" %
(x, nodesGreaterThanX(root, x)))
|
C#
using System;
using System.Collections.Generic;
public class Node
{
public int key;
public List<Node> child;
public Node(int val)
{
key = val;
child = new List<Node>();
}
}
class GFG{
public static int nodesGreaterThanX(Node root, int x)
{
if (root == null)
return 0;
int count = 0;
if (root.key > x)
count++;
foreach(Node child in root.child)
{
count += nodesGreaterThanX(child, x);
}
return count;
}
public static void Main(String[] args)
{
Node root = new Node(5);
root.child.Add(new Node(1));
root.child.Add(new Node(2));
root.child.Add(new Node(3));
root.child[0].child.Add(new Node(15));
root.child[1].child.Add(new Node(4));
root.child[1].child.Add(new Node(5));
root.child[2].child.Add(new Node(6));
int x = 5;
Console.Write("Number of nodes greater than " +
x + " are ");
Console.WriteLine(nodesGreaterThanX(root, x));
}
}
|
Javascript
class Node {
constructor(key) {
this.key = key;
this.child = [];
}
}
function newNode(key) {
return new Node(key);
}
function nodesGreaterThanX(root, x) {
if (root == null)
return 0;
let count = 0;
if (root.key > x)
count++;
const numChildren = root.child.length;
for (let i = 0; i < numChildren; i++) {
const child = root.child[i];
count += nodesGreaterThanX(child, x);
}
return count;
}
const root = newNode(5);
root.child.push(newNode(1));
root.child.push(newNode(2));
root.child.push(newNode(3));
root.child[0].child.push(newNode(15));
root.child[1].child.push(newNode(4));
root.child[1].child.push(newNode(5));
root.child[2].child.push(newNode(6));
const x = 5;
console.log("Number of nodes greater than " + x + " are " + nodesGreaterThanX(root, x));
|
Output
Number of nodes greater than 5 are 2
Time complexity: O(n) where n is the number of nodes in the binary tree.
Auxiliary Space: O(h) where h is the height of the binary tree.
Share your thoughts in the comments
Please Login to comment...