Nuclear Energy – Definition, Types, Applications
Last Updated :
25 Feb, 2024
Nuclear energy, also known as atomic energy, is the energy released in large quantities by operations that influence atomic nuclei, the dense centres of atoms. It differs from the energy of other atomic phenomena like typical chemical reactions, which solely involve atoms’ orbital electrons. Controlled nuclear fission in reactors, which are currently used to generate electricity in many parts of the globe, is one means of releasing nuclear energy. Controlled nuclear fusion, another way for getting nuclear energy, has shown promise but will not be achieved by 2020. Nuclear fusion and nuclear fission have both released massive amounts of nuclear energy.
Nuclear Energy
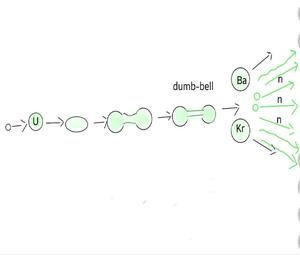
The energy obtained from the conversion of nuclear mass is known as nuclear energy. Binding energy per nucleon of light nuclei and heavy nuclei is small as compared to the binding energy per nucleon of intermediate nuclei.
When a heavy nucleus splits into two lighter nuclei then the binding energy per nucleon of light and nuclei is more than the binding energy per nucleon of the original heavy nucleus. Thus large energy is released in the process of splitting the nucleus. This process is known as nuclear fission.
For example, 1 kg of Uranium on fission gives 1014 J of energy whereas 1 kg of coal on burning gives 107 J of energy. On the other hand, when two light nuclei fuse or combine together to form a relatively heavy nucleus then the binding energy per nucleon increases. Large energy is released in the process known as nuclear fusion.
Nuclear Reactions
Atomic nuclei undergo changes as a result of nuclear reactions, which result in changes in the atom itself. Nuclear reactions change one element into something wholly other.
If a nucleus interacts with other particles and then separates without changing the properties of other nuclei, the process is referred to be nuclear scattering rather than a nuclear reaction. This has nothing to do with radioactive decay. Nuclear fusion, which happens in fissionable materials and results in induced nuclear fission, is one of the most visible nuclear reactions.
Types of Nuclear Reactions
- Inelastic scattering: When energy is transferred, this phenomenon is called inelastic scattering. It happens when the energy level is higher than the threshold. i.e.
Et = ((A+1)/A)× ε1
where Et is the inelastic threshold energy and ε1 is the first excited state’s energy.
- Elastic Scattering: Elastic Scattering happens when energy is transferred from a particle to its intended nucleus. It’s the most important step in slowing down neutrons. The entire kinetic energy of any system is preserved in the event of elastic scattering.
- Transfer Reactions: Transfer reactions are defined as the absorption of a particle followed by the emission of one or two particles.
- Capture Reactions: Capture reactions occur when nuclei capture neutral or charged particles followed by the emission of -rays. Neutron capture processes create radioactive nuclides.
Why Nuclear fusion is known as a thermonuclear reaction
Nuclear fusion cannot take place so easily. When two light nuclei are brought closer to each other, they exert a repulsive force on each other due to their positive charges. As such, these nuclei cannot fuse together. These nuclei confuse together if they have enough kinetic energy to overcome the force of repulsion between them. High kinetic energy implies a high temperature. Thus, nuclear fusion can be achieved at a very high temperature and hence is known as a thermonuclear fusion reaction. in fact, the temperature of the order of 107 K is required to trigger nuclear fusion. This much temperature is available in the core of the sun and other stars, so nuclear fusion is possible in the sun and other stars.
Applications of Nuclear Energy
- Fissionable material (Fuel): The fissionable material used in the reactor is called the fuel of the reactor. Uranium isotope(U235), Thorium isotope (Th232) and plutonium isotopes(Pu239, Pu240 and Pu241) are the most commonly used fuel in the reactor.
- Moderator: Moderator is used to slow down The fast-moving neutrons. The most commonly used moderators are graphite, water and heavy water. when heavy water is used as a moderator, then ordinary or non-enriched uranium can be used as a fuel because heavy water has more neutrons to produce fission. In the case of ordinary water as a moderator(having few electrons) enriched Uranium is used as a fuel.
- Control Material: control material is used to control the chain reaction and to maintain a stable rate of reaction. This material controls the number of neutrons available for fission. For example, cadmium rods are inserted into the core of the reactor because they can observe the neutrons. The neutrons available for fission are controlled by moving the cadmium rods in or out of the core of the reactor.
- Coolant: Coolant is a cooling material that removes the heat generated due to fission in the reactor. Commonly used coolants are water, CO2 nitrogen etc.
- Protective Shield: A protective shield in the form of a concrete thick wall surrounds the core of the reactor to save the persons working around the reactor from hazardous radiations.
Sample Problems
Question 1: Calculate the energy released in the following reaction:
3Li6 + 0n1 ⇢2He4 + 1H3
where Mass of 3Li6 =6.015126amu, Mass of 1H3 =3.016049amu, Mass of 2He4 =4.002604 amu, Mass of 0n1 =1.008665 amu.
Answer:
Total mass of reactants = 6.015126 + 1.008665 = 7.023791 amu
Total mass of products = 4.002604 + 3.016049 = 7.018653 amu
Mass difference = (7.023791 – 7.018653) = 0.005138 amu
Energy released = 0.005138 × 931 MeV = 4.783MeV.
Question 2: The nucleus of an atom is 92Y235 initially at rest, decays by emitting on α particle as per the equation:
92Y235 ⇢90X231 + 2He4 + Energy
It is given that the binding energies per nucleon of the parent and the daughter nuclei are 7.8 MeV and 7.835MeV respectively and that of α particle is 7.07 MeV/nucleon. Assuming the daughter nucleus to be formed in the unexcited state and neglecting its share in the energy of the reaction. Calculate the speed of the emitted α particle. Take the mass of α particle to be 6.68 × 10 -27 kg.
Answer:
Q = (7.835 ×231) + (7.07 × 4) – (7.8 × 235 )MeV
= 5.18 MeV
= 5.18 ×1.6 ×10-13J
This entire kinetic energy is taken by α particle as given
1/2 mv2 = 5.18 × 1.6×10-13
1/2 × 6.68 ×10-27 v2 = 5.18 × 1.6 ×10-13
v = 1.57 × 107 m/s.
Question 3: Is the fission of iron(26Fe56) into aluminium(13Al28) As given below is possible?
26Fe56 ⇢13Al28 +13Al28 +Q
Given, Mass of 26Fe56 =55.934940u and mass of 13Al28 =27.98191 u.
Answer:
Q value =mass of 26Fe56 – 2 ×mass of 13Al28
= (55.934940 – 2 ×27.98191) ×931.5 MeV/u
= -0.02892u × 931.5 MeV/u
= -26.94 MeV.
Question 4: 20 MeV energy is released per fusion reaction
1H2 +1H2 ⇢ 2He4 +0n1
Calculate the mass of 1H2 consumed in a fusion reactor of power 1 MW in 1 day.
Answer:
P =1 MW =106 W =106 Js-1
t =1 day =24 × 60 × 60 = 86400 s
Energy released in 1 day = 86400× 106 J
Energy released per fusion = 20MeV
= 20 × 1.6 ×10-13 = 3.2 × 10-12 J
Mass of 1H2 consumed in one fusion (1H2 + 1H2) = 4u
= 4 ×1.66 ×10-27 kg = 6.64 ×10-27
= 6.64 × 10-27/ 3.2 × 10-12 × 86400 ×106
= 1.79 × 10-4 kg
Question 5: Calculate the energy released when three α particles (2He4) fuse to form a carbon (6C12) nucleus, given m (2He4) = 4.002603 amu.
Solution:
2He4 ⇢ 6C12 +Q
Q = m(3 2He4) – m(6C12)
= 12.0078 – 12 = 0.007809
Energy released = 0.007809 × 931 MeV
= 7.27MeV
Share your thoughts in the comments
Please Login to comment...