Naive algorithm for Pattern Searching
Last Updated :
20 Apr, 2024
Given text string with length n and a pattern with length m, the task is to prints all occurrences of pattern in text.
Note: You may assume that n > m.
Examples:
Input: text = “THIS IS A TEST TEXT”, pattern = “TEST”
Output: Pattern found at index 10
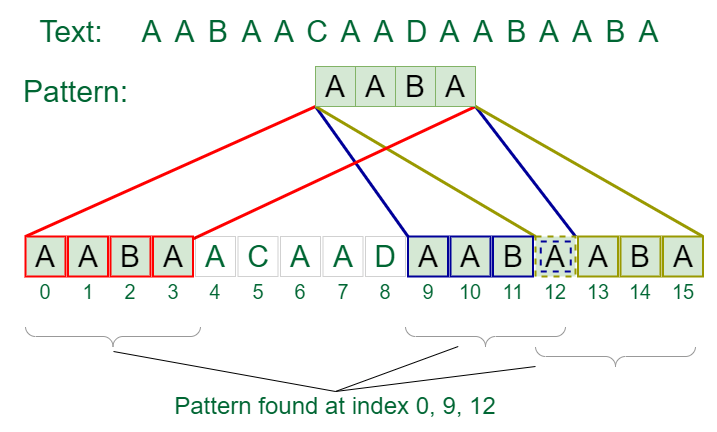
Input: text = “AABAACAADAABAABA”, pattern = “AABA”
Output: Pattern found at index 0, Pattern found at index 9, Pattern found at index 12
Pattern searching
Naive Pattern Searching algorithm:
Slide the pattern over text one by one and check for a match. If a match is found, then slide by 1 again to check for subsequent matches.
C++
#include <iostream>
#include <string>
using namespace std;
void search(string& pat, string& txt) {
int M = pat.size();
int N = txt.size();
// A loop to slide pat[] one by one
for (int i = 0; i <= N - M; i++) {
int j;
// For current index i, check for pattern match
for (j = 0; j < M; j++) {
if (txt[i + j] != pat[j]) {
break;
}
}
// If pattern matches at index i
if (j == M) {
cout << "Pattern found at index " << i << endl;
}
}
}
// Driver's Code
int main() {
// Example 1
string txt1 = "AABAACAADAABAABA";
string pat1 = "AABA";
cout << "Example 1: " << endl;
search(pat1, txt1);
// Example 2
string txt2 = "agd";
string pat2 = "g";
cout << "\nExample 2: " << endl;
search(pat2, txt2);
return 0;
}
#include <stdio.h>
#include <string.h>
void search(char* pat, char* txt) {
int M = strlen(pat);
int N = strlen(txt);
// A loop to slide pat[] one by one
for (int i = 0; i <= N - M; i++) {
int j;
// For current index i, check for pattern match
for (j = 0; j < M; j++) {
if (txt[i + j] != pat[j]) {
break;
}
}
// If pattern matches at index i
if (j == M) {
printf("Pattern found at index %d\n", i);
}
}
}
int main() {
// Example 1
char txt1[] = "AABAACAADAABAABA";
char pat1[] = "AABA";
printf("Example 1:\n");
search(pat1, txt1);
// Example 2
char txt2[] = "agd";
char pat2[] = "g";
printf("\nExample 2:\n");
search(pat2, txt2);
return 0;
}
public class PatternSearch {
public static void search(String pat, String txt) {
int M = pat.length();
int N = txt.length();
// A loop to slide pat[] one by one
for (int i = 0; i <= N - M; i++) {
int j;
// For current index i, check for pattern match
for (j = 0; j < M; j++) {
if (txt.charAt(i + j) != pat.charAt(j)) {
break;
}
}
// If pattern matches at index i
if (j == M) {
System.out.println("Pattern found at index " + i);
}
}
}
public static void main(String[] args) {
// Example 1
String txt1 = "AABAACAADAABAABA";
String pat1 = "AABA";
System.out.println("Example 1:");
search(pat1, txt1);
// Example 2
String txt2 = "agd";
String pat2 = "g";
System.out.println("\nExample 2:");
search(pat2, txt2);
}
}
def search_pattern(pattern, text):
# Get the lengths of the pattern and the text
m = len(pattern)
n = len(text)
# A loop to slide pattern over text one by one
for i in range(n - m + 1):
# For current index i, check for pattern match
j = 0
while j < m and text[i + j] == pattern[j]:
j += 1
# If the entire pattern matches the text starting at index i
if j == m:
print(f"Pattern found at index {i}")
# Example usage
if __name__ == "__main__":
# Example 1
text1 = "AABAACAADAABAABA"
pattern1 = "AABA"
print("Example 1:")
search_pattern(pattern1, text1)
# Example 2
text2 = "agd"
pattern2 = "g"
print("\nExample 2:")
search_pattern(pattern2, text2)
using System;
class PatternSearch
{
static void Search(string pat, string txt)
{
int M = pat.Length;
int N = txt.Length;
// A loop to slide pat[] one by one
for (int i = 0; i <= N - M; i++)
{
int j;
// For current index i, check for pattern match
for (j = 0; j < M; j++)
{
if (txt[i + j] != pat[j])
{
break;
}
}
// If pattern matches at index i
if (j == M)
{
Console.WriteLine($"Pattern found at index {i}");
}
}
}
static void Main()
{
// Example 1
string txt1 = "AABAACAADAABAABA";
string pat1 = "AABA";
Console.WriteLine("Example 1:");
Search(pat1, txt1);
// Example 2
string txt2 = "agd";
string pat2 = "g";
Console.WriteLine("\nExample 2:");
Search(pat2, txt2);
}
}
function search(pat, txt) {
const M = pat.length;
const N = txt.length;
// A loop to slide pat[] one by one
for (let i = 0; i <= N - M; i++) {
let j = 0;
// For current index i, check for pattern match
while (j < M && txt[i + j] === pat[j]) {
j++;
}
// If pattern matches at index i
if (j === M) {
console.log(`Pattern found at index ${i}`);
}
}
}
// Example 1
const txt1 = "AABAACAADAABAABA";
const pat1 = "AABA";
console.log("Example 1:");
search(pat1, txt1);
// Example 2
const txt2 = "agd";
const pat2 = "g";
console.log("\nExample 2:");
search(pat2, txt2);
function search($pat, $txt) {
$M = strlen($pat);
$N = strlen($txt);
// A loop to slide pat[] one by one
for ($i = 0; $i <= $N - $M; $i++) {
$j = 0;
// For current index i, check for pattern match
while ($j < $M && $txt[$i + $j] === $pat[$j]) {
$j++;
}
// If pattern matches at index i
if ($j == $M) {
echo "Pattern found at index $i\n";
}
}
}
// Example 1
$txt1 = "AABAACAADAABAABA";
$pat1 = "AABA";
echo "Example 1:\n";
search($pat1, $txt1);
// Example 2
$txt2 = "agd";
$pat2 = "g";
echo "\nExample 2:\n";
search($pat2, $txt2);
OutputPattern found at index 0
Pattern found at index 9
Pattern found at index 13
Time Complexity: O(N2)
Auxiliary Space: O(1)
Complexity Analysis of Naive algorithm for Pattern Searching:
Best Case: O(n)
- When the pattern is found at the very beginning of the text (or very early on).
- The algorithm will perform a constant number of comparisons, typically on the order of O(n) comparisons, where n is the length of the pattern.
Worst Case: O(n2)
- When the pattern doesn’t appear in the text at all or appears only at the very end.
- The algorithm will perform O((n-m+1)*m) comparisons, where n is the length of the text and m is the length of the pattern.
- In the worst case, for each position in the text, the algorithm may need to compare the entire pattern against the text.
Share your thoughts in the comments
Please Login to comment...